This is machine translation

Translated by

Mouseover text to see original. Click the button below to return to the English version of the page.

Note: This page has been translated by MathWorks. Click here to see
To view all translated materials including this page, select Country from the country navigator on the bottom of this page.

procest

Estimate process model using time or frequency data

collapse all in page

Syntax

sys = procest(data,type)

sys = procest(data,type,'InputDelay',InputDelay)

sys = procest(data,init_sys)

sys = procest(___,opt)

[sys,offset] = procest(___)

Description

example

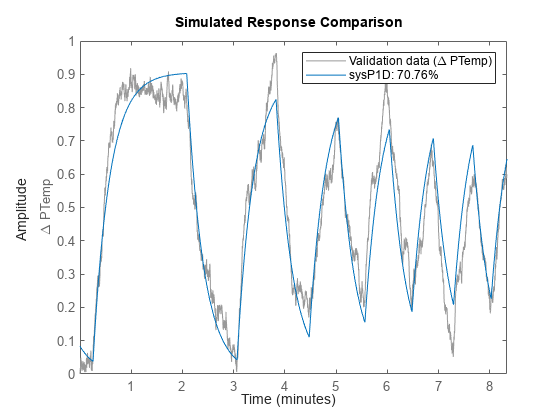
sys = procest(data,type) estimates a process model, sys, using time or frequency-domain data, data. type defines the structure of sys.

sys = procest(data,type,'InputDelay',InputDelay) specifies the input delay InputDelay.

example

sys = procest(data,init_sys) uses the process model init_sys to configure the initial parameterization.

example

sys = procest(___,opt) specifies additional model estimation options. Use opt with any of the previous syntaxes.

example

[sys,offset] = procest(___) returns the estimated value of the offset in input signal. Input offset is automatically estimated when the model contains an integrator, or when you set the InputOffset estimation option to 'estimate' using procestOptions. Use offset with any of the previous syntaxes.

Input Arguments

collapse all

`data` — Estimation data
`iddata` | `idfrd` | `frd`

Estimation data, specified as an iddata object containing the input and output signal values, for time-domain estimation. For frequency-domain estimation, data can be one of the following:

Recorded frequency response data (frd or idfrd)
iddata object with its properties specified as follows:
- InputData — Fourier transform of the input signal
- OutputData — Fourier transform of the output signal
- Domain — 'Frequency'

data must have at least one input and one output.

Time-series models, which are models that contain no measured inputs, cannot be estimated using procest. Use ar, arx, or armax for time-series models instead.

`type` — Process model structure
character vector | string | cell array of character vectors | string array

Process model structure, specified for SISO models as a character vector or string representing an acronym for the model structure, such as 'P1D' or 'P2DZ'. The acronym is made up of:

P — All 'Type' acronyms start with this letter.
0, 1, 2, or 3 — Number of time constants (poles) to be modeled. Possible integrations (poles in the origin) are not included in this number.
I — Integration is enforced (self-regulating process).
D — Time delay (dead time).
Z — Extra numerator term, a zero.
U — Underdamped modes (complex-valued poles) permitted. If U is not included in type, all poles must be real. The number of poles must be 2 or 3.

For MIMO models, use an Ny-by-Nu cell array of character vectors or string array, with one entry for each input-output pair. Here Ny is the number of inputs and Nu is the number of outputs.

For information regarding how type affects the structure of a process model, see idproc.

`InputDelay` — Input delays
`0` for all input channels (default) | numeric vector

Input delays, specified as a numeric vector specifying a time delay for each input channel. Specify input delays in the time unit stored in the TimeUnit property.

For a system with Nu inputs, set InputDelay to an Nu-by-1 vector. Each entry of this vector is a numerical value that represents the input delay for the corresponding input channel. You can also set InputDelay to a scalar value to apply the same delay to all channels.

`init_sys` — System for configuring initial parametrization
`idproc` object

System for configuring initial parametrization of sys, specified as an idproc object. You obtain init_sys by either performing an estimation using measured data or by direct construction using idproc. The software uses the parameters and constraints defined in init_sys as the initial guess for estimating sys.

Use the Structure property of init_sys to configure initial guesses and constraints for Kp, T_p1, T_p2, T_p3, T_w, Zeta, T_d, and T_z. For example:

To specify an initial guess for the T_p1 parameter of init_sys, set init_sys.Structure.Tp1.Value as the initial guess.
To specify constraints for the T_p2 parameter of init_sys:
- Set init_sys.Structure.Tp2.Minimum to the minimum T_p2 value.
- Set init_sys.Structure.Tp2.Maximum to the maximum T_p2 value.
- Set init_sys.Structure.Tp2.Free to indicate if T_p2 is a free parameter for estimation.

If opt is not specified, and init_sys was obtained by estimation, then the estimation options from init_sys.Report.OptionsUsed are used.

`opt` — Estimation options
`procestOptions` option set

Estimation options, specified as an procestOptions option set. The estimation options include:

Estimation objective
Handling on initial conditions and disturbance component
Numerical search method to be used in estimation

Output Arguments

collapse all

`sys` — Identified process model
`idproc` model

Identified process model, returned as an idproc model of a structure defined by type.

Information about the estimation results and options used is stored in the model's Report property. Report has the following fields:

Report Field Description

Status

Summary of the model status, which indicates whether the model was created by construction or obtained by estimation.

Method

Estimation command used.

InitialCondition

Handling of initial conditions during model estimation, returned as one of the following values:

'zero' — The initial conditions were set to zero.
'estimate' — The initial conditions were treated as independent estimation parameters.
'backcast' — The initial conditions were estimated using the best least squares fit.

This field is especially useful to view how the initial conditions were handled when the InitialCondition option in the estimation option set is 'auto'.

Fit

Quantitative assessment of the estimation, returned as a structure. See Loss Function and Model Quality Metrics for more information on these quality metrics. The structure has the following fields:

Field	Description
`FitPercent`	Normalized root mean squared error (NRMSE) measure of how well the response of the model fits the estimation data, expressed as a percentage.
`LossFcn`	Value of the loss function when the estimation completes.
`MSE`	Mean squared error (MSE) measure of how well the response of the model fits the estimation data.
`FPE`	Final prediction error for the model.
`AIC`	Raw Akaike Information Criteria (AIC) measure of model quality.
`AICc`	Small sample-size corrected AIC.
`nAIC`	Normalized AIC.
`BIC`	Bayesian Information Criteria (BIC).

Parameters

Estimated values of model parameters.

OptionsUsed

Option set used for estimation. If no custom options were configured, this is a set of default options. See procestOptions for more information.

RandState

State of the random number stream at the start of estimation. Empty, [], if randomization was not used during estimation. For more information, see rng in the MATLAB^® documentation.

DataUsed

Attributes of the data used for estimation. Structure with the following fields:

Field	Description
`Name`	Name of the data set.
`Type`	Data type. For `idnlarx` models, this is set to `'Time domain data'`.
`Length`	Number of data samples.
`Ts`	Sample time. This is equivalent to `Data.Ts`.
`InterSample`	Input intersample behavior. One of the following values: `'zoh'` — Zero-order hold maintains a piecewise-constant input signal between samples. `'foh'` — First-order hold maintains a piecewise-linear input signal between samples. `'bl'` — Band-limited behavior specifies that the continuous-time input signal has zero power above the Nyquist frequency. The value of `Intersample` has no effect on estimation results for discrete-time models.
`InputOffset`	Empty, `[]`, for nonlinear estimation methods.
`OutputOffset`	Empty, `[]`, for nonlinear estimation methods.

Termination

Termination conditions for the iterative search used for prediction error minimization. Structure with the following fields:

Field	Description
`WhyStop`	Reason for terminating the numerical search.
`Iterations`	Number of search iterations performed by the estimation algorithm.
`FirstOrderOptimality`	$\infty$ -norm of the gradient search vector when the search algorithm terminates.
`FcnCount`	Number of times the objective function was called.
`UpdateNorm`	Norm of the gradient search vector in the last iteration. Omitted when the search method is `'lsqnonlin'` or `'fmincon'`.
`LastImprovement`	Criterion improvement in the last iteration, expressed as a percentage. Omitted when the search method is `'lsqnonlin'` or `'fmincon'`.
`Algorithm`	Algorithm used by `'lsqnonlin'` or `'fmincon'` search method. Omitted when other search methods are used.

For estimation methods that do not require numerical search optimization, the Termination field is omitted.

For more information on using Report, see Estimation Report.

`offset` — Estimated value of input offset
vector

Estimated value of input offset, returned as a vector. When data has multiple experiments, offset is a matrix where each column corresponds to an experiment.

Examples

collapse all

Estimate a First Order Plus Dead Time Model

Open Live Script

Obtain the measured input-output data.

load iddemo_heatexchanger_data;
data = iddata(pt,ct,Ts);  
data.InputName  = '\Delta CTemp';
data.InputUnit  = 'C';
data.OutputName = '\Delta PTemp';
data.OutputUnit = 'C';
data.TimeUnit   = 'minutes';

Estimate a first-order plus dead time process model.

type = 'P1D';
sysP1D = procest(data,type);

Compare the model with the data.

compare(data,sysP1D)

Plot the model residuals.

figure
resid(data,sysP1D);

The figure shows that the residuals are correlated. To account for that, add a first order ARMA disturbance component to the process model.

opt = procestOptions('DisturbanceModel','ARMA1');
sysP1D_noise = procest(data,'p1d',opt);

Compare the models.

compare(data,sysP1D,sysP1D_noise)

Plot the model residuals.

figure
resid(data,sysP1D_noise);

The residues of sysP1D_noise are uncorrelated.

Estimate Over-parameterized Process Model Using Regularization

Open Live Script

Use regularization to estimate parameters of an over-parameterized process model.

Assume that gain is known with a higher degree of confidence than other model parameters.

Load data.

load iddata1 z1;

Estimate an unregularized process model.

m = idproc('P3UZ','K',7.5,'Tw',0.25,'Zeta',0.3,'Tp3',20,'Tz',0.02);
m1 = procest(z1,m);

Estimate a regularized process model.

opt = procestOptions;
opt.Regularization.Nominal = 'model';
opt.Regularization.R = [100;1;1;1;1];
opt.Regularization.Lambda = 0.1;
m2 = procest(z1,m,opt);

Compare the model outputs with data.

compare(z1,m1,m2);

Regularization helps steer the estimation process towards the correct parameter values.

Specify Parameter Initial Values for Estimated Process Model

Open Live Script

Estimate a process model after specifying initial guesses for parameter values and bounding them.

Obtain input/output data.

data = idfrd(idtf([10 2],[1 1.3 1.2],'iod',0.45),logspace(-2,2,256));

Specify the parameters of the estimation initialization model.

type = 'P2UZD';
init_sys = idproc(type);

init_sys.Structure.Kp.Value = 1; 
init_sys.Structure.Tw.Value = 2; 
init_sys.Structure.Zeta.Value = 0.1; 
init_sys.Structure.Td.Value = 0; 
init_sys.Structure.Tz.Value = 1; 
init_sys.Structure.Kp.Minimum = 0.1;
init_sys.Structure.Kp.Maximum = 10;
init_sys.Structure.Td.Maximum = 1;
init_sys.Structure.Tz.Maximum = 10;

Specify the estimation options.

opt = procestOptions('Display','full','InitialCondition','Zero');
opt.SearchMethod = 'lm'; 
opt.SearchOptions.MaxIterations = 100;

Estimate the process model.

sys = procest(data,init_sys,opt);

Since the 'Display' option is specified as 'full', the estimation progress is displayed in a separate Plant Identification Progress window.

Compare the data to the estimated model.

compare(data,sys,init_sys);

Detect Overparameterization of Estimated Model

Open Live Script

Obtain input/output data.

load iddata1 z1
load iddata2 z2
data = [z1 z2(1:300)];

data is a data set with 2 inputs and 2 outputs. The first input affects only the first output. Similarly, the second input affects only the second output.

In the estimated process model, the cross terms, modeling the effect of the first input on the second output and vice versa, should be negligible. If higher orders are assigned to those dynamics, their estimations show a high level of uncertainty.

Estimate the process model.

type = 'P2UZ'; 
sys = procest(data,type);

The type variable denotes a model with complex-conjugate pair of poles, a zero, and a delay.

To evaluate the uncertainties, plot the frequency response.

w = linspace(0,20*pi,100);
h = bodeplot(sys,w);
showConfidence(h);

Return Input Offsets Estimated During Process Model Estimation

Open Live Script

load iddata1
[sys,offset] = procest(z1,'P1DI');
offset

offset = 0.0412

Extended Capabilities

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

Parallel computing support is available for estimation using the lsqnonlin search method (requires Optimization Toolbox™). To enable parallel computing, use procestOptions, set SearchMethod to 'lsqnonlin', and set SearchOptions.Advanced.UseParallel to true.

For example:

opt = procestOptions;
opt.SearchMethod = 'lsqnonlin';
opt.SearchOptions.Advanced.UseParallel = true;

This is machine translation

procest

Syntax

Description

Input Arguments

`data` — Estimation data
`iddata` | `idfrd` | `frd`

`type` — Process model structure
character vector | string | cell array of character vectors | string array

`InputDelay` — Input delays
`0` for all input channels (default) | numeric vector

`init_sys` — System for configuring initial parametrization
`idproc` object

`opt` — Estimation options
`procestOptions` option set

Output Arguments

`sys` — Identified process model
`idproc` model

`offset` — Estimated value of input offset
vector

Examples

Estimate a First Order Plus Dead Time Model

Estimate Over-parameterized Process Model Using Regularization

Specify Parameter Initial Values for Estimated Process Model

Detect Overparameterization of Estimated Model

Return Input Offsets Estimated During Process Model Estimation

Extended Capabilities

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

See Also

Topics

Introduced in R2012a

System Identification Toolbox Documentation

Support

试用 MATLAB、Simulink 以及其他产品

This is machine translation

procest

Syntax

Description

Input Arguments

data — Estimation data iddata | idfrd | frd

type — Process model structure character vector | string | cell array of character vectors | string array

InputDelay — Input delays 0 for all input channels (default) | numeric vector

init_sys — System for configuring initial parametrization idproc object

opt — Estimation options procestOptions option set

Output Arguments

sys — Identified process model idproc model

offset — Estimated value of input offset vector

Examples

Estimate a First Order Plus Dead Time Model

Estimate Over-parameterized Process Model Using Regularization

Specify Parameter Initial Values for Estimated Process Model

Detect Overparameterization of Estimated Model

Return Input Offsets Estimated During Process Model Estimation

Extended Capabilities

Automatic Parallel Support Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

See Also

Topics

Introduced in R2012a

Select a Web Site

How to Get Best Site Performance

Americas

Europe

Asia Pacific

System Identification Toolbox Documentation

Support

试用 MATLAB、Simulink 以及其他产品

WeChat

`data` — Estimation data
`iddata` | `idfrd` | `frd`

`type` — Process model structure
character vector | string | cell array of character vectors | string array

`InputDelay` — Input delays
`0` for all input channels (default) | numeric vector

`init_sys` — System for configuring initial parametrization
`idproc` object

`opt` — Estimation options
`procestOptions` option set

`sys` — Identified process model
`idproc` model

`offset` — Estimated value of input offset
vector

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.