idinput
生成输入信号以支持系统辨识
语法
说明
idinput 命令为您的系统生成具有指定特性的输入信号。您可以使用生成的输入,仿真系统的响应以研究系统行为。例如,你可以研究系统对周期性输入的响应。该系统可以是实际的物理系统,也可以是模型,例如 Simulink® 模型。您还可以设计最优实验。例如,您可以确定哪些输入信号能够隔离系统中的故障或非线性问题。您还可以使用 idinput 设计具有足够带宽的输入信号,以激发系统的动态范围。
示例
生成一个单通道随机二进制输入信号,包含 200 个采样点。
N = 200; u = idinput(N);
u 是长度为 200 的列向量。u 中的值要么是 -1,要么是 1。
从生成的信号创建一个 iddata 对象。例如,在此示例中,请将采样时间设置为 1 秒。
u = iddata([],u,1);
要检查信号,请绘制信号图。
plot(u)
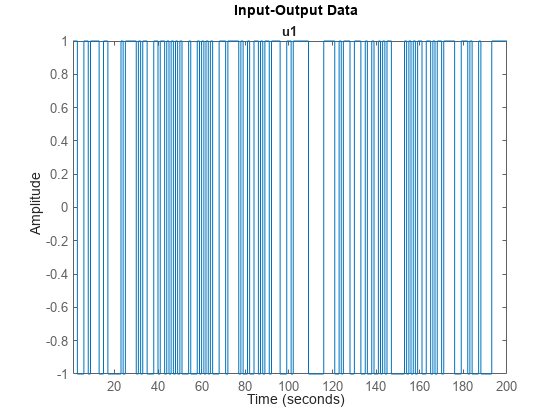
生成的信号是一个随机二进制输入信号,其值是 -1 或 1。您可以使用生成的输入信号,通过 sim 命令仿真系统的输出。
生成一个包含 200 个采样点的双通道随机二进制输入信号。
N = 200; u = idinput([N,2]);
u 是一个 200×2 的矩阵,其元素值是 -1 或 1。
从生成的信号创建一个 iddata 对象。例如,在此示例中,请将采样时间设置为 1 秒。
u = iddata([],u,1);
绘制两个通道的信号曲线,并分析这些信号。
plot(u)
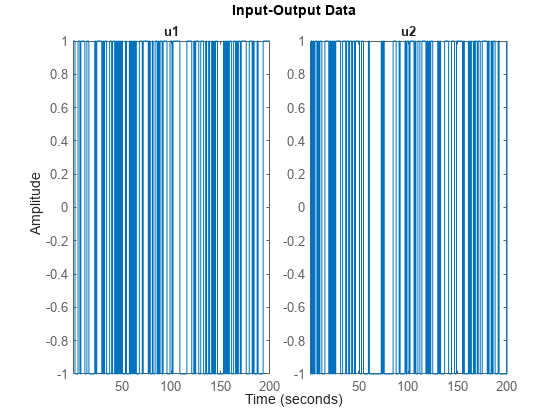
该图显示了两个生成的随机二进制信号,其值是 -1 或 1。
生成一个单通道周期性随机二进制输入信号,其周期为 10 个采样点,信号中包含 5 个周期。
NumChannel = 1; Period = 10; NumPeriod = 5; u = idinput([Period,NumChannel,NumPeriod]);
u 是长度为 50(= Period*NumPeriod)的列向量。u 中的值要么是 -1,要么是 1。
从生成的信号创建一个 iddata 对象。将采样时间设定为 1 秒。
u = iddata([],u,1);
绘制信号图。
plot(u)
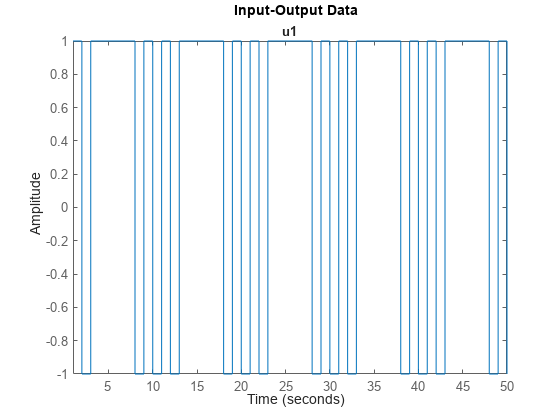
如指定,生成的单通道周期性随机二进制输入信号周期为 10 秒,信号中包含 5 个完整周期。
生成单通道周期性随机高斯输入信号,其周期为 50 个采样点,信号中包含 5 个周期。首先使用整个频率范围生成信号,然后指定通带。
NumChannel = 1;
Period = 50;
NumPeriod = 5;
u = idinput([Period,NumChannel,NumPeriod],'rgs');u 是长度为 250(= 周期数 * 周期数)的列向量。
从生成的信号创建一个 iddata 对象,并绘制该信号。例如,在此示例中,请将采样时间设置为 0.01 秒。
u = iddata([],u,0.01); plot(u)
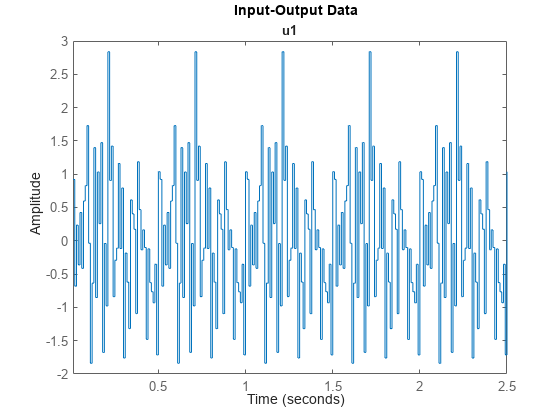
该图显示 u 包含 50 个随机采样的片段,重复了 5 次。该信号为高斯白噪声信号,均值为零,方差为一。
由于采样时间为 0.01 秒,生成的信号周期为 0.5 秒。信号的频率成分覆盖了整个可用范围 (0-50 Hz)。
现在指定一个通带,频率范围为 0 至 25 赫兹(即奈奎斯特频率的 0.5 倍)。
Band = [0 0.5];
u2 = idinput([Period,NumChannel,NumPeriod],'rgs',Band);创建一个 iddata 对象,并绘制信号。
u2 = iddata([],u2,0.01); plot(u2)
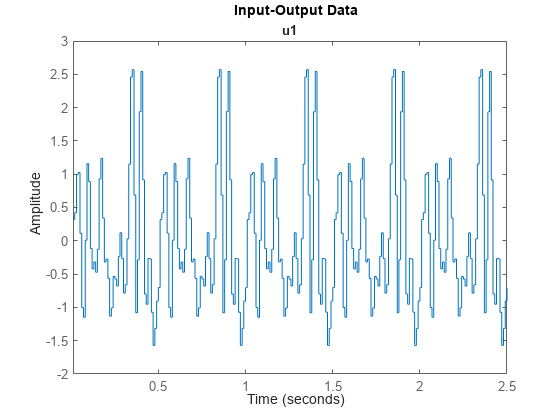
生成的信号 u2 的频率成分限制在 0-25 赫兹范围内。
伪随机二进制输入信号 (PRBS) 是一种确定性信号,其频率属性模拟白噪声。伪随机比特序列 (PRBS) 本质上具有周期性,其最大周期长度为 ,其中整数 n 为该 PRBS 的阶数。有关详细信息,请参阅伪随机二进制信号。
指定单通道伪随机比特序列 (PRBS) 值在 -2 和 2 之间切换。
Range = [-2,2];
将信号的时钟周期指定为 1 个采样点。也就是说,信号值可以在每个时间步长发生变化。对于伪随机二进制序列 (PRBS) 信号,时钟周期由 Band = [0 B] 指定,其中 B 是所需时钟周期的倒数。
Band = [0 1];
生成一个长度为 100 个采样点的非周期伪随机序列。
u = idinput(100,'prbs',Band,Range);Warning: The PRBS signal delivered is the 100 first values of a full sequence of length 127.
PRBS 具有固有的周期性。为生成非周期信号,软件生成一个长度为 127 的最大长度伪随机二进制序列 (PRBS),其周期大于所需采样数 100。该软件返回生成的伪随机序列 (PRBS) 的前 100 个样本。此操作确保生成的信号不具有周期性,正如生成的警告所示。
从生成的信号创建一个 iddata 对象。例如,在此示例中,请将采样时间设置为 1 秒。
u = iddata([],u,1);
绘制并检查生成的信号。
plot(u);
title('Non-Periodic Signal')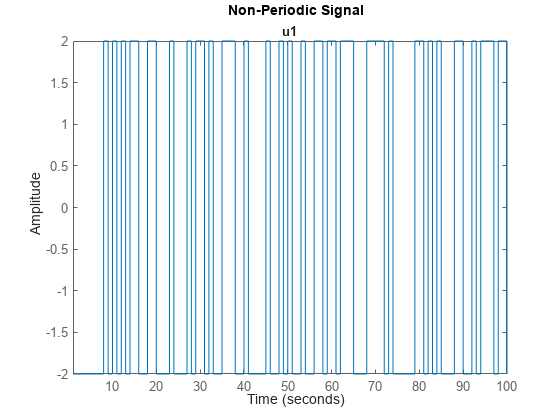
生成的信号是一个长度为 100 的非周期伪随机二进制序列,其值在 -2 和 2 之间切换。
指定伪随机二进制输入信号 (PRBS) 在 -2 和 2 之间切换。
Range = [-2,2];
将信号的时钟周期指定为 1 个采样点。也就是说,信号值可以在每个时间步长发生变化。对于伪随机二进制序列 (PRBS) 信号,时钟周期由 Band = [0 B] 指定,其中 B 是所需时钟周期的倒数。
Band = [0 1];
生成单通道、周期为 100 个采样点的伪随机比特序列 (PRBS),该信号包含 3 个周期。
u1 = idinput([100,1,3],'prbs',Band,Range);Warning: The period of the PRBS signal was changed to 63. Accordingly, the length of the generated signal will be 189.
伪随机比特序列 (PRBS) 本质上具有周期性,其最大周期长度为 ,其中整数 n 为该 PRBS 的阶数。若指定周期不等于最长 PRBS 长度,软件将调整生成信号的周期以获得整数倍的最长 PRBS 长度,并发出警告。有关最大长度伪随机序列 (PRBS) 的信息,请参阅伪随机二进制信号。在此示例中,期望周期 100 不等于最大长度伪随机比特序列 (PRBS),因此软件转而生成阶数为 n = floor(log2(Period)) = 6 的最大长度 PRBS。因此,伪随机二进制序列信号的周期为 63(= ),生成的信号长度为 189(= NumPeriod*63)。该结果已在生成的警告中显示。
从生成的信号创建一个 iddata 对象,并绘制该信号。将信号周期指定为 63 个采样点。
u1 = iddata([],u1,1,'Period',63); plot(u1) title('Periodic Signal')
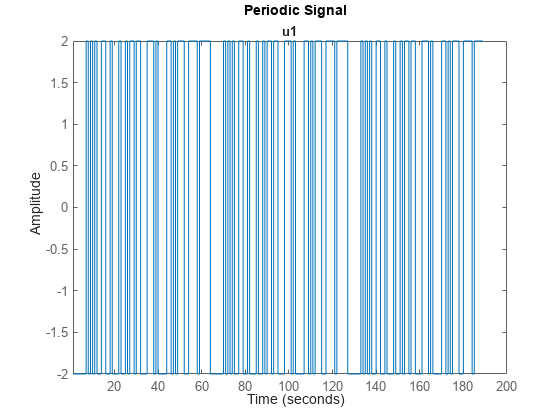
生成的信号是一个具有三个周期的周期性伪随机序列。
生成具有指定时钟周期的周期性和非周期性伪随机二进制输入信号 (PRBS)。
生成一个在 -2 和 2 之间切换的单通道伪随机二进制序列。将信号的时钟周期指定为 4 个采样点。也就是说,信号必须保持恒定至少 4 个连续采样点,才能发生变化。对于伪随机二进制序列 (PRBS) 信号,时钟周期由 Band = [0 B] 指定,其中 B 是所需时钟周期的倒数。
Range = [-2,2]; Band = [0 1/4];
首先生成一个长度为 100 的非周期信号。
u1 = idinput(100,'prbs',Band,Range);Warning: The PRBS signal delivered is the 100 first values of a full sequence of length 124.
要理解生成的警告,首先需注意该代码相当于生成一个周期为 100 个采样点、周期为 1 的单通道伪随机二进制序列 (PRBS)。
u1 = idinput([100,1,1],'prbs',Band,Range);
生成的伪随机二进制序列信号必须保持恒定至少 4 个采样点,其值才能发生变化。为满足此要求,软件首先计算出可能的最大长度伪随机比特序列 (PRBS) 的序列为 n = floor(log2(Period*B)) = 4,周期为 。有关最大长度伪随机序列 (PRBS) 的信息,请参阅伪随机二进制信号。该软件随后对该伪随机二进制序列进行拉伸处理,使得拉伸后信号的周期为 。
然而,由于该周期小于指定长度 100,软件转而计算阶数为 m = n+1 = 5 的最大长度伪随机比特序列。该软件随后将此伪随机序列拉伸,使其周期变为 。该软件将此信号的前 100 个采样值作为 u1 返回。该结果确保生成的信号并非周期性,而是在每 4 个采样点间保持恒定。
从生成的信号创建一个 iddata 对象。例如,在此示例中,请将采样时间设置为 1 秒。
u1 = iddata([],u1,1);
绘制并检查信号。
plot(u1);
title('Nonperiodic Signal')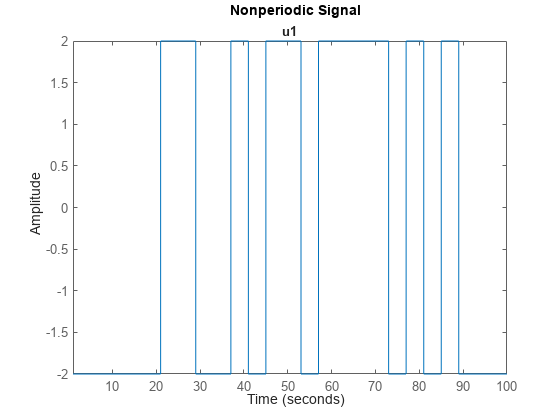
生成的信号是一个长度为 100 的非周期伪随机比特序列。每次值变化前,信号至少保持恒定 4 个采样周期。因此,该信号满足 Band 中指定的时钟周期。
现在生成一个周期为 100 个采样点、包含 3 个周期的周期信号。
u2 = idinput([100,1,3],'prbs',Band,Range);Warning: The period of the PRBS signal was changed to 60. Accordingly, the length of the generated signal will be 180.
为生成具有指定时钟周期的周期信号,软件通过将原始拉伸信号(周期为 P = 60)重复 3 次,生成 u2 信号。因此,u2 的长度为 P*NumPeriod = 60*3 = 180。生成的警告中已标明所生成信号的周期和长度变化。
从生成的信号创建一个 iddata 对象,并绘制该信号。将信号周期指定为 60 秒。
u2 = iddata([],u2,1,'Period',60); plot(u2) title('Periodic Signal')
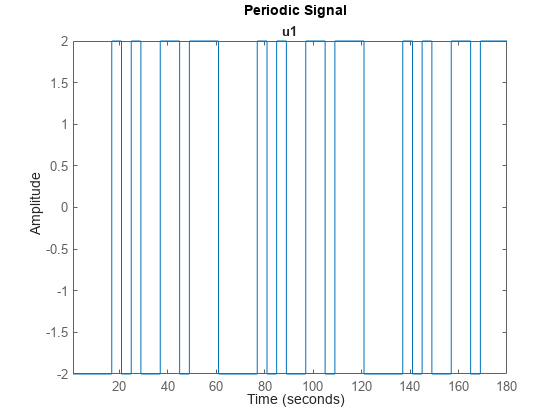
生成的信号为周期性伪随机序列,周期为 60 秒,包含 3 个周期。每次值变化前,信号至少保持恒定 4 个采样周期。因此,该信号满足规定的时钟周期。
您可以使用正弦波的默认特性生成正弦波叠加信号。或者,您可以配置正弦波的数量,以及正弦波的频率和相位。这个示例同时展示了两种方法。
指定信号每个周期包含 50 个采样点,共 3 个周期。同时指定信号振幅范围在 -1 到 1 之间。
Period = 50; NumPeriod = 3; Range = [-1 1];
指定信号的频率范围。对于正弦波叠加信号,您需以奈奎斯特频率的分数形式指定通带的下限和上限频率。在此示例中,使用 0 至奈奎斯特频率之间的整个频率范围。
Band = [0 1];
首先使用正弦波的默认特性生成信号。默认情况下,该软件使用 10 个正弦波来生成信号。该软件为每个正弦波分配一个随机相位,然后将这些相位改变 10 次,以获得最小的信号扩散。信号扩散是指信号在所有采样点上的最小值与最大值之间的差值。
[u,freq] = idinput([Period 1 NumPeriod],'sine',Band,Range);该软件将正弦波叠加信号输出至 u,并将各正弦波的频率输出至 freq。freq 中的值是基于采样时间为 1 个时间单位进行缩放的。假设采样时间为 0.01 小时。要获取实际频率(单位:弧度/小时),需将值除以采样时间。
Ts = 0.01; % Sample time in hours
freq = freq/Ts;
freq(1)ans = 12.5664
freq(1) 是第一个正弦波的频率。要了解软件如何选择频率,请参阅 idinput 参考页面的 SineData 参量说明。
要验证信号是由 10 个正弦波生成的,可查看信号的频率成分。对信号进行傅里叶变换,并绘制信号的单边幅度谱。
ufft = fft(u); Fs = 2*pi/Ts; % Sampling frequency in rad/hour L = length(u); w = (0:L-1)*Fs/L; stem(w(1:L/2),abs(ufft(1:L/2))) % Plot until Nyquist frequency title('Single-Sided Amplitude Spectrum of u(t)') xlabel('Frequency (rad/hour)') ylabel('Amplitude')
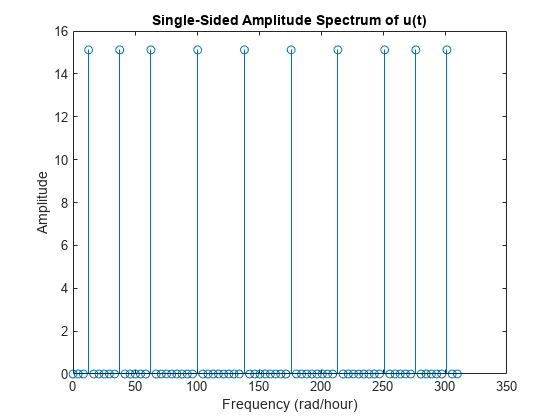
生成的图显示了用于生成信号的 10 个正弦波的频率分布。例如,该图显示第一个正弦波的频率为 12.57 弧度/小时,与 freq(1) 相同。
将生成的信号转换为 iddata 对象,并绘制该信号。将采样时间设定为 0.01 小时。
u = iddata([],u,Ts,'TimeUnit','hours'); plot(u)
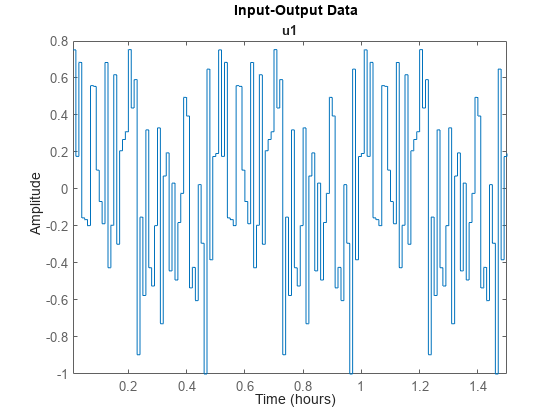
信号 u 由 10 个正弦波生成,周期为 0.5 小时,包含 3 个周期。
现在修改用于生成正弦波叠加信号的正弦波的数量、频率和相位。使用 12 个正弦波,并尝试 15 组不同的相位组合。要设置正弦波的频率,请指定 GridSkip = 2。该软件从频率网格 2*pi*[1:GridSkip:fix(Period/2)]/Period 与通带 pi*Band 的交点处选取正弦波的频率。
NumSinusoids = 12;
NumTrials = 15;
GridSkip = 2;
SineData = [NumSinusoids,NumTrials,GridSkip];
u2 = idinput([Period 1 NumPeriod],'sine',Band,Range,SineData);将生成的信号转换为 iddata 对象,并绘制该信号。
u2 = iddata([],u2,Ts,'TimeUnit','hours'); plot(u2)
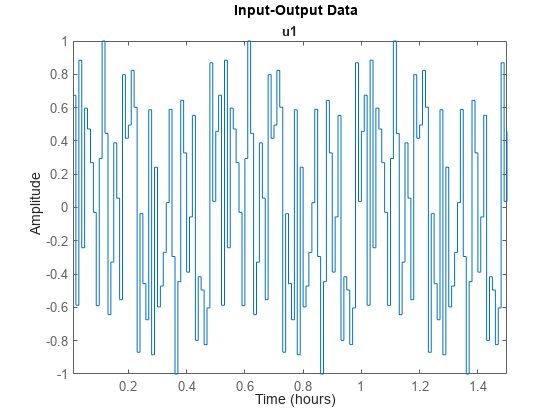
信号 u2 由 12 个正弦波生成,周期为 0.5 小时,包含 3 个周期。
输入参数
生成的信号中的输入通道数,指定为实数正整数。
每个周期内生成的信号样本数,指定为实数正整数。使用此输入来指定周期性信号。同时指定 NumPeriod 中的周期数。每个生成的输入通道信号包含 NumPeriod*Period 个采样点。
生成的信号周期数,指定为实数正整数。使用此输入来指定周期性信号。同时指定信号 Period。每个生成的输入通道信号包含 NumPeriod*Period 个采样点。
生成的信号类型,指定为以下值之一:
'rbs'- 生成随机二进制信号。随机二进制信号是一种仅取两个值的随机过程。您可以使用Range指定这些值。要生成带限信号,请在Band中指定通带。要生成周期信号,请指定Period和NumPeriod。'rgs'- 生成随机高斯信号。生成的正态信号具有均值 μ 和标准差 σ,使得 [μ-σ, μ+σ] 等于Range。要生成带限高斯信号,请在Band中指定通带。要生成具有n个采样点的周期高斯信号,该信号重复自身m次,请将Period设为n,并将NumPeriod设为m。'prbs'- 生成伪随机二进制信号 (PRBS)。伪随机本征信号 (PRBS) 是一种周期性、确定性的信号,具有类似白噪声的属性,其值在两个值之间交替变化。您可以使用Range指定这两个值。您还可以指定时钟周期,即信号值保持不变的最小采样间隔数。在Band中,您指定了时钟周期的倒数。生成的信号长度并不总是与您指定的长度相同。长度取决于您需要周期性信号还是非周期性信号,同时也取决于您指定的时钟周期。有关详细信息,请参阅伪随机二进制信号。
'sine'- 生成一个正弦波叠加信号。该软件将正弦波的频率均匀分布于选定的网格上,并为每个正弦波分配一个随机相位。该软件随后为每个正弦波尝试多个随机相位,并选择导致信号扩散最小的相位。信号扩散是指信号在所有采样点上的最小值与最大值之间的差值。生成的正弦波叠加信号的振幅经过缩放处理,以满足您指定的Range要求。您可以在
SineData参量中指定用于生成信号的正弦波特性,例如正弦波的数量及其频率间隔。
生成的信号频率范围,指定为包含最小和最大频率值的 1×2 行向量。
若
Type为'rgs'、'rbs'或'sine'- 则将Band指定为通带[wlow whigh]。其中,wlow和whigh分别表示通带的下限频率和上限频率,以奈奎斯特频率的分数形式表示。例如,要生成具有白噪声特性的输入,请使用Band = [0 1]。该软件使用
idfilt通过采用八阶巴特沃斯非因果滤波器,实现了随机高斯信号 ('rgs') 的频率成分。为生成随机二进制信号 ('rbs'),该软件采用相同的滤波器,随后将信号转换为二进制形式。因此,生成的随机二进制信号中的频率成分可能不符合指定的通带。对于
'sine'信号,正弦波的频率被选定为在指定通带内的选定网格上均匀分布。有关更多信息,请参阅SineData参量说明。若
Type等于'prbs'- 则将Band指定为[0 B],其中B是信号时钟周期的倒数。时钟周期是指信号值保持不变的最小采样间隔数。因此,生成的信号在长度为1/B个采样点的区间内保持恒定。如果1/B不是整数,则软件将使用floor(1/B)作为时钟周期。
生成的输入信号范围,指定为形式为 [umin,umax] 的两元素行向量。
若
Type为'rbs'或'prbs'- 则生成的信号u的值是umin或umax。若
Type为'sine'- 则生成的信号u的值介于umin与umax之间。若
Type为'rgs'- 生成的高斯信号具有均值 μ 和标准差 σ,使得umin和umax分别等于 μ-σ 和 μ+σ。例如,Range = [-1,1]返回一个均值为零、方差为一的加乌斯白噪声信号。
用于生成正弦波叠加信号的正弦波表征,以三元素行向量 [NumSinusoids,NumTrials,GridSkip] 形式定义。其中,
NumSinusoids是生成信号所使用的正弦波数量。默认值为10。NumTrials是指软件尝试寻找最小信号扩散时,正弦波中不同随机相对相位的数量。信号扩散是指信号在所有采样点上的最小值与最大值之间的差值。正弦波叠加信号的最大振幅取决于不同正弦波之间的相对相位。为寻找使信号扩散最小化的相位,软件尝试
NumTrials种不同的随机相位选择,以确定最佳相位值。例如,假设NumSinusoids是20,而NumTrials是5。该软件尝试了 20 个正弦波的 5 组不同相对相位,并选择能使信号扩散最小化的相位。NumTrials的默认值是10。GridSkip用于表征正弦波的频率。该软件从频率网格2*pi*[1:GridSkip:fix(Period/2)]/Period与通带pi*[Band(1) Band(2)]的交点处选取正弦波的频率。对于多通道输入信号,该软件会从该频率网格中选取不同的频率来生成不同的输入通道。您可以使用GridSkip来控制奇数和偶数频率倍频,例如用于检测不同类型的非线性现象。要提取软件选定用于生成信号的频率
freq,请使用以下语法。[u,freq] = idinput(__)
输出参量
详细信息
伪随机二进制信号 (PRBS) 是一种周期性、确定性的信号,具有类似白噪声的属性,其值在两个值之间交替变化。
以如下方式生成 PRBS:
此处, 表示历史输入向量,n 表示伪随机二进制序列 (PRBS) 阶数,rem 表示将 除以 2 后的余数。因此,伪随机比特序列只能取值 0 和 1。该软件会根据您指定的 Range 对这些值进行缩放。此外,过去输入的向量 只能取 2n 个值。在这些值中,所有元素均为零的状态将被忽略,因为它将导致未来信号等于零。因此,伪随机二进制序列本质上是一种周期信号,其最大周期长度为 2n-1。下表列出了不同 PRBS 序列中 n 的最大可能长度。
| 阶数 n | 最大长度 PRBS (2n-1) |
|---|---|
| 2 | 3 |
| 3 | 7 |
| 4 | 15 |
| 5 | 31 |
| 6 | 63 |
| 7 | 127 |
| ⋮ | ⋮ |
| 32 | 4294967295 |
注意
该软件不会生成周期大于 232-1 的信号。
由于伪随机二进制序列 (PRBS) 具有固有的周期性,生成的信号长度和周期取决于您指定的时钟周期,以及您需要周期性信号还是非周期性信号。时钟周期是指信号值保持不变的最小采样间隔数。您在 Band 中指定时钟周期。
时钟周期 = 1 个采样 (Band = [0 B] = [0 1]):
要生成长度为
N的 nonperiodic signal 序列(其中NumPeriod= 1),软件首先计算一个周期大于N的最大长度伪随机比特序列 (PRBS)。该软件随后将 PRBS 的前N个样本返回为u。此操作确保u不是周期性的。例如,若N为 100,软件将生成周期为 127(阶数为 7)的最大长度伪随机序列,并返回前 100 个采样点作为u。有关示例,请参阅生成非周期伪随机二进制输入信号。
为生成 periodic signal(
NumPeriod> 1),软件通过调整信号周期来获得具有最大长度 PRBS 的整数倍。为此,该软件计算出阶数为n = floor(log2(Period))、周期为P = 2n-1的伪随机二进制序列 (PRBS)。信号u随后被生成,其形式为周期为P的该伪随机二进制序列信号重复NumPeriod次。因此,u的长度为P*NumPeriod。有关示例,请参阅生成周期性伪随机二进制输入信号。
在多输入通道情况下,信号发生最大偏移。也就是说,不同输入之间的重叠被最小化。这意味着
Period/NumPeriod是使用此类信号可估计的建模阶数的上限。
时钟周期 > 1 个采样 (Band = [0 B], where B<1):
生成的信号必须保持恒定至少 1/B 个采样点。为满足此要求,软件首先计算出可能的最大长度伪随机比特序列 (PRBS) 的序列为 n = floor(log2(Period*B)),周期为 2n-1。该软件随后对伪随机二进制序列进行拉伸,使得拉伸后信号的周期为 P = B-1(2n-1)。
若要生成长度为
N的 nonperiodic signal,当拉伸信号的周期P大于或等于N时,软件将返回拉伸信号的前N个采样点作为u。这确保了u在每个1/B采样点上是非周期性的,但保持恒定。请注意,对于非周期信号,Period等于N。若周期
P小于N,则软件改为计算阶数为n2 = n+1的最大长度伪随机比特序列。该软件随后将此伪随机序列拉伸,使其周期变为P2 = B-1(2n2-1)。该软件随后将此信号的前N个采样点作为u返回。要生成 periodic signal,软件会将周期为
P的拉伸信号重复NumPeriod次,从而生成u。因此,u的长度为P*NumPeriod。
有关示例,请参阅生成具有指定时钟周期的伪随机二进制输入信号。
参考
[1] Söderström, T. and P. Stoica., Chapter C5.3 in System Identification, Prentice Hall, 1989.
[2] Ljung, L., Section 13.3 in System Identification: Theory for the User, Prentice Hall PTR, 1999.
版本历史记录
在 R2006a 之前推出
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)