Main Content

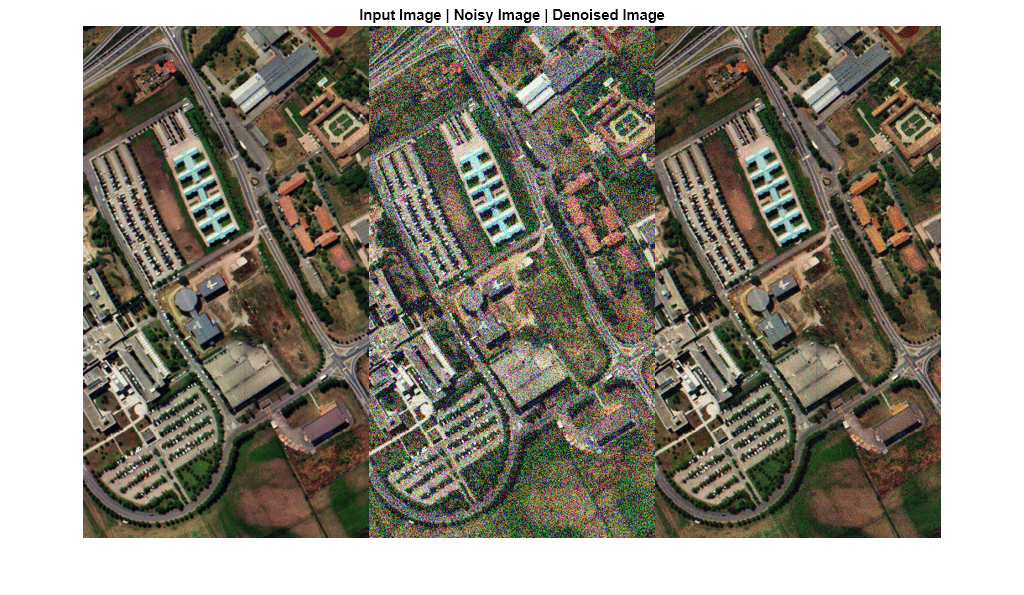
denoiseNGMeet

Denoise hyperspectral images using non-local meets global approach

Since R2020b

collapse all in page

Syntax

outputData = denoiseNGMeet(inputData)
outputData = denoiseNGMeet(inputData,Name,Value)

Description

outputData = denoiseNGMeet(inputData) reduces noise in hyperspectral data by using the non-local meets global (NGMeet) approach. This is an iterative approach that integrates both the spatial non-local similarity and spectral low-rank approximation for estimating the original pixel values. For more information, see Algorithms.

example

outputData = denoiseNGMeet(inputData,Name,Value) specifies options using one or more name-value arguments. Use this syntax to set the parameter values for the NGMeet approach.

Note

This function requires the Hyperspectral Imaging Library for Image Processing Toolbox™. You can install the Hyperspectral Imaging Library for Image Processing Toolbox from Add-On Explorer. For more information about installing add-ons, see Get and Manage Add-Ons.

The Hyperspectral Imaging Library for Image Processing Toolbox requires desktop MATLAB®, as MATLAB Online™ or MATLAB Mobile™ do not support the library.

example

Examples

collapse all

This example uses:

Open Live Script

Read hyperspectral data into the workspace.

hcube = hypercube('paviaU.hdr');

Normalize the input data and add Gaussian noise to the normalized input data.

hcube = hypercube(rescale(hcube.DataCube),hcube.Wavelength);
inputData = imnoise(hcube.DataCube,'Gaussian',0,0.005);
inputData = assignData(hcube,':',':',':',inputData);

Denoise the noisy hyperspectral data using NGmeet method.

outputData = denoiseNGMeet(inputData);

Estimate RGB images for the input, noisy, and the denoised output datacube. Increase the image contrast by applying contrast stretching.

originalImg = colorize(hcube,'Method','rgb','ContrastStretching',true);
noisyImg = colorize(inputData,'Method','rgb','ContrastStretching',true);
denoisedImg = colorize(outputData,'Method','rgb','ContrastStretching',true);

Display RGB images of the original, noisy, and denoised data.

figure
montage({originalImg,noisyImg,denoisedImg})
title('Input Image | Noisy Image | Denoised Image');

Figure contains an axes object. The hidden axes object with title Input Image | Noisy Image | Denoised Image contains an object of type image.

This example uses:

Open Live Script

Read hyperspectral data into the workspace.

hcube = hypercube('paviaU.hdr');

Normalize the input data and add Gaussian noise to the normalized input data.

hcube = hypercube(rescale(hcube.DataCube),hcube.Wavelength);
inputData = imnoise(hcube.DataCube,'Gaussian',0,0.005);
inputData = assignData(hcube,':',':',':',inputData);

Denoise the noisy hyperspectral data by using the NGmeet method. Set the smoothing parameter value to 0.01 and the number of iterations to 4.

outputData = denoiseNGMeet(inputData,'Sigma',0.01,'NumIterations',2);

Estimate RGB images for the input, noisy, and the denoised output datacube. Increase the image contrast by applying contrast stretching.

originalImg = colorize(hcube,'Method','rgb','ContrastStretching',true);
noisyImg = colorize(inputData,'Method','rgb','ContrastStretching',true);
denoisedImg = colorize(outputData,'Method','rgb','ContrastStretching',true);

Display RGB images of the original, noisy, and denoised data.

figure
montage({originalImg,noisyImg,denoisedImg})
title('Input Image | Noisy Image | Denoised Image');

Figure contains an axes object. The hidden axes object with title Input Image | Noisy Image | Denoised Image contains an object of type image.

Input Arguments

collapse all

Input hyperspectral data, specified as a 3-D numeric array that represent the hyperspectral data cube of size M-by-N-by-C or hypercube object. If the input is a hypercube object, the function reads the data cube stored in the DataCube property of the object. The hyperspectral data cube must be real and non-sparse. If the size of the hyperspectral data cube is M-by-N-by-C, both M and N must be greater than 16.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: denoiseNGMeet(hcube,"Sigma",0.3)

Smoothing parameter, specified as a positive scalar. The default value is 0.1 times the noise variance (σn). Increasing this value increases the level of smoothing in the denoised output.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Number of spectral bands in low-rank approximation, specified as a positive integer in the range (0, C]. C is the number of bands in the input data. The number of endmembers in the hyperspectral data can be a good estimate for the number of spectral bands to use for low-rank approximation. You can find the number of endmembers in the input hyperspectral data by using the countEndmembersHFC function. The values of the name-value arguments SpectralSubspace and NumIterations must satisfy the condition SpectralSubspace + 2*(NumIterations - 1) <= C.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Number of iterations, specified as a positive integer. Increase this value for better denoising results. The values of the name-value arguments SpectralSubspace and NumIterations must satisfy the condition SpectralSubspace + 2*(NumIterations - 1) <= C.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Output Arguments

collapse all

Denoised hyperspectral data, returned as a 3-D numeric array or hypercube object.

Algorithms

The NGMeet method estimates the denoised data cube by using these steps. For each iteration, i

  1. Compute spectral low-rank approximation of the noisy input data (Yi) by using singular value decomposition. The approximation results in a reduced data cube (Mi) and the related orthogonal basis Ai.

  2. Perform spatial denoising of the reduced data cube Mi by using non-local similarity filtering. You can control the degree of smoothing by specifying the smoothing parameter 'Sigma'.

  3. Perform inverse projection. Map the denoised reduced data cube Mi to original space by using the orthogonal basis Ai. The result is the denoised output (Xi) obtained at iteration i.

  4. Perform iterative regularization. Update the noisy input data, Yi+1 = λXi + (1-λ)Yi.

  5. Repeat steps 1 to 4, for the specified number of iterations. The final value Xi is the denoised hyperspectral data.

References

[1] He, Wei, Quanming Yao, Chao Li, Naoto Yokoya, and Qibin Zhao. “Non-Local Meets Global: An Integrated Paradigm for Hyperspectral Denoising.” In 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 6861–70. Long Beach, CA, USA: IEEE, 2019. https://doi.org/10.1109/CVPR.2019.00703.

Version History

Introduced in R2020b

expand all

See Also

|