Main Content

obliqueslice

Extract oblique slice from 3-D volumetric data

Since R2020a

collapse all in page

Syntax

B = obliqueslice(V,point,normal)
B = obliqueslice(V,point,normal,Name=Value)
[B,x,y,z] = obliqueslice(___)

Description

B = obliqueslice(V,point,normal) extracts a 2-D oblique slice from a 3-D volumetric data V. The slice is extracted with reference to a given point on the volume and a normal vector. The slicing plane is perpendicular to the normal vector and passes through the specified point.

For information about how the slice is extracted with respect to the given point and the normal, see Oblique Slicing.

example

B = obliqueslice(V,point,normal,Name=Value) specifies options using one or more name-value arguments.

example

[B,x,y,z] = obliqueslice(___) also returns the 3-D Cartesian coordinates of the extracted slice in the input volume. For information about how the intensity values at these 3-D coordinates are mapped to 2-D plane, see Mapping Values from 3-D Coordinate Space to Image Plane.

example

Examples

collapse all

Open Live Script

Load a 3-D volumetric data set into the workspace. 

load mri

Remove singleton dimensions by using the squeeze function.

V = squeeze(D);

Display horizontal slices of the data by using the montage function.

montage(V,map,'Size',[3 9]);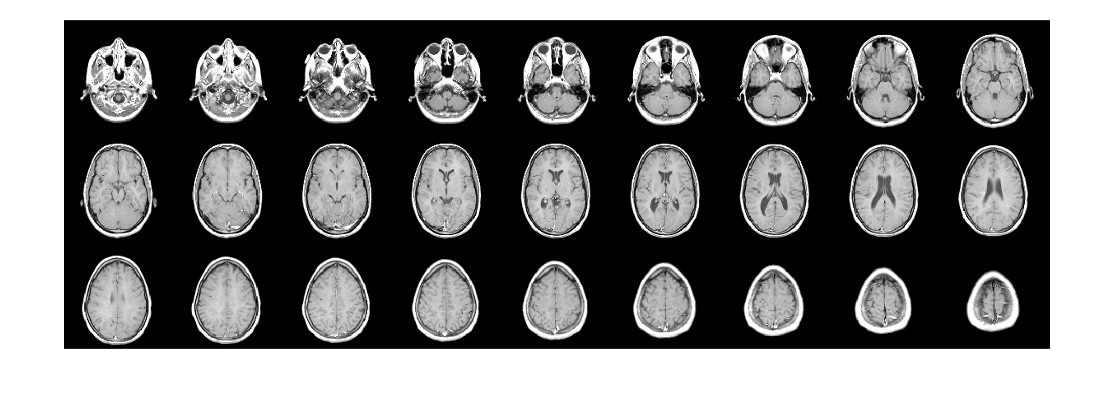

Figure contains an axes object. The hidden axes object contains an object of type image.

Specify a point in the volume for the slice to pass through. 

point = [73 50 15.5];

Specify a normal vector in 3-D coordinate space.

normal = [0 15 20];

Extract a slice from the volumetric data. The slice is perpendicular to the normal vector and passes through the specified point.

[B,x,y,z] = obliqueslice(V,point,normal);

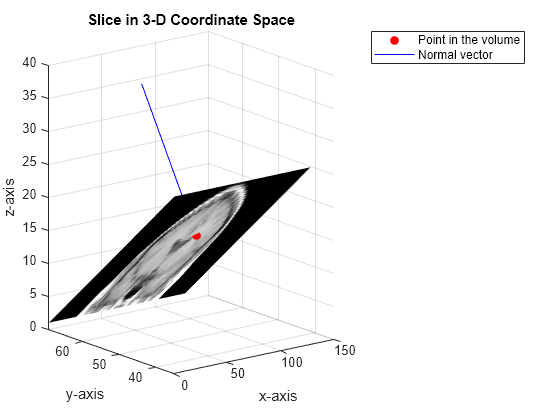
Display the extracted slice in the 3-D coordinate space.

figure
surf(x,y,z,B,'EdgeColor','None','HandleVisibility','off');
grid on
view([-38 12])
colormap(gray)
xlabel('x-axis')
ylabel('y-axis');
zlabel('z-axis');
title('Slice in 3-D Coordinate Space')

Plot the point and the normal vector.

hold on
plot3(point(1),point(2),point(3),'or','MarkerFaceColor','r');
plot3(point(1)+[0 normal(1)],point(2)+[0 normal(2)],point(3)+[0 normal(3)], ...
    '-b','MarkerFaceColor','b');
hold off
legend('Point in the volume','Normal vector')

Figure contains an axes object. The axes object with title Slice in 3-D Coordinate Space, xlabel x-axis, ylabel y-axis contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Point in the volume, Normal vector.

Display the extracted slice in the image plane.

figure
imshow(B,[])
title('Slice in Image Plane')

Figure contains an axes object. The hidden axes object with title Slice in Image Plane contains an object of type image.

Open Live Script

Load a 3-D volumetric data set into the workspace.

s = load(fullfile(toolboxdir('images'),'imdata','BrainMRILabeled','images','vol_001.mat'));
V = s.vol;

Display horizontal slices of the data by using the montage function.

montage(V,'Indices',12:118,'Size',[8 12],'DisplayRange',[]);

Figure contains an axes object. The hidden axes object contains an object of type image.

Specify the normal vector to a plane in 3-D coordinate space.

normal = [20 0 10];

Extract multiple slices along the direction of the normal vector using a for loop. In each iteration:

  • Specify a point that the slice has to pass through.

  • Extract the slice, specifying the output size to 'Full' and the fill value for padding pixels as 255. The extracted slices are perpendicular to the normal vector and pass through the specified point.

  • Display the extracted slices. 

sliceIdx = 10:5:180;

figure
for s = 1:length(sliceIdx)
    
    pt = [sliceIdx(s) 150 80];
    [B,x,y,z] = obliqueslice(V,pt,normal,'OutputSize','Full','FillValues',255);

    Bslices(:,:,s) = B;

    % Display the slice in 3-D coordinate space
    subplot('Position',[0.11 0.36 0.38 0.5])
    surf(x,y,z,B,'EdgeColor','None','HandleVisibility','off');
    grid on
    view([-24 12])
    colormap(gray)
    xlabel('x-axis')
    ylabel('y-axis');
    zlabel('z-axis');
    zlim([0 155]);
    ylim([0 250]);
    xlim([0 250]);
    title('Slice in 3-D Coordinate Space') 
    % Plot the point and the normal vector.
    hold on
    plot3(pt(1),pt(2),pt(3),'or','MarkerFaceColor','r')
    plot3( ...
        pt(1)+[-normal(1) normal(1)], ...
        pt(2)+[-normal(2) normal(2)], ...
        pt(3)+[-normal(3) normal(3)], ...
        '-b','MarkerFaceColor','b')
    legend('Point in the volume','Normal vector','Position',[0.1 0.12 0.3 0.08])
    hold off   
    % Display the extracted slice.
    subplot('Position',[0.6 0.37 0.34 0.49])
    imshow(B,[])
    title('Slice in Image Plane')
    pause(0.5);  
end

Figure contains 2 axes objects. Axes object 1 with title Slice in 3-D Coordinate Space, xlabel x-axis, ylabel y-axis contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Point in the volume, Normal vector. Hidden axes object 2 with title Slice in Image Plane contains an object of type image.

Display the extracted image slices by using the montage function.

figure
montage(Bslices,'Size',[5 7],'DisplayRange',[]);

Figure contains an axes object. The hidden axes object contains an object of type image.

Input Arguments

collapse all

Input volume, specified as a 3-D numeric array or 3-D categorical array.

Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical | categorical

Point in the volume, specified as a 3-element row vector of the form [px py pz].

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Normal vector, specified as a 3-element row vector of form [a b c]. The normal vector is a vector that is perpendicular to a surface or plane.

To extract an orthogonal slice, you can set the normal vector to one of these values:

  • [1 0 0] — Extract slice in the yz-plane.

  • [0 1 0] — Extract slice in the xz-plane.

  • [0 0 1] — Extract slice in the xy-plane.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: obliqueslice(V,point,normal,OutputSize="Full")

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: obliqueslice(V,point,normal,"OutputSize","Full")

Interpolation method, specified as one of these values:

  • "linear" — linear interpolation

  • "nearest" — nearest neighbor interpolation

If V is numeric, the interpolation method defaults to "linear" but can also be specified as "nearest". If V is categorical, then the interpolation method must be "nearest".

Data Types: char | string

Size of output image, specified as one of these values:

  • "limit" — The size of the output image is the actual size of the 2-D slice with respect to the dimensions of input volume. If the extracted slice region is not square or rectangular, the function automatically pads the extracted slice region with extra pixels to yield a square or rectangular image.

  • "full" — The size of the output image may not be equal to the actual size of the 2-D slice. The size of the output image is set to the maximal slice size that can be obtained from the input volume with respect to the normal vector normal. To resize the image, the border of the extracted 2-D slice is padded with extra rows and columns.

    The fill value for the padded pixels is 0 by default. You can use the FillValues name-value argument to change the value.

Data Types: char | string

Fill value for padded pixels, specified as a numeric scalar, character vector, or missing.

When V is a numeric array, specify

  • 0 for zero padding.

  • a numeric scalar for constant padding.

When V is a categorical array, specify

  • a character vector that denotes a category in the input data. To know the categories, use the categories function.

  • missing, if the category in input data is equal to <undefined>.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | char

Output Arguments

collapse all

Output 2-D slice, returned as a numeric or categorical matrix. The data type of the output slice is same as the data type of the input volume.

Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical | categorical

x-coordinates of the output slice in the 3-D volume, returned as a numeric matrix of the size same as the output slice, B.

Data Types: single

y-coordinates of the output slice in the 3-D volume, returned as a numeric matrix of the size same as the output slice, B.

Data Types: single

z-coordinates of the output slice in the 3-D volume, returned as a numeric matrix of the size same as the output slice, B.

Data Types: single

More About

collapse all

Oblique Slicing

Given a point (px, py, pz) and the normal vector (a, b, c), the function solves the plane equation a(x-px)+b(y-py)+c(z-pz) = 0

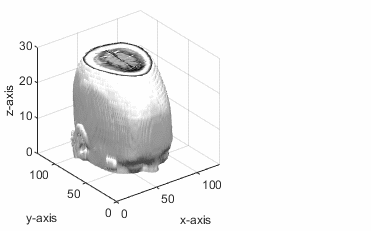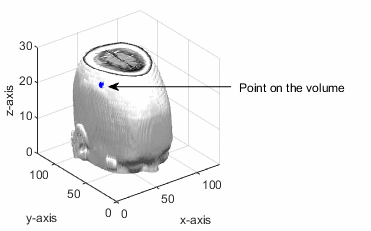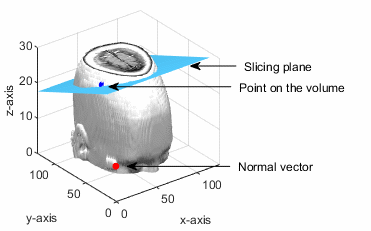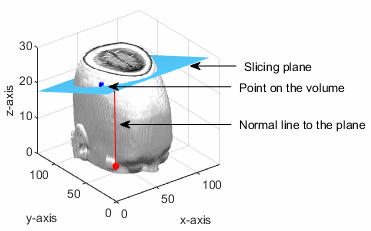
The point (px, py, pz) lies in the volumetric data. The slicing plane is perpendicular to the normal vector and passes through the given point.

Mapping Values from 3-D Coordinate Space to Image Plane

The order in which the coordinates of the extracted slice in 3-D space is mapped to a 2-D plane depends on its inclination angle with respect to the horizontal and vertical planes.

The obliqueslice function returns the output matrices x, y, and z that contain the x, y, z coordinates of the points in 3-D coordinate space that form the image slice. The obliqueslice function interpolates the intensity values at these points and maps it to the 2-D plane. The first value in the output matrices x(1,1), y(1,1), z(1,1) specify 3-D coordinate of a point that maps as the upper-left pixel, (1, 1) in the image plane. Starting from this point, the 3-D coordinates that constitute the image slice along with the associated intensity values are read in left-to-right, top-to-bottom scan order. These intensity values fill the 2-D image plane in the same left-to-right, top-to-bottom scan order.

Suppose V is the input volumetric data and B is the output 2-D image, then B(i,j) = V(a,b,c).

Where, a = x(i,j), b = y(i,j), and c = z(i,j).

Extended Capabilities

Version History

Introduced in R2020a

expand all

See Also

Functions

Objects