hgtransform 支持的变换

变换对象

变换对象的 Matrix 属性将变换同时应用到对象的所有子对象。变换包括旋转、转换和缩放。定义一个 4×4 变换矩阵的变换。

创建变换矩阵

makehgtform 函数简化了执行旋转、转换和缩放来构造矩阵的过程。有关创建使用 makehgtform 创建变换矩阵的详细信息，请参阅嵌套变换，执行复杂移动。

旋转

旋转变换遵守右手定则 - 将对象绕 x、y 或 z 轴旋转，以正角度按逆时针旋转，同时沿着各轴指向原点。如果旋转角度是 theta，以下矩阵定义了绕 x 轴旋转 theta。

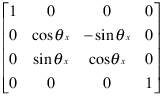
要定义任意轴旋转的变换矩阵，使用 makehgtform 函数。

转换

平移变换将对象相对于当前位置进行移动。转换可指定为采用数据空间单位的距离 t_x、t_y 和 t_z。以下矩阵显示变换矩阵中这些元素的位置。

缩放

缩放变换会改变对象的大小。指定缩放因子 s_x、s_y 和 s_z 并构造以下矩阵。

不能使用小于或等于零的缩放因子。

默认变换

默认变换是单位矩阵，您可以使用 eye 函数来创建它。以下是单位矩阵。

请参阅撤消变换操作。

不允许的变换：透视

透视变换会改变您观察对象的距离。以下矩阵为透视变换矩阵示例，这在 MATLAB^® 图形中是不允许的。

$[\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & p_{x} & 0 \end{matrix}]$

在本例中，p_x 是透视因子。

不允许的变换：剪切

剪切变换保持给定直线（或三维坐标中的平面）上所有点固定，同时将其他所有平行于直线（或平面）的点根据其与直线（或平面）的垂直距离成比例移动。以下矩阵为剪切变换矩阵示例，这在 hgtransform 中不允许。

$[\begin{matrix} 1 & s_{x} & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]$

在此例中，s_x 是剪切因子，可以替换单位矩阵中的任意零元素。

绝对变换与相对变换

变换以绝对形式指定，不相对于当前变换。例如，如果首先应用将变换对象在 x 方向上转换 5 个单位的变换，然后应用将变换对象在 y 方向上转换 4 个单位的变换，那么对象最后的位置在 y 方向上偏离原始位置 4 个单位。

如果您将变换进行累积，您必须将各个变换串联到一个矩阵中。请参阅将变换合并到一个矩阵。

将变换合并到一个矩阵

通过将单个矩阵串联（或相乘）并把 Matrix 属性设置为结果，来将各种变换合并到一个矩阵中，这样往往更加高效。矩阵乘法不适用交换律，因此矩阵相乘的顺序会影响结果。

例如，您想要先执行缩放，再转换，最后旋转。假设 R、T 和 S 是各个变换矩阵，按以下顺序相乘：

C = R*T*S % operations are performed from right to left

S 是缩放矩阵，T 是平移矩阵，R 是旋转矩阵，C 是三种操作的复合矩阵。然后将变换对象的 Matrix 属性设置为 C：

hg = hgtransform('Matrix',C);

将变换乘以单位矩阵

以下两组语句并不等价。第一组：

hg.Matrix = C;
hg.Matrix = eye(4);

结果是消除变换 C。第二组：

I = eye(4);
C = I*R*T*S;
hg.Matrix = C;

应用变换 C。将单位矩阵串联到其他矩阵对复合矩阵无效。

撤消变换操作

由于变换操作是以绝对形式指定（不相对于当前变换），您可以通过将当前变换设置为单位矩阵来撤消一系列变换。例如：

hg = hgtransform('Matrix',C);
...
hg.Matrix = eye(4);

将变换对象 hg 所包含的对象返回到其方向，然后再应用变换 C。

有关单位矩阵的详细信息，请参阅 eye 函数。

另请参阅

hgtransform | makehgtform | eye