球体内的随机数
此示例说明如何按照 Knuth [1] 所述的方法在球体内创建随机点。本例中的球体以原点为中心,半径为 3。
在球体内创建点的方法之一是在球面坐标中指定这些点。然后可以将其转换为笛卡尔坐标进行绘图。
首先,初始化随机数生成器,以使本示例中的结果具备可重复性。
rng(0,'twister')计算球体中各个点的仰角。这些值在开区间 内,但不是均匀分布的。
rvals = 2*rand(1000,1)-1; elevation = asin(rvals);
为球体中的各个点创建方位角。这些值在开区间 内均匀分布。
azimuth = 2*pi*rand(1000,1);
为球体中的各个点创建半径值。这些值在开区间 内,但不是均匀分布的。
radii = 3*(rand(1000,1).^(1/3));
转换为笛卡尔坐标并绘制结果。
[x,y,z] = sph2cart(azimuth,elevation,radii); figure plot3(x,y,z,'.') axis equal
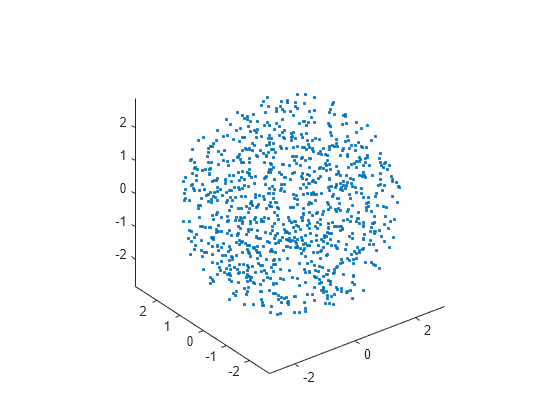
如果需要将随机数置于球体表面上,则指定一个常量半径值作为 sph2cart 的最后一个输入参量。在本例中,该值为 3。
[x,y,z] = sph2cart(azimuth,elevation,3);
参考
[1] Knuth, D. The Art of Computer Programming.Vol. 2, 3rd ed. Reading, MA:Addison-Wesley Longman, 1998, pp. 134–136.