求解具有多边界条件的 BVP

以下示例说明如何求解多点边界值问题，其中关注的解满足积分区间内的条件。

对于 $[0, λ]$ 中的 $x$ ，考虑以下方程

$v^{'} = \frac{C - 1}{n}$ ,

$C^{'} = \frac{vC - \min (x, 1)}{η}$ .

问题的已知参数是 $n$ 、 $κ$ 、 $λ > 1$ 和 $η = \frac{λ^{2}}{n \cdot κ^{2}}$ 。

$C^{'} (x)$ 的方程中的项 $\min (x, 1)$ 在 $x = 1$ 处不平滑，因此该问题不能直接求解。在这种情况下，您可以将问题分成两部分：一部分在区间 $[0, 1]$ 内，另一部分在区间 $[1, λ]$ 内。这两个区域之间的联系是在 $x = 1$ 处的解必须为连续的。解还必须满足边界条件

$v (0) = 0$ ,

$C (λ) = 1$ .

每个区域的方程如下

区域 1： $0 \leq x \leq 1$

$v^{'} = \frac{C - 1}{n}$ ,

$C^{'} = \frac{vC - x}{η}$ .

区域 2： $1 \leq x \leq λ$

$v^{'} = \frac{C - 1}{n}$ ,

$C^{'} = \frac{vC - 1}{η}$ .

交界点 $x = 1$ 同时包含在这两个区域中。在此交界点上，求解器会产生左解和右解，这两个解必须相等，以确保解的连续性。

要在 MATLAB® 中对此方程组求解，您需要先编写方程组、边界条件和初始估计值的代码，然后再调用边界值问题求解器 bvp5c。您可以将所需的函数作为局部函数包含在文件末尾（如本处所示），或者将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。

编写方程代码

$v^{'} (x)$ 和 $C^{'} (x)$ 的方程取决于正在求解的区域。对于多点边界值问题，导数函数必须接受第三个输入参数 region，该参数用于标识正在计算导数的区域。求解器从左到右对区域进行编号，从 1 开始。

创建一个函数以使用签名 dydx = f(x,y,region,p) 来编写方程代码，其中：

x 是自变量。
y 是因变量。
dydx(1) 给出 $v^{'} (x)$ 的方程，dydx(2) 给出 $C^{'} (x)$ 的方程。
region 是计算导数的区域编号（本例中问题分为两个区域，region 为 1 或 2）。
p 是向量，包含常量参数 $[n, κ, λ, η]$ 的值。

根据要求解的具体区域，使用 switch 语句返回不同方程。函数是

function dydx = f(x,y,region,p) % equations being solved
n = p(1);
eta = p(4);

dydx = zeros(2,1);
dydx(1) = (y(2) - 1)/n;

switch region
    case 1    % x in [0 1]
        dydx(2) = (y(1)*y(2) - x)/eta;
    case 2    % x in [1 lambda]
        dydx(2) = (y(1)*y(2) - 1)/eta;
end
end

注意：所有函数都作为局部函数包含在示例的末尾。

编写边界条件代码

在两个区域中求解两个一阶微分方程需要四个边界条件。这些条件中有两个来自原始问题：

$v (0) = 0$ ,

$C (λ) - 1 = 0$ .

另外两个条件强制交界点 $x = 1$ 处的左解和右解具备连续性：

$v_{L} (1) - v_{R} (1) = 0$ ,

$C_{L} (1) - C_{R} (1) = 0$ .

对于多点 BVP，边界条件函数 YL 和 YR 的参数会是矩阵。具体来说，第 k 列 YL(:,k) 是第 k 个区域左边界的解。YR(:,k) 则是第 k 个区域右边界的解。

在此问题中， $y (0)$ 通过 YL(:,1) 来逼近，而 $y (λ)$ 通过 YR(:,end) 来逼近。解在 $x = 1$ 处的连续性要求 YR(:,1) = YL(:,2)。

用于编写四个边界条件的残差值计算代码的函数是

function res = bc(YL,YR)
res = [YL(1,1)               % v(0) = 0
       YR(1,1) - YL(1,2)     % Continuity of v(x) at x=1
       YR(2,1) - YL(2,2)     % Continuity of C(x) at x=1
       YR(2,end) - 1];       % C(lambda) = 1
end

获取初始估计值

对于多点 BVP，边界条件自动应用于积分区间的开始处和结束处。但是，您必须在 xmesh 中为其他交界点分别指定双重项。满足边界条件的简单估计值是常量估计值 y = [1; 1]。

xc = 1;
xmesh = [0 0.25 0.5 0.75 xc xc 1.25 1.5 1.75 2];
yinit = [1; 1];
sol = bvpinit(xmesh,yinit);

求解方程

定义常量参数的值，并将其放入向量 p 中。使用语法 @(x,y,r) f(x,y,r,p) 向 bvp5c 提供函数，以提供参数向量。

计算 $κ$ 的几个值的解，其中使用每个解作为下一个解的初始估计值。对于 $κ$ 的每个值，计算渗透性 $Os = \frac{1}{v (λ)}$ 的值。对于循环的每次迭代，将计算值与近似解析解进行比较。

lambda = 2;
n = 5e-2;
for kappa = 2:5
   eta = lambda^2/(n*kappa^2);
   p = [n kappa lambda eta];
   sol = bvp5c(@(x,y,r) f(x,y,r,p), @bc, sol);
   K2 = lambda*sinh(kappa/lambda)/(kappa*cosh(kappa));
   approx = 1/(1 - K2);
   computed = 1/sol.y(1,end);
   fprintf('  %2i    %10.3f     %10.3f \n',kappa,computed,approx);
end

   2         1.462          1.454 
   3         1.172          1.164 
   4         1.078          1.071 
   5         1.039          1.034

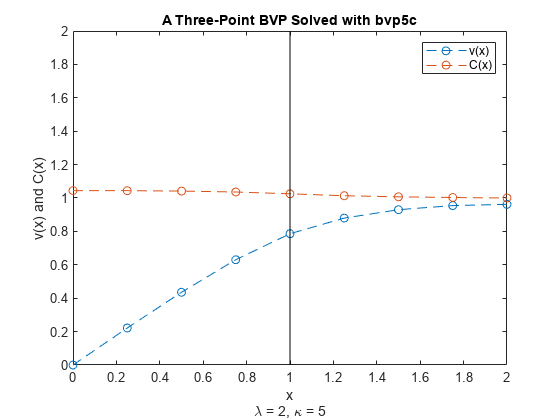
对解进行绘图

绘制 $v (x)$ 和 $C (x)$ 的解分量，以及在交界点 $x = 1$ 处的垂直线。显示的 $κ = 5$ 的解是循环的最后一次迭代的结果。

plot(sol.x,sol.y(1,:),'--o',sol.x,sol.y(2,:),'--o')
line([1 1], [0 2], 'Color', 'k')
legend('v(x)','C(x)')
title('A Three-Point BVP Solved with bvp5c')
xlabel({'x', '\lambda = 2, \kappa = 5'})
ylabel('v(x) and C(x)')

Figure contains an axes object. The axes object with title A Three-Point BVP Solved with bvp5c, xlabel x lambda blank = blank 2, blank kappa blank = blank 5, ylabel v(x) and C(x) contains 3 objects of type line. These objects represent v(x), C(x).

局部函数

此处列出了 BVP 求解器 bvp5c 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。

function dydx = f(x,y,region,p) % equations being solved
n = p(1);
eta = p(4);

dydx = zeros(2,1);
dydx(1) = (y(2) - 1)/n;

switch region
    case 1    % x in [0 1]
        dydx(2) = (y(1)*y(2) - x)/eta;
    case 2    % x in [1 lambda]
        dydx(2) = (y(1)*y(2) - 1)/eta;
end
end
%-------------------------------------------
function res = bc(YL,YR) % boundary conditions
res = [YL(1,1)               % v(0) = 0
       YR(1,1) - YL(1,2)     % Continuity of v(x) at x=1
       YR(2,1) - YL(2,2)     % Continuity of C(x) at x=1
       YR(2,end) - 1];       % C(lambda) = 1
end
%-------------------------------------------

另请参阅

bvp4c | bvp5c | bvpinit

求解具有多边界条件的 BVP

编写方程代码

编写边界条件代码

获取初始估计值

求解方程

对解进行绘图

局部函数

另请参阅

相关主题

WeChat