bvpinit

得出边界值问题求解器的初始估计值

语法

solinit = bvpinit(x,yinit)

solinit = bvpinit(sol,[anew bnew])

solinit = bvpinit(___,parameters)

说明

solinit = bvpinit(x,yinit) 使用初始网格 x 和初始解估计值 yinit 来得出边界值问题解的初始估计值。然后，您可以使用初始估计值 solinit 作为 bvp4c 或 bvp5c 的输入之一来求解边界值问题。

示例

solinit = bvpinit(sol,[anew bnew]) 得出区间 [anew bnew] 上解的初始估计值，其中 sol 是从 bvp4c 或 bvp5c 获得的解结构体。新区间 [anew bnew] 必须大于在其上定义 sol 的以前的区间。之前的解 sol 被外插到新区间。

solinit = bvpinit(___,parameters) 为边界值问题中具有未知值的参数指定初始估计值向量。您可以将此语法用于上述任一输入参量组合。

示例

全部折叠

BVP 解的初始估计值

打开实时脚本

创建 BVP 的解的初始估计值，用 bvp4c 求解 BVP，然后将解扩展到新域。

得出 BVP 问题的解的良好初始估计值可能是求解问题最困难的部分。BVP 解不一定唯一，因此初始估计值可以是求解器确定要返回的解的决定因素。初始估计值应该满足边界条件，其间的行为应该反映您对此问题的一般期望（解是否振荡，是否为简单的线性函数等）。

假设有以下微分方程：

${y^{'}}^{'} = - y$ .

该方程受限于边界条件

$y (0) = y (π) = 0$ .

将方程编码为一阶方程组的函数是

function dydx = bvpfun(x,y)
dydx = [y(2)
       -y(1)];
end

同样，对边界条件进行编码的函数是

function res = bcfun(ya,yb)
res = [ya(1)
       yb(1)];
end

您可以将所需的函数作为局部函数包含在文件末尾（如本处所示），也可以将它们作为单独的命名文件保存在 MATLAB® 路径上的目录中。

通过函数句柄提供初始估计值

您可以合理地预期方程的解是振荡的，因此使用正弦和余弦函数可以很好地得出解及其固定边界点之间导数的初始估计值。

function y = guess(x)
y = [sin(x)
     cos(x)];
end

使用域 $[0, π]$ 中的 10 个等距网格点和初始估计值函数创建一个解结构体。

xmesh = linspace(0,pi,10);
solinit = bvpinit(xmesh,@guess);

求解 BVP

使用 ode 函数、边界条件和解估计值调用 bvp4c。绘制结果。

sol = bvp4c(@bvpfun, @bcfun, solinit);
plot(sol.x,sol.y,'-o')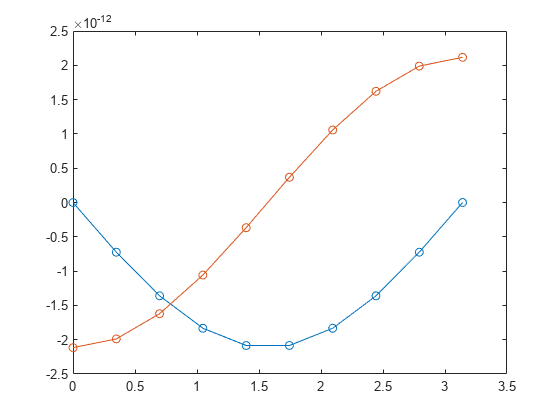

局部函数

此处列出了 BVP 求解器 bvp4c 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。

function dydx = bvpfun(x,y) % equation being solved
dydx = [y(2)
       -y(1)];
end
%-------------------------------------------
function res = bcfun(ya,yb) % boundary conditions
res = [ya(1)
       yb(1)];
end
%-------------------------------------------
function y = guess(x) % guess at solution behavior
y = [sin(x)
     cos(x)];
end
%-------------------------------------------

用外插法扩展 BVP 解

打开实时脚本

在初始区间上求解 BVP，然后使用每个解作为下一区间的初始估计值来迭代扩展区间。

假设使用以下方程

${y^{'}}^{'} = y$ .

如果要表示为一阶方程组，则包含以下两个方程：

${y_{1}}^{'} = y_{2}$ ,

${y_{2}}^{'} = y_{1}$ .

该方程最初在区间 $[0, 3]$ 上定义，并受限于边界条件

$y (0) = 0$ ,

$y (3) = 1$ .

将方程编码为一阶方程组的函数是

function dydx = bvpfun(x,y)
dydx = [y(2)
        y(1)];
end

同样，对边界条件进行编码的函数是

function res = bcfun(ya,yb)
res = [ya(1)
       yb(1)-1];
end

您可以将所需的函数作为局部函数包含在文件末尾（如本处所示），也可以将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。

初始估计值

使用指数函数作为解的初始估计值。由于方程有两个解分量，因此需要编写一个 y = guess(x) 形式的初始估计值函数，该函数返回向量。

function y = guess(x)
y = [exp(x)
     exp(x)];
end

包含五个点的网格足以捕获估计值函数的行为。

xmesh = linspace(0,3,5);
solinit = bvpinit(xmesh,@guess);

求解方程

在初始区间 $[0, 3]$ 中求解方程，并绘制 $y_{1}$ 的结果。

sol = bvp4c(@bvpfun, @bcfun, solinit);
plot(sol.x(1,:),sol.y(1,:),'-o')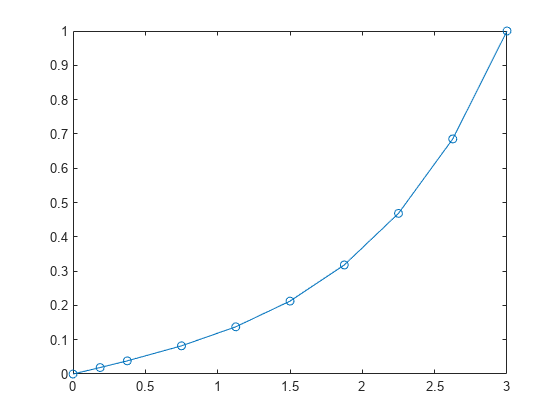

扩展区间

现在，使用 bvpinit 来循环扩展积分区间，求解每个新问题并绘图。在每次迭代中，使用外插至新区间 [0 k] 的上一个解 sol 得出初始估计值。在每个新问题中，bvp4c 会在新边界 [0 k] 上强制应用边界条件。

hold on
for k = 4:8
    solinit = bvpinit(sol,[0 k]);
    sol = bvp4c(@bvpfun, @bcfun, solinit);
    plot(sol.x(1,:),sol.y(1,:),'-o')
end

此示例显示了连续法的一个简化版本，这是一种很有用的方法，它通过将问题分解成更小的区间或更简单的问题来求解 BVP。有关此方法的更多示例，请参阅：

局部函数

此处列出了 BVP 求解器 bvp4c 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。

function dydx = bvpfun(x,y) % equation being solved
dydx = [y(2)
        y(1)];
end
%-------------------------------------------
function res = bcfun(ya,yb) % boundary conditions
res = [ya(1)
       yb(1)-1];
end
%-------------------------------------------
function y = guess(x) % guess at solution behavior
y = [exp(x)
     exp(x)];
end
%-------------------------------------------

输入参数

全部折叠

`x` — 初始网格
向量

初始网格，指定为向量。要在区间 [a,b] 上求解问题，请将 x(1) 指定为 a 并将 x(end) 指定为 b。x 的项必须为升序（如果 a < b）或降序（如果 a > b）。求解器会根据解调整此网格（通过添加、删除和移动网格点），因此诸如 x = linspace(a,b,10) 之类的估计值通常足以满足需求。为了处理比较难的问题，请在解快速变化的位置放置一些网格点。

对于两点边界值问题，x 的项必须唯一。即，如果 a < b，项必须满足 x(1) < x(2) < ... < x(end)。如果 a > b，项必须满足 x(1) > x(2) > ... > x(end)。
对于多点边界值问题，通过重复 x 中的项，可以在端点 a 和 b 之外，在 [a,b] 中指定应用边界条件的点。例如，假设有以下向量
```
x = [0 0.5 1 1 1.5 2];
```
对于此网格，在以下三个点应用边界条件：端点 0 和 2，以及重复项 1。一般说来，重复项表示 [a,b] 中区域之间的边界点。重复项 1 将区间 [0 2] 分为两个区域：[0 1] 和 [1 2]。

示例: solinit = bvpinit(linspace(a,b,10),yinit)

`yinit` — 解的初始估计值
向量 | 函数

解的初始估计值，指定为向量或函数。

向量 - 对于解的每个分量，bvpinit 在所有网格点上复制向量的对应元素作为常量估计值。也即，yinit(i) 是 x 中所有网格点处解的第 i 个分量 yinit(i,:) 的常量估计值。
函数 - 对于给定网格点而言，估计值函数必须返回一个向量，该向量的元素是解的对应分量的估计值。此函数必须采用以下格式
```
y = guess(x)
```
x 是网格点，y 是其长度与解中的分量数相同的向量。例如，如果 yinit 是函数，则在每个网格点上，bvpinit 都会调用
```
y(:,j) = guess(x(j))
```
对于多点边界值问题，估计值函数必须采用以下格式
```
y = guess(x,k)
```
y 是区域 k 中 x 处的解的初始估计值。该函数必须接受输入参量 k，提供此输入参量的目的是为了灵活编写估计值函数。但是，该函数不必使用 k。

示例: solinit = bvpinit(x,[sqrt(3)/2; 0])

示例: solinit = bvpinit(x,@guess)

`parameters` — 未知参数值的初始估计值
标量 | 向量

未知参数值的初始估计值，指定为标量或向量。

示例: solinit = bvpinit(x, yinit, [0 1 sqrt(2)]) 指定三个未知参数的估计值向量。

示例: 键入 edit mat4bvp 可查看具有一个未知参数的 BVP 的示例。

`sol` — 先前的解
结构体

先前的解，指定为由 bvp4c 或 bvp5c 返回的解结构体。如果 sol 包含参数，这些参数将被复制到 solinit。

数据类型: struct

输出参量

全部折叠

`solinit` — 解的初始估计值
结构体

解的初始估计值，以结构体形式返回。使用此结构体作为 bvp4c 或 bvp5c 的第三个输入来求解边界值问题。

扩展功能

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

版本历史记录

在 R2006a 之前推出

另请参阅

bvpinit

语法

说明

示例

BVP 解的初始估计值

用外插法扩展 BVP 解

输入参数

x — 初始网格 向量

yinit — 解的初始估计值 向量 | 函数

parameters — 未知参数值的初始估计值 标量 | 向量

sol — 先前的解 结构体

输出参量

solinit — 解的初始估计值 结构体

扩展功能

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

版本历史记录

另请参阅

WeChat

`x` — 初始网格
向量

`yinit` — 解的初始估计值
向量 | 函数

`parameters` — 未知参数值的初始估计值
标量 | 向量

`sol` — 先前的解
结构体

`solinit` — 解的初始估计值
结构体

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。