使用延拓验证 BVP 一致性

以下示例说明如何使用延拓将 BVP 的一个解逐渐扩展到更大的区间。

福克纳-斯坎边界值问题 [1] 源于为平板粘性不可压缩层流问题求取相似解的过程。示例方程是

${f^{'}}^{'}^{'} + f {f^{'}}^{'} + β (1 - {f^{'}}^{2}) = 0$ .

此问题位于无限区间 $[0, \infty]$ 和 $β = 0.5$ 上，并且需要满足边界条件

$f (0) = 0$ ,

$f^{'} (0) = 0$ ,

$f^{'} (\infty) = 1$ .

在无限区间上无法求解 BVP，在非常大的有限区间上求解 BVP 也不切实际。在这种情况下，此示例转而求解位于较小区间 $[0, a]$ 上的一系列问题，从而验证解具有与 $a \to \infty$ 一致的行为。这种做法称为延拓，它是将一个问题分解成多个更简单的问题，将每个小问题所反馈的解作为下一个小问题的初始估计值。

要在 MATLAB® 中对此方程组求解，您需要先编写方程组、边界条件和选项的代码，然后再调用边界值问题求解器 bvp4c。您可以将所需的函数作为局部函数包含在文件末尾（如本处所示），或者将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。

编写方程代码

创建一个函数以编写方程代码。此函数应具有签名 dfdx = fsode(x,f)，其中：

x 是自变量。
f 是因变量。

您可以使用代换法 $f_{1} = f$ 、 $f_{2} = f^{'}$ 和 $f_{3} = {f^{'}}^{'}$ 将三阶方程重写为一阶方程组。方程变为

${f_{1}}^{'} = f_{2}$ ,

${f_{2}}^{'} = f_{3}$ ,

${f_{3}}^{'} = - f_{1} f_{3} - β (1 - f_{2}^{2})$ .

对应的函数是

function dfdeta = fsode(x,f)
b = 0.5;
dfdeta = [ f(2)
           f(3)
          -f(1)*f(3) - b*(1 - f(2)^2) ];
end

注意：所有函数都作为局部函数包含在示例的末尾。

编写边界条件代码

现在，编写一个函数，该函数返回在边界点处的边界条件的残差值。此函数应具有签名 res = fsbc(f0,finf)，其中：

f0 是在区间的开始处的边界条件的值。
finf 是在区间的结束处的边界条件的值。

要计算残差值，您需要将边界条件设置为 $g (x, y) = 0$ 形式。在此形式中，边界条件是

$f (0) = 0$ ,

$f^{'} (0) = 0$ ,

$f^{'} (\infty) - 1 = 0$ .

对应的函数是

function res = fsbc(f0,finf)
res = [f0(1)
       f0(2)
       finf(2) - 1];
end

创建初始估计值

最后，您必须提供解的初始估计值。具有五个点的粗网格以及满足边界条件的常量估计值便可在区间 $[0, 3]$ 上进行收敛。变量 infinity 表示积分区间的右侧极限。随着 infinity 的值在随后的迭代中从 3 增加到其最大值 6，每个先前迭代给出的解充当下一次迭代的初始估计值。

infinity = 3;
maxinfinity = 6;
solinit = bvpinit(linspace(0,infinity,5),[0 0 1]);

求解方程并绘制解

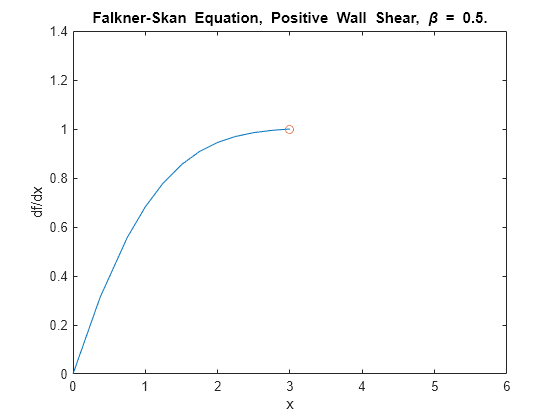
在初始区间 $[0, 3]$ 中求解问题。绘制解，并将 ${f^{'}}^{'} (0)$ 的值与解析值 [1] 进行比较。

sol = bvp4c(@fsode,@fsbc,solinit);
x = sol.x;
f = sol.y;
plot(x,f(2,:),x(end),f(2,end),'o');
axis([0 maxinfinity 0 1.4]);
title('Falkner-Skan Equation, Positive Wall Shear, \beta = 0.5.')
xlabel('x')
ylabel('df/dx')
hold on

Figure contains an axes object. The axes object with title Falkner-Skan blank Equation, blank Positive blank Wall blank Shear, blank beta blank = blank 0 . 5 ., xlabel x, ylabel df/dx contains 2 objects of type line. One or more of the lines displays its values using only markers

fprintf('Cebeci & Keller report that f''''(0) = 0.92768.\n')

Cebeci & Keller report that f''(0) = 0.92768.

fprintf('Value computed using infinity = %g is %7.5f.\n', ...
         infinity,f(3,1))

Value computed using infinity = 3 is 0.92915.

现在，通过为每次迭代增加 infinity 的值，在逐步增大的区间上求解问题。bvpinit 函数将每个解外推至新区间，以作为 infinity 的下一个值的初始估计值。每次迭代都会打印 ${f^{'}}^{'} (0)$ 的计算值，并将解的绘图叠加到之前的解上。当 infinity = 6 时，解的一致行为变得明显， ${f^{'}}^{'} (0)$ 的值非常接近预测值。

for Bnew = infinity+1:maxinfinity
  solinit = bvpinit(sol,[0 Bnew]); % Extend solution to new interval
  sol = bvp4c(@fsode,@fsbc,solinit);
  x = sol.x;
  f = sol.y;
  
  fprintf('Value computed using infinity = %g is %7.5f.\n', ...
           Bnew,f(3,1))
  plot(x,f(2,:),x(end),f(2,end),'o');
  drawnow
end

Value computed using infinity = 4 is 0.92774.
Value computed using infinity = 5 is 0.92770.
Value computed using infinity = 6 is 0.92770.

hold off

Figure contains an axes object. The axes object with title Falkner-Skan blank Equation, blank Positive blank Wall blank Shear, blank beta blank = blank 0 . 5 ., xlabel x, ylabel df/dx contains 8 objects of type line. One or more of the lines displays its values using only markers

局部函数

此处列出了 BVP 求解器 bvp4c 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。

function dfdeta = fsode(x,f) % equation being solved
dfdeta = [ f(2)
           f(3)
          -f(1)*f(3) - 0.5*(1 - f(2)^2) ];
end 
%-------------------------------------------
function res = fsbc(f0,finf) % boundary conditions
res = [f0(1)
       f0(2)
       finf(2) - 1];
end
%-------------------------------------------

参考

[1] Cebeci, T. and H. B. Keller."Shooting and Parallel Shooting Methods for Solving the Falkner-Skan Boundary-layer Equation."J. Comp.Phys., Vol. 7, 1971, pp. 289-300.

另请参阅

bvp4c | bvp5c | bvpinit