求解具有奇异项的 BVP
以下示例说明如何求解埃姆登方程,埃姆登方程是一个具有奇异项的边界值问题,源于对气体球体建模的过程。
在使用对称性法简化模型的 PDE 后,该方程变为在区间 上定义的二阶 ODE,
.
在 处, 项具有奇异性,但对称性表示边界条件 。通过此边界条件,项 可以很好地定义为 。对于边界条件 ,BVP 有解析解,可以将该解与 MATLAB® 中计算的数值解进行比较,
.
BVP 求解器 bvp4c 可以求解以下形式的奇异 BVP
.
矩阵 必须为常量, 处的边界条件必须与必要条件 一致。使用 bvpset 的 'SingularTerm' 选项将 S 矩阵传递给求解器。
您可以使用 和 将埃姆登方程重写为一阶方程组
,
.
边界条件变为
,
.
采用要求的矩阵形式,方程组表示为
.
采用矩阵形式时,很明显, 且 。
要在 MATLAB 中对此方程组求解,您需要先编写方程组、边界条件和选项的代码,然后再调用边界值问题求解器 bvp4c。您可以将所需的函数作为局部函数包含在文件末尾(如本处所示),或者将它们作为单独的命名文件保存在 MATLAB 路径上的目录中。
编写方程代码
创建一个函数以用于编写 的方程代码。此函数应具有签名 dydx = emdenode(x,y),其中:
x是自变量。y是因变量。dydx(1)给出 的方程,dydx(2)给出 的方程。
求解器会自动将这些输入传递给该函数,但是变量名称决定如何编写方程代码。在这种情况下:
function dydx = emdenode(x,y) dydx = [y(2) -y(1)^5]; end
包含 S 的项通过选项传递给求解器,因此该项不包含在函数中。
编写边界条件代码
现在,编写一个函数,该函数返回在边界点处的边界条件的残差值。此函数应具有签名 res = emdenbc(ya,yb),其中:
ya是在区间的开始处的边界条件的值。yb是在区间的结束处的边界条件的值。
对于此问题,一个边界条件针对 ,另一个边界条件针对 。要计算残差值,您需要将边界条件设置为 形式。
在此形式中,边界条件是
,
.
则对应的函数是
function res = emdenbc(ya,yb) res = [ya(2) yb(1) - sqrt(3)/2]; end
创建初始估计值
最后,创建解的初始估计值。对于此问题,使用满足边界条件的常量初始估计值,以及包含介于 0 和 1 之间的五个点的简单网格。没有必要使用许多网格点,因为 BVP 求解器会在求解过程中调整这些点。
,
.
guess = [sqrt(3)/2; 0]; xmesh = linspace(0,1,5); solinit = bvpinit(xmesh, guess);
求解方程
为 S 创建矩阵,并将其作为 'SingularTerm' 选项的值传递给 bvpset。最后,使用 ODE 函数、边界条件函数、初始估计值和 options 结构体调用 bvp4c。
S = [0 0; 0 -2];
options = bvpset('SingularTerm',S);
sol = bvp4c(@emdenode, @emdenbc, solinit, options);对解进行绘图
计算 中解析解的值。
x = linspace(0,1); truy = 1 ./ sqrt(1 + (x.^2)/3);
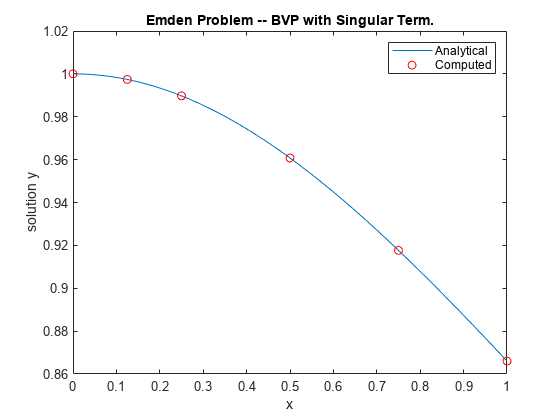
绘制解析解和 bvp4c 计算的解,以进行比较。
plot(x,truy,sol.x,sol.y(1,:),'ro'); title('Emden Problem -- BVP with Singular Term.') legend('Analytical','Computed'); xlabel('x'); ylabel('solution y');
局部函数
此处列出了 BVP 求解器 bvp4c 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。
function dydx = emdenode(x,y) % equation being solved dydx = [y(2) -y(1)^5]; end %------------------------------------------- function res = emdenbc(ya,yb) % boundary conditions res = [ya(2) yb(1) - sqrt(3)/2]; end %-------------------------------------------
另请参阅
bvp4c | bvp5c | bvpinit | bvpset