nufft
非均匀快速傅里叶变换
说明
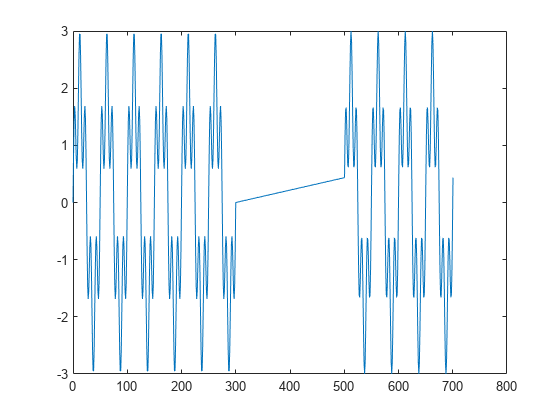
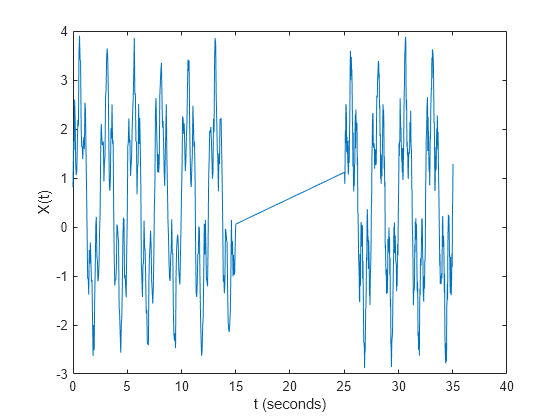
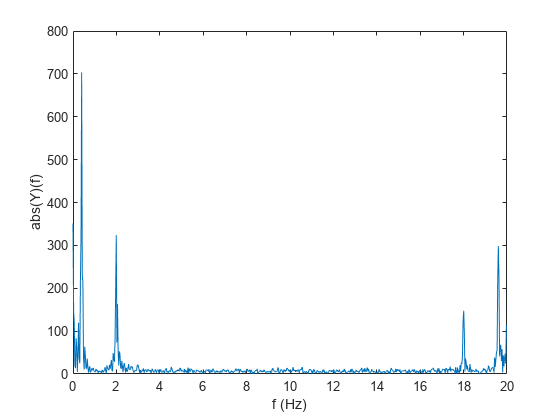
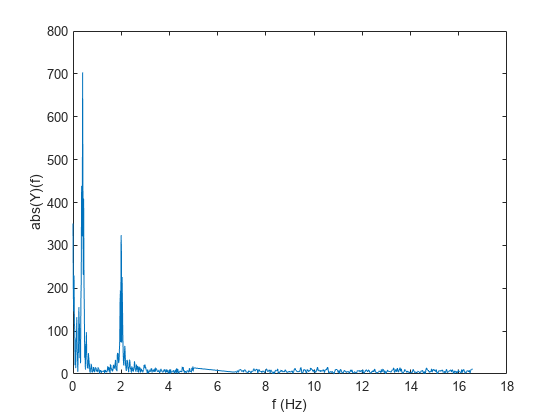
Y = nufft(X,t)t 返回 X 的非均匀离散傅里叶变换 (NUDFT)。
如果
X是向量，则nufft返回该向量的变换。如果
X是矩阵，则nufft将X的各列视为向量，并返回每列的变换。如果
X是一个多维数组，则nufft将沿大小不等于 1 的第一个数组维度的值视为向量，并返回每个向量的变换。
Y = nufft(X)X 的离散傅里叶变换，等效于 fft(X)。
示例
创建在非均匀分布的点 t 上采样的信号 X。绘制信号。
t = [0:300 500.5:700.5]; S = 2*sin(2*pi*0.02*t) + sin(2*pi*0.1*t); X = S + rand(size(t)); plot(t,X)
求信号的非均匀快速傅里叶变换。当您使用 nufft 而没有提供频率作为第三个参量时，nufft 将使用默认频率缩放，其中对于信号长度 n，频率采用 f(i) = (i-1)/n 形式。将变换的绝对值绘制为默认频率的函数。
Y = nufft(X,t); n = length(t); f = (0:n-1)/n; plot(f,abs(Y))
创建一个由非均匀采样点组成的时间向量。为等效均匀采样数据定义约 35 秒的持续时间，采样周期 T = 50 毫秒（或采样频率 Fs = 20 Hz）。
T = 50e-3; % Sampling period of 50 ms for equivalent uniform samples Fs = 1/T; % Sampling frequency of 20 Hz for equivalent uniform samples t = [0:T:300*T 500.5*T:T/2:700.5*T];
创建一个信号 X，在非等间距点 t 处进行采样，峰值频率为 0.4 Hz 和 2 Hz。
S = 2*sin(2*pi*0.4*t) + sin(2*pi*2*t); % Signal with peak frequencies at 0.4 Hz and 2 Hz X = S + rand(size(t)); plot(t,X) xlabel("t (seconds)") ylabel("X(t)")
求信号的非均匀快速傅里叶变换。使用 nufft（而不提供频率）作为第三个参量。在本例中，对于信号长度 n，nufft 使用 f(i) = (i-1)/n 形式的默认频率。对于等效均匀采样数据，非均匀离散傅里叶变换将非均匀采样点 t 和频率 f 视为采样周期为 1 秒、采样频率为 1 Hz。因此，当使用 nufft 获取具有正确缩放单位的变换时，请将缩放因子 T 包括到时间向量中。将变换的绝对值绘制为按 Fs 缩放的默认频率的函数。
Y = nufft(X,t/T); n = length(t); f = (0:n-1)/n*Fs; plot(f,abs(Y)) xlabel("f (Hz)") ylabel("abs(Y)(f)")
当使用 nufft 时，还可以指定非均匀频率向量或查询点 f 作为第三个参量，非均匀时间向量 t 作为第二个参量。此处，当使用 nufft 时，不需要重新缩放 t 和 f。将变换的绝对值绘制为非均匀频率的函数。
f = [0:0.5:n/4 n/3+1:n-120]/n*Fs; Y = nufft(X,t,f); plot(f,abs(Y)) xlabel("f (Hz)") ylabel("abs(Y)(f)")
定义和标注一系列音乐音调的频率。
C3 = 440 / (2^(21/12)); nOctaves = 3; musicalTones = C3 * 2.^((0:(12*nOctaves-1))/12); toneNames = ["C";"C#";"D";"D#";"E";"F";"F#";"G";"G#";"A";"A#";"B"] + string(3:(3+nOctaves-1)); toneNames = categorical(toneNames, toneNames);
定义以 Hz 为单位的音频信号采样频率，采样点为 n 个，以及包含主和弦 X 的信号。
fs = 16e3; n = 1:16000; X = 4*cos(2*pi*(440/fs)*n) + 2*cos(2*pi*(554.37/fs)*n) + 3*cos(2*pi*(659.2/fs)*n);
计算并绘制主和弦的频率分量。
Y = nufft(X,[],musicalTones/fs); bar(toneNames(:),abs(Y))
输入参数
详细信息
参考
[1] Potter, Samuel F., Nail A. Gumerov, and Ramani Duraiswami. “Fast Interpolation of Bandlimited Functions.” In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 4516–20. New Orleans, LA: IEEE, 2017. https://doi.org/10.1109/ICASSP.2017.7953011.
[2] Dutt, A., and V. Rokhlin. “Fast Fourier Transforms for Nonequispaced Data.” SIAM Journal on Scientific Computing 14, no. 6 (November 1993): 1368–93. https://doi.org/10.1137/0914081.
扩展功能
版本历史记录
在 R2020a 中推出
