trenddecomp
Syntax
Description
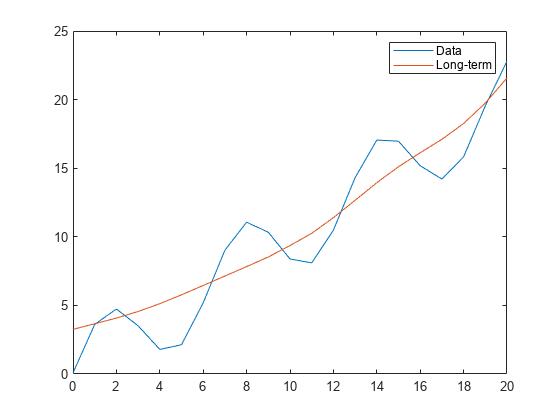
LT = trenddecomp(A)A = LT+ST+R. In this
decomposition, LT is the long-term trend in the data,
ST is the seasonal, or oscillatory, trend (or trends), and
R is the remainder. LT is a vector with the same
length as A.
SSA is a useful algorithm when the periods of the seasonal trends are unknown. The SSA algorithm assumes that the input data is uniformly spaced.
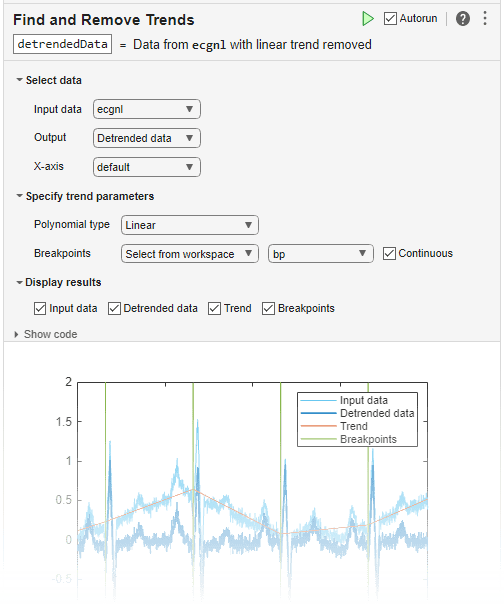
You can use trenddecomp functionality interactively by adding the
Find and Remove
Trends task to a live script.
LT = trenddecomp(A,"ssa",lag)A and additionally
specifies a lag value, which determines the size of the matrix on which the singular value
decomposition is computed, as described in [1]. Larger values of
lag typically result in more separation of the trends.
The value of lag must be a scalar in the interval
[3,N/2] where N is the length of
A. If the period of the seasonal trend is known, then specify
lag as a multiple of the period.
LT = trenddecomp(A,"stl",period)A through seasonal trend decomposition using Loess
(STL), which is an additive decomposition based on a locally weighted regression, as
described in [2]. STL requires a period for the
seasonal trend. When the data has only one seasonal trend, specify
period as a scalar value. For multiple seasonal trends, specify
period as a vector whose elements are the periods for each seasonal
trend.
The STL algorithm assumes that the input data is uniformly spaced.
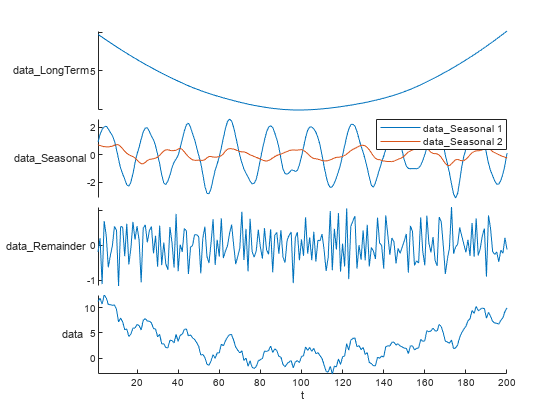
D = trenddecomp(T)trenddecomp
operates on each table variable separately. D is a table or timetable
whose variables contain the long-term trend, seasonal trends, and remainder for each
variable. trenddecomp returns multiple seasonal trends as one variable
in D, whose columns contain each seasonal trend.
Examples
Input Arguments
Output Arguments
Tips
An additive decomposition model is appropriate for data where the seasonal variation is relatively constant throughout the time series. If the seasonal variation is proportional to the level of the time series, to use an additive decomposition model, use a log transformation on the data before the decomposition.
Alternative Functionality
Live Editor Task
You can use trenddecomp functionality interactively by adding the
Find and Remove
Trends task to a live script.
References
[1] Golyandina, Nina, and Anatoly Zhigljavsky. Singular Spectrum Analysis for Time Series. SpringerBriefs in Statistics. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013. https://doi.org/10.1007/978-3-642-34913-3.
[2] Cleveland, R.B., W.S. Cleveland, J.E. McRae, and I. Terpenning. “STL: A Seasonal-Trend Decomposition Procedure Based on Loess.” Journal of Official Statistics 6 (1990): 3–73.
Version History
Introduced in R2021b