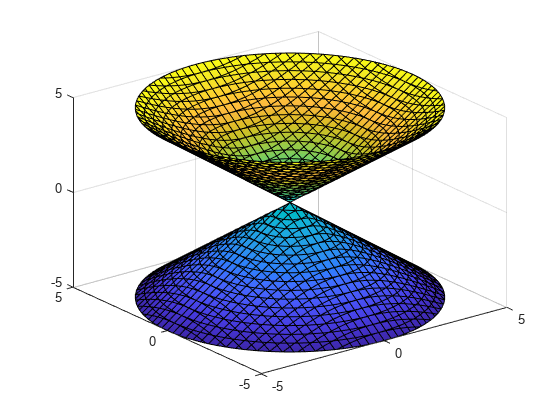
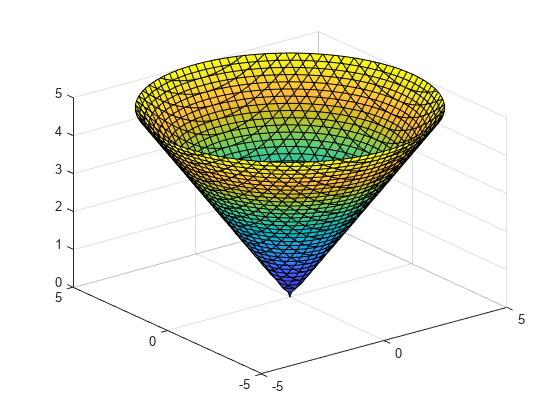
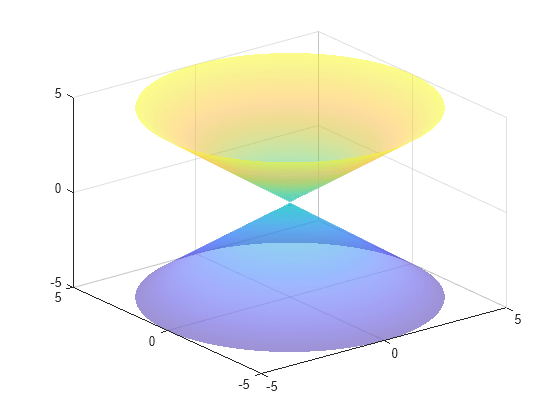
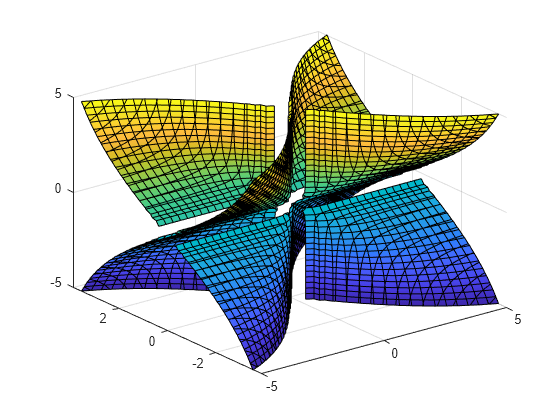
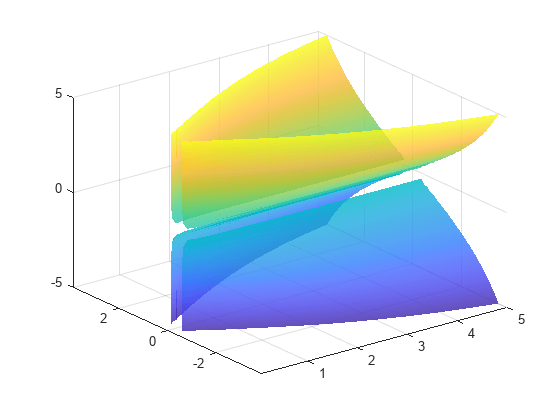
fimplicit3
绘制三维隐函数
语法
说明
fimplicit3( 将在 ax,___)ax 指定的坐标区中，而不是在当前坐标区中绘制图形。将坐标区指定为第一个输入参量，先于上述任何输入参量。
fimplicit3(___, 指定线型、标记符号和线条颜色。例如，LineSpec)'-r' 指定红色线条。
fimplicit3(___, 使用一个或多个名称-值对组参量指定曲面属性。例如，Name,Value)'FaceAlpha',0.6 为半透明曲面指定透明度值 0.6。
fs = fimplicit3(___)ImplicitFunctionSurface 对象。使用 fs 可在创建曲面后访问和修改曲面的属性。有关属性列表，请参阅 ImplicitFunctionSurface 属性。
示例
在 x、y 和 z 的默认区间 绘制双曲面 。
f = @(x,y,z) x.^2 + y.^2 - z.^2; fimplicit3(f)
对于 z，通过将绘图区间指定为 [0 5]，绘制双曲面 的上半部分。对于 x 和 y，使用默认区间 [-5 5]。
f = @(x,y,z) x.^2 + y.^2 - z.^2; interval = [-5 5 -5 5 0 5]; fimplicit3(f,interval)
绘制隐曲面 。通过将 EdgeColor 属性设置为 'none' 删除线条。通过将 FaceAlpha 属性设置为 0 到 1 之间的值添加透明度。
f = @(x,y,z) x.^2 + y.^2 - z.^2; fimplicit3(f,'EdgeColor','none','FaceAlpha',.5)
绘制隐曲面并将隐曲面对象赋给变量 fs。
f = @(x,y,z) 1./x.^2 - 1./y.^2 + 1./z.^2; fs = fimplicit3(f)
fs =
ImplicitFunctionSurface with properties:
Function: @(x,y,z)1./x.^2-1./y.^2+1./z.^2
EdgeColor: [0 0 0]
LineStyle: '-'
FaceColor: 'interp'
Show all properties
使用 fs 在创建隐曲面后访问和修改其属性。例如，通过将 XRange 属性设置为 [0 5]，只显示正 x 值。通过将 EdgeColor 属性设置为 'none' 删除线条。通过将 FaceAlpha 属性设置为 0.8 添加透明度。
fs.XRange = [0 5];
fs.EdgeColor = 'none';
fs.FaceAlpha = 0.8;
输入参数
要绘制的三维隐函数，指定为命名或匿名函数的函数句柄。
指定 w = f(x,y,z) 形式的函数。该函数必须接受三个三维数组输入参量，并返回大小相同的三维数组输出参量。为获得最佳性能，应使用数组运算符而不是矩阵运算符。例如，使用 .* (times) 而不是 * (mtimes)。
示例: fimplicit3(@(x,y,z) x.^2 + y.^2 - z.^2)
x、y 和 z 的绘图区间，指定为下列形式之一：
[min max]形式的二元素向量 - 对x、y和z使用相同的绘图区间[min max]。[xmin xmax ymin ymax zmin zmax]形式的六元素向量 - 对x、y和z使用不同绘图区间。在区间[xmin xmax]（对于x）、[ymin ymax]（对于y）和[zmin zmax]（对于z）上绘图。
示例: fimplicit3(f,[-2 3 -4 5 -3 3])
线型、标记和颜色，指定为包含符号的字符串标量或字符向量。符号可以按任意顺序显示。您不需要同时指定所有三个特征（线型、标记和颜色）。例如，如果忽略线型，只指定标记，则绘图只显示标记，不显示线条。
示例: "--or" 是带有圆形标记的红色虚线。
| 线型 | 描述 | 表示的线条 |
|---|---|---|
"-" | 实线 |
|
"--" | 虚线 |
|
":" | 点线 |
|
"-." | 点划线 |
|
| 标记 | 描述 | 生成的标记 |
|---|---|---|
"o" | 圆圈 |
|
"+" | 加号 |
|
"*" | 星号 |
|
"." | 点 |
|
"x" | 叉号 |
|
"_" | 水平线条 |
|
"|" | 垂直线条 |
|
"square" | 方形 |
|
"diamond" | 菱形 |
|
"^" | 上三角 |
|
"v" | 下三角 |
|
">" | 右三角 |
|
"<" | 左三角 |
|
"pentagram" | 五角形 |
|
"hexagram" | 六角形 |
|
| 颜色名称 | 短名称 | RGB 三元组 | 外观 |
|---|---|---|---|
"red" | "r" | [1 0 0] |
|
"green" | "g" | [0 1 0] |
|
"blue" | "b" | [0 0 1] |
|
"cyan" | "c" | [0 1 1] |
|
"magenta" | "m" | [1 0 1] |
|
"yellow" | "y" | [1 1 0] |
|
"black" | "k" | [0 0 0] |
|
"white" | "w" | [1 1 1] |
|
坐标区对象。如果您不指定坐标区，则 fimplicit3 使用当前坐标区。
名称-值参数
以 Name1=Value1,...,NameN=ValueN 的形式指定可选参量对组，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。
在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。
示例: fimplicit3(f,'MeshDensity',50,'FaceAlpha',0.5) 指定计算点数和透明度值。
此处所列的 ImplicitFunctionSurface 属性只是一部分。有关完整列表，请参阅 ImplicitFunctionSurface 属性。
每个方向上的计算点数，指定为标量。
面颜色，指定为 'interp'、RGB 三元组、十六进制颜色代码、颜色名称或短名称。默认值 'interp' 将基于 ZData 的值进行颜色插值。
对于自定义颜色，请指定 RGB 三元组或十六进制颜色代码。
RGB 三元组是包含三个元素的行向量，其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内，例如[0.4 0.6 0.7]。十六进制颜色代码是字符串标量或字符向量，以井号 (
#) 开头，后跟三个或六个十六进制数字，范围可以是0到F。这些值不区分大小写。因此，颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外，还可以按名称指定一些常见的颜色。下表列出了一些命名颜色选项、其等效 RGB 三元组及十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | 不适用 | 不适用 | 不适用 | 无颜色 |
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如，获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
线条颜色，指定为 'interp'、RGB 三元组、十六进制颜色代码、颜色名称或短名称。默认的 RGB 三元组值 [0 0 0] 与黑色对应。值 'interp' 将基于 ZData 的值为边着色。
对于自定义颜色，请指定 RGB 三元组或十六进制颜色代码。
RGB 三元组是包含三个元素的行向量，其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内，例如[0.4 0.6 0.7]。十六进制颜色代码是字符串标量或字符向量，以井号 (
#) 开头，后跟三个或六个十六进制数字，范围可以是0到F。这些值不区分大小写。因此，颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外，还可以按名称指定一些常见的颜色。下表列出了一些命名颜色选项、其等效 RGB 三元组及十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | 不适用 | 不适用 | 不适用 | 无颜色 |
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如，获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
线型，指定为下表中列出的选项之一。
| 线型 | 描述 | 表示的线条 |
|---|---|---|
"-" | 实线 |
|
"--" | 虚线 |
|
":" | 点线 |
|
"-." | 点划线 |
|
"none" | 无线条 | 无线条 |
提示
为了获得最佳性能和避免产生警告消息，请使用按元素运算符。例如，使用
x.*y而不是x*y。有关详细信息，请参阅数组与矩阵运算。放大图形时，
fimplicit3将重新计算数据，这样可以显示隐藏的详细信息。
版本历史记录
在 R2016b 中推出
