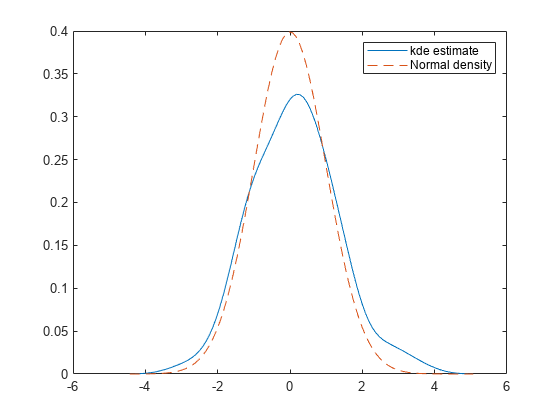
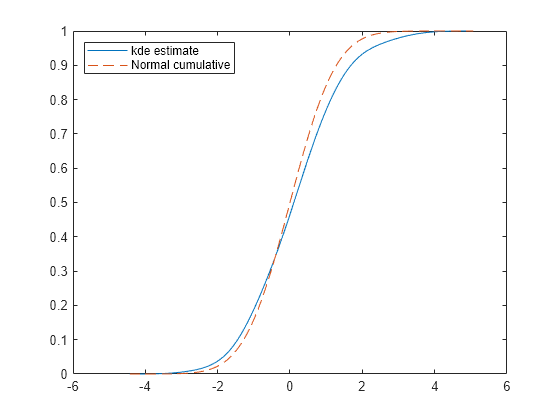
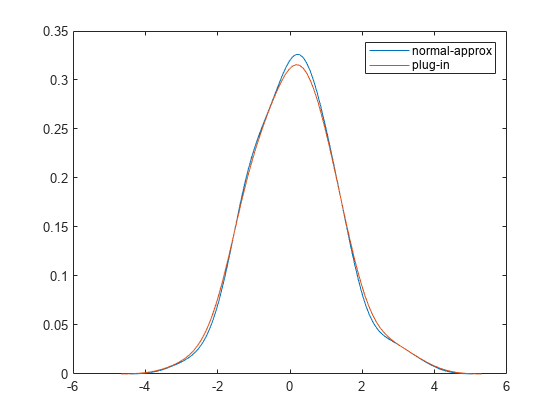
kde

单变量数据的核密度估计值

自 R2023b 起

全页折叠

语法

[f,xf] = kde(a)

[f,xf,bw] = kde(a)

[___] = kde(a,Name=Value)

说明

[f,xf] = kde(a) 估计向量 a 中单变量数据的概率密度函数 (pdf)，并返回在计算点 xf 处估计的 pdf 的值 f。kde 使用核密度估计值来估计 pdf。有关详细信息，请参阅核分布。

示例

[f,xf,bw] = kde(a) 还返回核平滑函数的带宽。

示例

[___] = kde(a,Name=Value) 使用一个或多个名称-值参量指定选项。例如，kde(a,ProbabilityFcn="cdf") 估计 a 的累积分布函数 (cdf) 而不是 pdf。可以将此语法与上述语法中的任何输出参量结合使用。

示例

全部折叠

估计概率函数

打开实时脚本

生成一些正态分布数据。

rng(0,"twister") %  For reproducibility
a = randn(100,1);

估计样本数据的 pdf。

[fp,xfp] = kde(a);

fp 包含估计的 pdf 在 xfp 中的计算点处的值。

估计样本数据的 cdf。

[fc,xfc] = kde(a,ProbabilityFcn="cdf");

fc 包含估计的 cdf 在 xfc 中的计算点处的值。xfc 和 xfp 包含相同的计算点，因为它们都是使用 a 中的样本数据计算的。

在计算点处计算正态分布的 pdf 和 cdf。

np = (1/sqrt(2*pi))*exp(-.5*(xfp.^2));
nc = 0.5*(1+erf(xfc/sqrt(2)));

绘制估计的 pdf 与正态分布 pdf 的对比图。

plot(xfp,fp,"-",xfp,np,"--")
legend("kde estimate","Normal density")

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent kde estimate, Normal density.

绘制估计的 pdf 与正态分布 pdf 的对比图。

figure
plot(xfc,fc,"-",xfc,nc,"--")
legend("kde estimate","Normal cumulative",Location="northwest")

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent kde estimate, Normal cumulative.

绘图显示，估计的 pdf 和 cdf 的形状与标准正态分布的 pdf 和 cdf 的形状相似。

检查带宽

打开实时脚本

生成一些正态分布数据。

rng(0,"twister") %  For reproducibility
a = randn(100,1);

估计样本数据的 pdf。默认情况下，kde 使用正态逼近方法计算核平滑函数的带宽。

[fn,xfn,bwn] = kde(a);

fn 包含估计的 pdf 在 xfn 中的计算点处的值，bwn 是核平滑函数的带宽。

使用插入法估计 pdf，并显示与每个估计的 pdf 关联的带宽。

[p,xp,bwp] = kde(a,Bandwidth="plug-in");
[bwn,bwp]

ans = 1×2

    0.4958    0.5751

使用正态逼近方法计算的带宽小于使用插入法计算的带宽。

绘制估计的 pdf。

plot(xfn,fn)
hold on
plot(xp,p)
legend("normal-approx","plug-in")

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent normal-approx, plug-in.

估计的 pdf 具有正态分布的典型形状。与正态逼近方法对应的 pdf 峰值高于与插入法对应的 pdf 峰值。

比较核平滑器

打开实时脚本

生成一些双峰样本数据。

rng(0,"twister") %  For reproducibility
a = [randn(100,1)-5; randn(20,1)+5];

使用默认 "normal" 核平滑函数估计样本数据的 pdf。使用 "box"、"triangle" 和 "parabolic" 核平滑函数计算 pdf 的另外三个估计值。

[f1,xf1] = kde(a);
[f2,xf2] = kde(a,Kernel="box");
[f3,xf3] = kde(a,Kernel="triangle");
[f4,xf4] = kde(a,Kernel="parabolic");

xf1、xf2、xf3 和 xf4 包含相同的计算点，因为它们都是使用 a 中的样本数据计算的。f1、f2、f3 和 f4 包含每个估计的 pdf 在计算点处的值。

绘制估计的 pdf。

tiledlayout(2,2)
nexttile
plot(xf1,f1) %  normal
nexttile
plot(xf2,f2) %  box
nexttile
plot(xf3,f3) %  triangle
nexttile
plot(xf4,f4) %  parabolic

Figure contains 4 axes objects. Axes object 1 contains an object of type line. Axes object 2 contains an object of type line. Axes object 3 contains an object of type line. Axes object 4 contains an object of type line.

绘图显示，四个估计的 pdf 具有相似的垂直范围，且每个估计的 pdf 有两个峰值。使用 "box" 核计算的 pdf 在四个估计的 pdf 中显得最不平滑。

输入参数

全部折叠

`a` — 样本数据
数值向量

用于估计概率函数的样本数据，指定为数值向量。

数据类型: single | double

名称-值参数

全部折叠

将可选参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

示例: kde(a,Kernel="box",Bandwidth=0.8,Weight=wgt) 指定带宽为 0.8、观测值权重向量为 wgt 的箱型核平滑函数。

`Bandwidth` — 核平滑函数的带宽
`"normal-approx"` (默认) | `"plug-in"` | 正标量

核平滑函数的带宽，指定为 "normal-approx"、"plug-in" 或正标量。

当 Bandwidth 为 "normal-approx" 时，kde 使用正态逼近方法或 Silverman 经验法则计算带宽。
当 Bandwidth 为 "plug-in" 时，kde 使用 [1] 中所述的改进插入法计算带宽。插入法有时称为 Sheather-Jones 法。
当 Bandwidth 为正标量时，其值控制概率函数估计的平滑度。随着值的增大，概率函数估计变得更平滑。

要了解 Bandwidth 如何影响核平滑函数，请参阅 Kernel。

示例: kde(a,Bandwidth="plug-in")

数据类型: single | double | string | char

`EvaluationPoints` — 计算估计概率函数的点
数值向量

计算估计概率函数的点，指定为数值向量。默认情况下，kde 在 NumPoints 个等距点处计算估计的概率函数，这些点覆盖 a 中观测值的范围。

如果同时指定 NumPoints 和 EvaluationPoints 名称-值参量，kde 将忽略 NumPoints。

示例: kde(a,EvaluationPoints=linspace(0,10,50))

数据类型: single | double

`Kernel` — 核平滑函数的类型
`"normal"` (默认) | `"box"` | `"triangle"` | `"parabolic"` | 函数句柄

核平滑函数的类型，指定为函数句柄或下表中的值之一。

值	方程
`"normal"`	$K_{i} (x) = \frac{1}{\sqrt{2 π}} e^{\frac{- d_{i}^{2}}{2}}$
`"box"`	$K_{i} (x) = {\begin{matrix} \frac{1}{2 \sqrt{3}}, \| d_{i} \| \leq \sqrt{3} \\ 0, \| d_{i} \| > \sqrt{3} \end{matrix}$
`"triangle"`	$K_{i} (x) = {\begin{matrix} \frac{1 - \frac{\| d_{i} \|}{\sqrt{6}}}{\sqrt{6}}, \| d_{i} \| \leq \sqrt{6} \\ 0, \| d_{i} \| > \sqrt{6} \end{matrix}$
`"parabolic"`	$\begin{array}{l} K_{i, h} (x) = \max (0, \frac{3}{4} u), \\ u = \frac{1 - \frac{z^{2}}{5}}{\sqrt{5}}, \\ z = \max (- \sqrt{5}, \min (d_{i}, \sqrt{5})) \end{array}$

在该表中， $d_{i} = \frac{x - a_{i}}{h}$ ，其中 h 是在 Bandwidth 名称-值参量中指定的带宽，a_i 是 a 中位置 i 处的元素。如果某个随机变量的 pdf 由该表中的一个核定义，则该随机变量的方差为 1。抛物线核平滑函数有时称为依潘涅契科夫平滑函数。

如果将 Kernel 指定为函数句柄，则该函数必须接受任意长度的矩阵或列向量作为其唯一输入参量，并返回相同大小的非负矩阵或向量。

有关 kde 如何使用核平滑函数估计概率函数的详细信息，请参阅核分布。

示例: kde(a,Kernel="parabolic")

数据类型: string | char | function_handle

`NumPoints` — 计算点数
正整数标量

估计概率函数的计算点数量，指定为正整数标量。默认情况下，NumPoints = max(100,u)，其中 u 是 a 中元素数的平方根，舍入到最接近的整数。

如果同时指定 NumPoints 和 EvaluationPoints 名称-值参量，kde 将忽略 NumPoints。

示例: kde(a,NumPoints=100)

数据类型: single | double

`ProbabilityFcn` — 概率函数
`"pdf"` (默认) | `"cdf"`

要估计的概率函数，指定为 "pdf" 或 "cdf"。当 ProbabilityFcn 为 "pdf" 时，kde 估计概率密度函数。要估计累积分布函数，请将 ProbabilityFcn 指定为 "cdf"。

示例: kde(a,ProbabilityFcn="cdf")

`Support` — 样本数据的区间
`"unbounded"` (默认) | `"positive"` | `"nonnegative"` | `"negative"` | 二元素数值向量

样本数据的区间，指定为二元素数值向量、"unbounded"、"positive"、"nonnegative" 或 "negative"。a 的元素必须在由 Support 指定的区间内。估计概率函数在该区间外的计算结果为 0。

如果将 Support 指定为二元素向量 [L U] 或 [L;U]，则 L 必须小于 min(a)，且 U 必须大于 max(a)。该区间是开区间，下界为 L，上界为 U。

如果将 Support 指定为字符串，则样本数据存在于下表描述的区间内。

值	支持
`"unbounded"`	$(- I n f, I n f)$
`"positive"`	$(0, I n f)$
`"nonnegative"`	$[0, I n f)$
`"negative"`	$(- I n f, 0)$

示例: kde(a,Support="nonnegative")

数据类型: single | double | string | char

`Weight` — 观测值权重
非负向量

观测值权重，指定为非负向量。默认情况下，kde 对 a 中的所有观测值进行同等加权。有关 kde 如何使用权重估计概率函数的详细信息，请参阅核分布。

数据类型: single | double

输出参量

全部折叠

`f` — 估计函数值
数值向量

估计函数值，以数值向量形式返回。f 的长度等于 xf 中计算点的数量。

`xf` — 求值点
数值向量

计算点，以数值向量形式返回。如果指定 EvaluationPoints 名称-值参量，则 xf 的大小与 EvaluationPoints 相同。否则，xf 的大小由 NumPoints 名称-值参量给出。

`bw` — 带宽
正标量

核平滑函数的带宽，以正标量形式返回。您可以使用 Bandwidth 名称-值参量来指定 bw 的值或用于计算 bw 的方法。

详细信息

全部折叠

核分布

核分布是一个随机变量的概率密度函数 (pdf) 的非参数化表示。当参数化分布无法正确描述数据或者您想避免对数据分布进行假设时，您可以使用核分布。核分布由平滑函数和带宽值定义，它们控制生成的密度曲线的平滑度。

核估计器是随机变量的估计概率函数。对于 x 的任何实数值，pdf 的核估计器根据

${\hat{f}}_{h} (x) = \frac{1}{n h} \sum_{i = 1}^{n} w_{i} K (\frac{x - x_{i}}{h}),$

计算，其中 x_i 值来自未知分布的随机样本，w_i 值是它们对应的权重，n 是样本大小， $K$ 是核平滑函数，h 是带宽。

对于 x 的任何实数值，累积分布函数 (cdf) 的核估计器根据下式计算：

${\hat{F}}_{h} (x) = \int_{- \infty}^{x} {\hat{f}}_{h} (t) d t = \frac{1}{n h} \sum_{i = 1}^{n} w_{i} G (\frac{x - x_{i}}{h}),$

其中 $G (x) = \int_{- \infty}^{x} K (t) d t$ 。

有关详细信息，请参阅Kernel Distribution (Statistics and Machine Learning Toolbox)。

参考

[1] Botev, Z. I., J. F. Grotowski, and D. P. Kroese. "Kernel Density Estimation via Diffusion." The Annals of Statistics, vol. 38, no. 5 (October 1, 2010). https://projecteuclid.org/journals/annals-of-statistics/volume-38/issue-5/Kernel-density-estimation-via-diffusion/10.1214/10-AOS799.full

[2] Bowman, A. W., and A. Azzalini. "Applied Smoothing Techniques for Data Analysis." New York: Oxford University Press Inc., 1997.

[3] Hill, P. D. "Kernel estimation of a distribution function." Communications in Statistics - Theory and Methods. 14, no. 3(January 1985): 605–620.

[4] Jones, M. C. "Simple boundary correction for kernel density estimation." Statistics and Computing. no. 3(September 1993): 135–146.

[5] Silverman, B. W. "Density Estimation for Statistics and Data Analysis." Chapman & Hall/CRC, 1986.

版本历史记录

在 R2023b 中推出

另请参阅

函数

histogram | histcounts (Statistics and Machine Learning Toolbox) | ksdensity (Statistics and Machine Learning Toolbox)

主题

Kernel Distribution (Statistics and Machine Learning Toolbox)
Nonparametric and Empirical Probability Distributions (Statistics and Machine Learning Toolbox)

kde

语法

说明

示例

估计概率函数

检查带宽

比较核平滑器

输入参数

a — 样本数据 数值向量

名称-值参数

Bandwidth — 核平滑函数的带宽 "normal-approx" (默认) | "plug-in" | 正标量

EvaluationPoints — 计算估计概率函数的点 数值向量

Kernel — 核平滑函数的类型 "normal" (默认) | "box" | "triangle" | "parabolic" | 函数句柄

NumPoints — 计算点数 正整数标量

ProbabilityFcn — 概率函数 "pdf" (默认) | "cdf"

Support — 样本数据的区间 "unbounded" (默认) | "positive" | "nonnegative" | "negative" | 二元素数值向量

Weight — 观测值权重 非负向量

输出参量

f — 估计函数值 数值向量

xf — 求值点 数值向量

bw — 带宽 正标量

详细信息

核分布

参考

版本历史记录

另请参阅

函数

主题

`a` — 样本数据
数值向量

`Bandwidth` — 核平滑函数的带宽
`"normal-approx"` (默认) | `"plug-in"` | 正标量

`EvaluationPoints` — 计算估计概率函数的点
数值向量

`Kernel` — 核平滑函数的类型
`"normal"` (默认) | `"box"` | `"triangle"` | `"parabolic"` | 函数句柄

`NumPoints` — 计算点数
正整数标量

`ProbabilityFcn` — 概率函数
`"pdf"` (默认) | `"cdf"`

`Support` — 样本数据的区间
`"unbounded"` (默认) | `"positive"` | `"nonnegative"` | `"negative"` | 二元素数值向量

`Weight` — 观测值权重
非负向量

`f` — 估计函数值
数值向量

`xf` — 求值点
数值向量

`bw` — 带宽
正标量