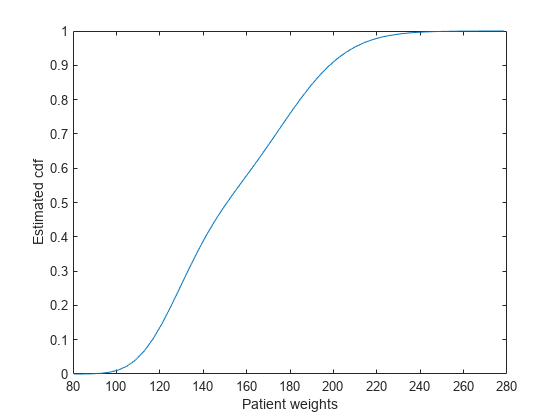
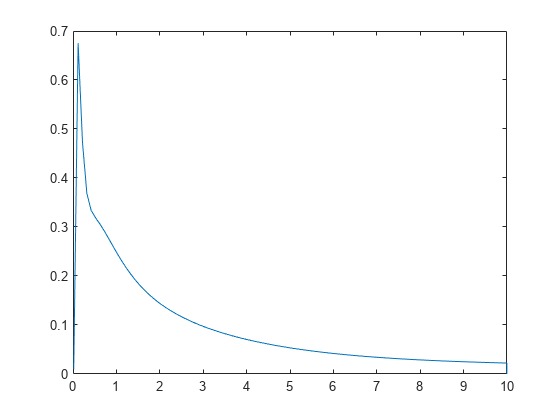
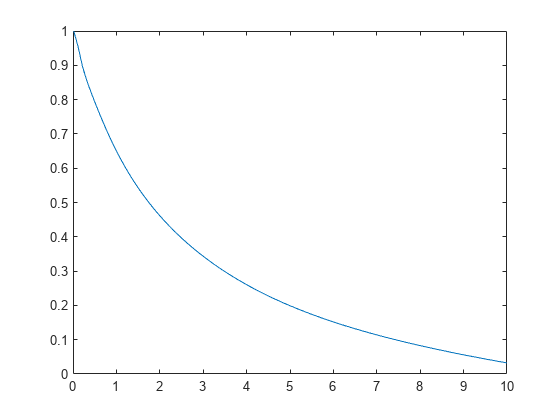
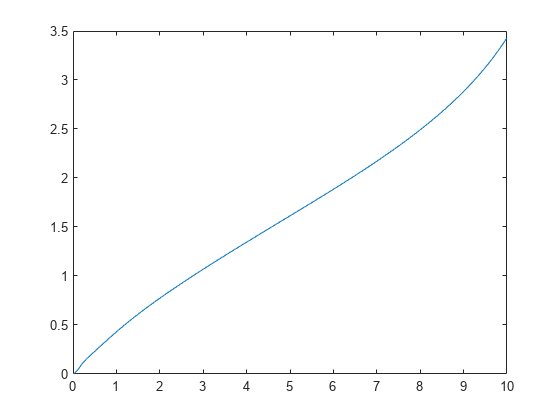
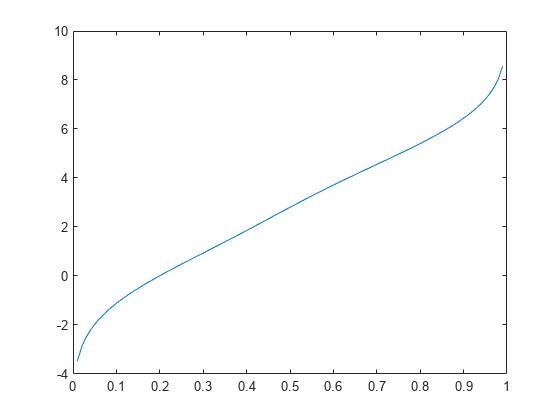
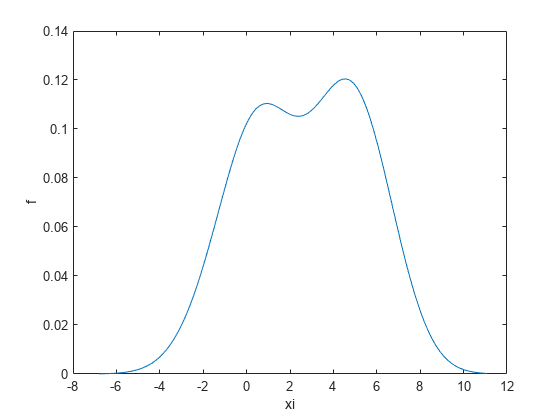
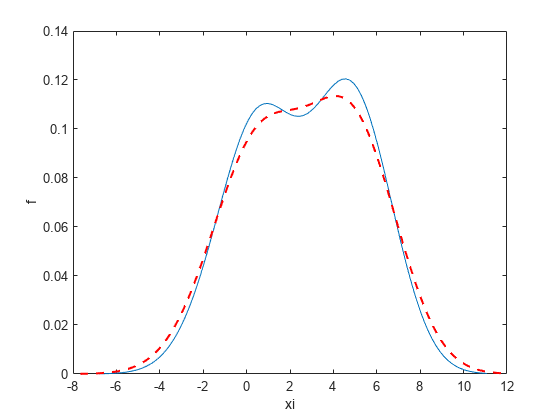
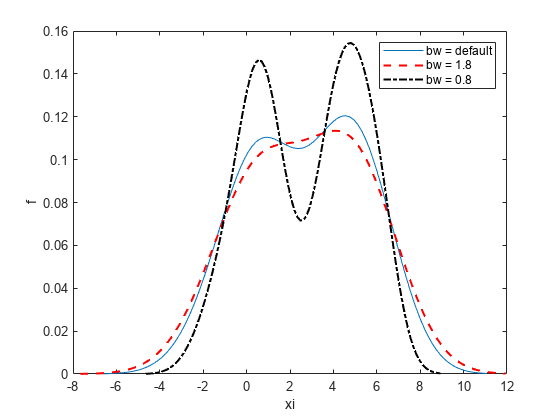
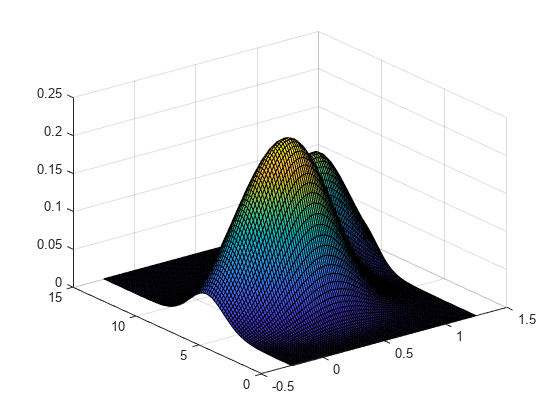
ksdensity
用于一元数据和二元数据的核平滑函数估计
语法
说明
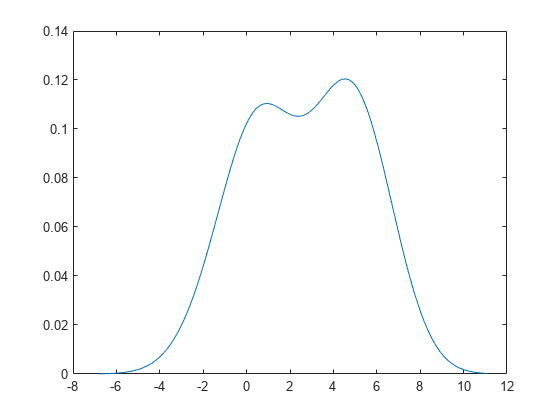
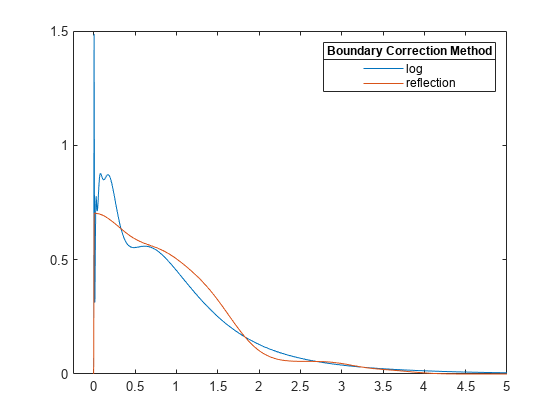
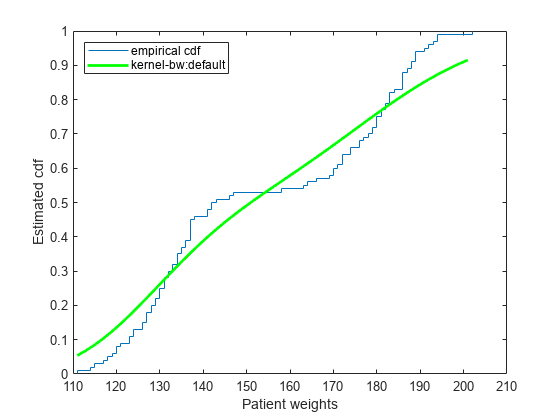
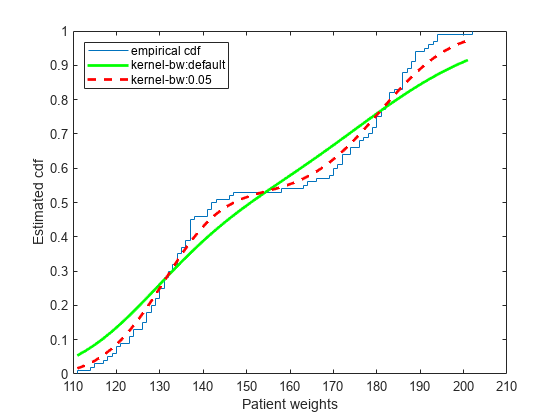
示例
输入参数
名称-值参数
输出参量
详细信息
替代功能
您也可以使用 MATLAB® kde 函数来估计一元数据的 pdf 或 cdf。与 ksdensity 不同,kde 不支持边界校正方法或数据删失。
参考
[1] Botev, Z. I., J. F. Grotowski, and D. P. Kroese. "Kernel Density Estimation via Diffusion." The Annals of Statistics, vol. 38, no. 5 (October 1, 2010). https://projecteuclid.org/journals/annals-of-statistics/volume-38/issue-5/Kernel-density-estimation-via-diffusion/10.1214/10-AOS799.full
[2] Bowman, A. W., and A. Azzalini. Applied Smoothing Techniques for Data Analysis. New York: Oxford University Press Inc., 1997.
[3] Hill, P. D. “Kernel estimation of a distribution function.” Communications in Statistics - Theory and Methods. Vol 14, Issue. 3, 1985, pp. 605-620.
[4] Jones, M. C. “Simple boundary correction for kernel density estimation.” Statistics and Computing. Vol. 3, Issue 3, 1993, pp. 135-146.
[5] Silverman, B. W. Density Estimation for Statistics and Data Analysis. Chapman & Hall/CRC, 1986.
扩展功能
版本历史记录
在 R2006a 之前推出