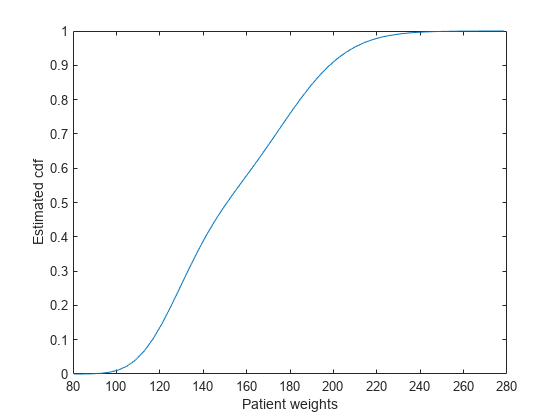
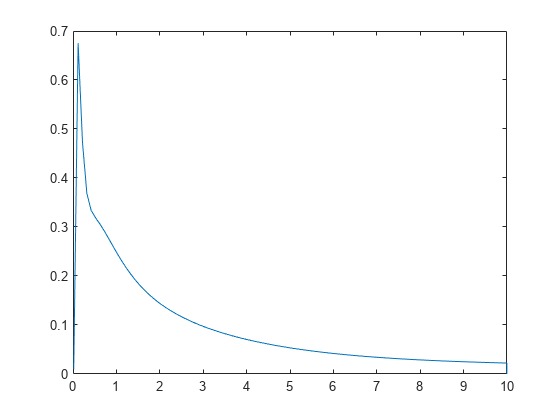
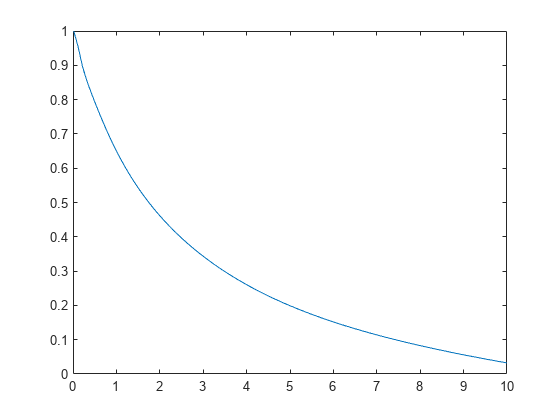
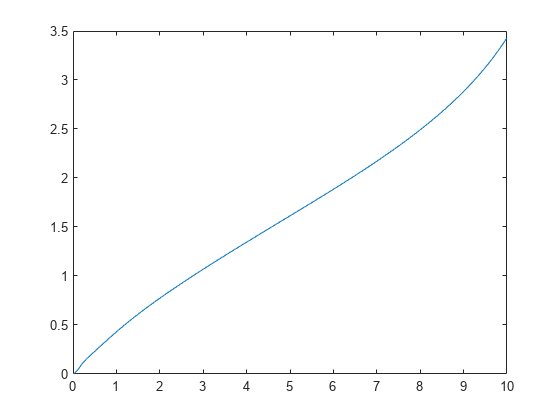
ksdensity

用于一元数据和二元数据的核平滑函数估计

全页折叠

语法

[f,xi] = ksdensity(x)
[f,xi] = ksdensity(x,pts)
[f,xi] = ksdensity(___,Name,Value)
[f,xi,bw] = ksdensity(___)
ksdensity(___)
ksdensity(ax,___)

说明

[f,xi] = ksdensity(x) 返回向量或两列矩阵 x 中样本数据的概率密度估计 f。该估计基于正态核函数，并且是在等间距点 xi 处进行估计的，这些点覆盖 x 中数据的范围。ksdensity 为一元数据估计 100 个点处的密度，或为二元数据估计 900 个点处的密度。

ksdensity 最适合连续分布的样本。

示例

[f,xi] = ksdensity(x,pts) 指定点 (pts) 以计算 f。此处，xi 和 pts 包含相同的值。

示例

[f,xi] = ksdensity(___,Name,Value) 支持上述语法中的任何输入参量，且可使用一个或多个名称-值对组参量指定的其他选项。例如，您可以定义 ksdensity 计算的函数类型，例如概率密度、累积概率、生存函数等。您也可以指定平滑窗的带宽。

示例

[f,xi,bw] = ksdensity(___) 还返回核平滑窗的带宽 bw。对于正态密度而言，默认带宽是最优的。

示例

ksdensity(___) 绘制核平滑函数估计。

示例

ksdensity(ax,___) 使用带句柄 ax 的坐标区绘制结果，而不是 gca 返回的当前坐标区。

示例

全部折叠

打开实时脚本

从两个正态分布的混合生成样本数据集。 

rng('default')  % For reproducibility
x = [randn(30,1); 5+randn(30,1)];

绘制估计密度。 

[f,xi] = ksdensity(x); 
figure
plot(xi,f);

Figure contains an axes object. The axes object contains an object of type line.

密度估计显示样本呈双峰分布。

打开实时脚本

从半正态分布生成非负样本数据集。

rng('default') % For reproducibility
pd = makedist('HalfNormal','mu',0,'sigma',1);
x = random(pd,100,1);

通过使用 'BoundaryCorrection' 名称-值对组参量，使用两种不同的边界校正方法（对数变换和反射）估计 pdf。

pts = linspace(0,5,1000); % points to evaluate the estimator
[f1,xi1] = ksdensity(x,pts,'Support','positive');
[f2,xi2] = ksdensity(x,pts,'Support','positive','BoundaryCorrection','reflection');

绘制两个估计的 pdf。

plot(xi1,f1,xi2,f2)
lgd = legend('log','reflection');
title(lgd, 'Boundary Correction Method')
xl = xlim;
xlim([xl(1)-0.25 xl(2)])

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent log, reflection.

当您指定正支持或有界支持时，ksdensity 使用边界校正方法。默认边界校正方法是对数变换。当 ksdensity 将支持变换回来时，它会在核密度估计器中引入 1/x 项。因此，估计在 x = 0 附近有峰值。另一方面，反射方法不会在边界附近导致不想要的峰值。

打开实时脚本

加载样本数据。 

load hospital

计算并绘制在指定值集处计算的估计 cdf。 

pts = (min(hospital.Weight):2:max(hospital.Weight));
figure()
ecdf(hospital.Weight)
hold on
[f,xi,bw] = ksdensity(hospital.Weight,pts,'Support','positive',...
	'Function','cdf');
plot(xi,f,'-g','LineWidth',2)
legend('empirical cdf','kernel-bw:default','Location','northwest')
xlabel('Patient weights')
ylabel('Estimated cdf')

Figure contains an axes object. The axes object with xlabel Patient weights, ylabel Estimated cdf contains 2 objects of type stair, line. These objects represent empirical cdf, kernel-bw:default.

ksdensity 似乎对累积分布函数估计进行了过度平滑。带宽越小的估计可能产生越接近经验累积分布函数的估计。

返回平滑窗的带宽。 

bw
bw = 
0.1070

使用较小的带宽绘制累积分布函数估计。 

[f,xi] = ksdensity(hospital.Weight,pts,'Support','positive',...
	'Function','cdf','Bandwidth',0.05); 
plot(xi,f,'--r','LineWidth',2)
legend('empirical cdf','kernel-bw:default','kernel-bw:0.05',...
	'Location','northwest')
hold off

Figure contains an axes object. The axes object with xlabel Patient weights, ylabel Estimated cdf contains 3 objects of type stair, line. These objects represent empirical cdf, kernel-bw:default, kernel-bw:0.05.

带宽越小的 ksdensity 估计越匹配经验累积分布函数。

打开实时脚本

加载样本数据。 

load hospital

绘制在 50 个等间距点处计算的估计 cdf。 

figure()
ksdensity(hospital.Weight,'Support','positive','Function','cdf',...
'NumPoints',50)
xlabel('Patient weights')
ylabel('Estimated cdf')

Figure contains an axes object. The axes object with xlabel Patient weights, ylabel Estimated cdf contains an object of type line.

打开实时脚本

从均值为 3 的指数分布生成样本数据。 

rng('default')  % For reproducibility
x = random('exp',3,100,1);

创建一个指示删失的逻辑向量。此处，寿命长于 10 的观测值视为删失。 

T = 10;
cens = (x>T);

计算并绘制估计密度函数。 

figure
ksdensity(x,'Support','positive','Censoring',cens);

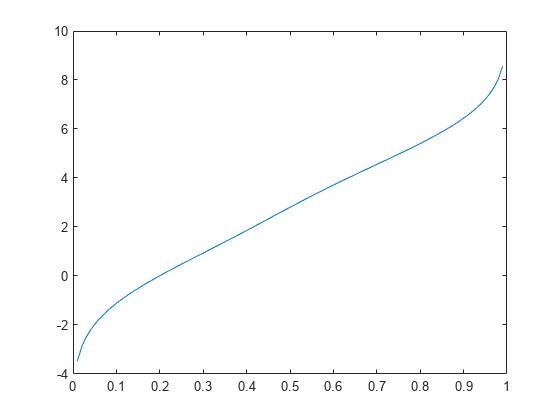
Figure contains an axes object. The axes object contains an object of type line.

计算并绘制生存函数。 

figure
ksdensity(x,'Support','positive','Censoring',cens,...
'Function','survivor');

Figure contains an axes object. The axes object contains an object of type line.

计算并绘制累积风险函数。 

figure
ksdensity(x,'Support','positive','Censoring',cens,...
'Function','cumhazard');

Figure contains an axes object. The axes object contains an object of type line.

打开实时脚本

生成两个正态分布的混合，并在指定的概率值集处绘制估计的逆累积分布函数。 

rng('default')  % For reproducibility
x = [randn(30,1); 5+randn(30,1)];
pi = linspace(.01,.99,99);
figure
ksdensity(x,pi,'Function','icdf');

Figure contains an axes object. The axes object contains an object of type line.

打开实时脚本

生成两个正态分布的混合。 

rng('default')  % For reproducibility
x = [randn(30,1); 5+randn(30,1)];

返回概率密度估计的平滑窗的带宽。 

[f,xi,bw] = ksdensity(x); 
bw
bw = 
1.5141

对于正态密度而言，默认带宽是最优的。

绘制估计密度。 

figure
plot(xi,f);
xlabel('xi')
ylabel('f')
hold on

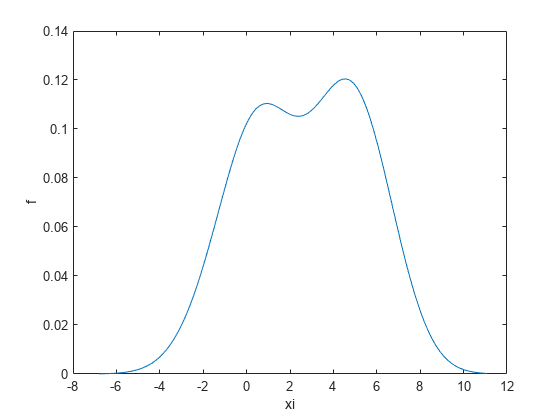
Figure contains an axes object. The axes object with xlabel xi, ylabel f contains an object of type line.

使用增加的带宽值绘制密度。 

[f,xi] = ksdensity(x,'Bandwidth',1.8);
plot(xi,f,'--r','LineWidth',1.5)

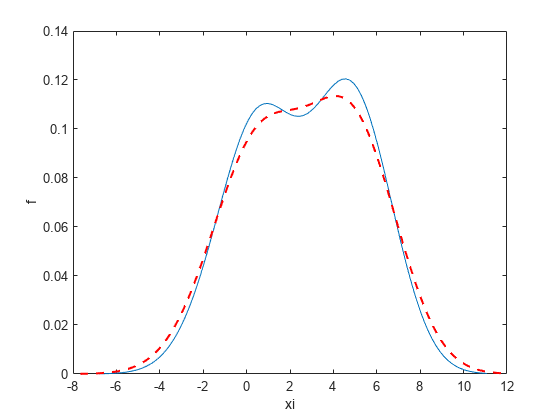
Figure contains an axes object. The axes object with xlabel xi, ylabel f contains 2 objects of type line.

较高的带宽可进一步平滑密度估计，这可能会掩盖分布的某些特征。

现在，使用减小的带宽值绘制密度。 

[f,xi] = ksdensity(x,'Bandwidth',0.8);
plot(xi,f,'-.k','LineWidth',1.5)
legend('bw = default','bw = 1.8','bw = 0.8')
hold off

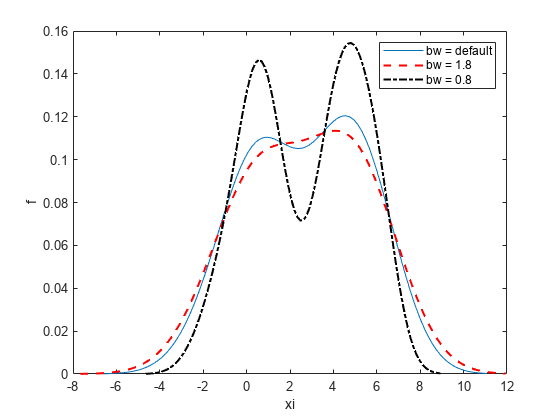
Figure contains an axes object. The axes object with xlabel xi, ylabel f contains 3 objects of type line. These objects represent bw = default, bw = 1.8, bw = 0.8.

带宽越小，对密度估计的平滑程度就越低，这会夸大样本的某些特征。

打开实时脚本

创建一个由点组成的两列向量，在这些点处计算密度。

gridx1 = -0.25:.05:1.25;
gridx2 = 0:.1:15;
[x1,x2] = meshgrid(gridx1, gridx2);
x1 = x1(:);
x2 = x2(:);
xi = [x1 x2];

生成一个 30×2 的矩阵，其中包含来自二元正态分布混合的随机数。

rng('default')  % For reproducibility
x = [0+.5*rand(20,1) 5+2.5*rand(20,1);
            .75+.25*rand(10,1) 8.75+1.25*rand(10,1)];

绘制样本数据的估计密度。

figure
ksdensity(x,xi);

Figure contains an axes object. The axes object contains an object of type surface.

输入参数

全部折叠

ksdensity 返回 f 值的样本数据，指定为列向量或两列矩阵。对一元数据使用列向量，对二元数据使用两列矩阵。

示例: [f,xi] = ksdensity(x)

数据类型: single | double

用于计算 f 的点，指定为向量或两列矩阵。对于一元数据，pts 可以是行向量或列向量。返回的输出 f 的长度等于 pts 中的点数。

示例: pts = (0:1:25); ksdensity(x,pts);

数据类型: single | double

ksdensity 绘图所在图窗的坐标区句柄，指定为句柄。

例如，如果 h 是一个图窗句柄，则 ksdensity 可以绘制到该图窗，如下所示。

示例: ksdensity(h,x)

名称-值参数

全部折叠

将可选参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

如果使用的是 R2021a 之前的版本，请使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: 'Censoring',cens,'Kernel','triangle','NumPoints',20,'Function','cdf' 指定 ksdensity 通过以下方式来估计 cdf：在覆盖数据范围的 20 个等间距点处进行计算，使用三角形核平滑函数，并考虑向量 cens 中的删失数据信息。

核平滑窗的带宽，它是 x 中点数的函数，指定为 "normal-approx" 或 "plug-in"。如果样本数据是二元数据，则 Bandwidth 也可以是二元素向量 [L,U]。

  • 如果 Bandwidth 是 "normal-approx"，ksdensity 会使用正态逼近方法（即西尔弗曼经验法则）来计算带宽。计算的值对于估计正态密度是最优的 [2]，但您可能希望指定更大的值以获得更平滑的结果，或指定更小的值以获得更不平滑的结果。

  • 如果 Bandwidth 是 "plug-in"，ksdensity 会使用 [1] 中所述的改进插件方法来计算带宽。插件方法有时称为谢瑟-琼斯方法。

  • 当 Bandwidth 是正标量时，其值控制概率函数估计的平滑度。随着值增加，概率函数估计变得更平滑。

如果您将 BoundaryCorrection 指定为 "log"（默认值），将 Support 指定为 "positive" 或向量 [L U]，ksdensity 会通过使用对数变换将有界数据转换为无界数据。Bandwidth 的值是基于变换后数据的尺度定义的。

示例: Bandwidth=0.8

数据类型: single | double

边界校正方法，指定为由 'BoundaryCorrection' 和 'log' 或 'reflection' 组成的以逗号分隔的对组。

值描述
'log'

ksdensity 通过以下变换之一将有界数据 x 转换为无界数据。然后，在进行密度估计后，再将其变换回原始有界尺度。

  • 对于一元数据，如果您指定 'Support','positive'，则 ksdensity 应用 log(x)。

  • 对于一元数据，如果您指定 'Support',[L U]，其中 L 和 U 是数值标量且 L < U，则 ksdensity 应用 log((x-L)/(U–x))。

  • 对于二元数据，ksdensity 以与一元数据相同的方式变换 x 的每列。

'Bandwidth' 和 bw 输出的值是基于变换后的值的尺度计算的。

'reflection'

ksdensity 通过在边界附近添加反射数据来增强有界数据，然后返回对应于原始支持的估计值。有关详细信息，请参阅反射方法。

仅当您将 'Support' 指定为非 'unbounded' 值时，ksdensity 才会应用边界校正。

示例: 'BoundaryCorrection','reflection'

指示哪些条目是删失条目的逻辑向量，指定为由 'Censoring' 和一个二值向量组成的以逗号分隔的对组。值 0 表示没有删失，1 表示该观测值有删失。默认为没有删失。此名称-值对组仅对一元数据有效。

示例: 'Censoring',censdata

数据类型: logical

要估计的函数，指定为以逗号分隔的对组，其中包含 'Function' 和以下项之一。

值描述
'pdf'概率密度函数。
'cdf'累积分布函数。
'icdf'

逆累积分布函数。ksdensity 计算 x 中值的估计逆 cdf，并在 pi 中指定的概率值处计算它。

此值仅对一元数据有效。

'survivor'生存函数。
'cumhazard'

累积风险函数。

此值仅对一元数据有效。

示例: 'Function','icdf'

核平滑器的类型，指定为以逗号分隔的对组，其中包含 'Kernel' 和以下项之一。

  • 'normal'（默认值）

  • 'box'

  • 'triangle'

  • 'epanechnikov'

  • 核函数（自定义或内置函数）。将函数指定为函数句柄（例如 @myfunction 或 @normpdf）或指定为字符向量或字符串标量（例如 'myfunction' 或 'normpdf'）。软件使用一个参量调用指定的函数，该参量是数据值与计算密度所在位置之间的距离数组。该函数必须返回相同大小的数组，包含核函数的对应值。

    当 'Function' 为 'pdf' 时，核函数返回密度值。否则，它返回累积概率值。

    当 'Function' 为 'icdf' 时，指定自定义核函数将返回错误。

对于二元数据，ksdensity 对每个维度应用相同的核。

示例: 'Kernel','box'

xi 中等间距点的数量，指定为由 'NumPoints' 和一个标量值组成的以逗号分隔的对组。此名称-值对组仅对一元数据有效。

例如，对于在样本数据范围内 80 个等间距点处的指定函数的核平滑估计，请输入：

示例: 'NumPoints',80

数据类型: single | double

密度支持，指定为以下值之一。

值描述
"unbounded"允许密度可以扩大到整个实数范围（默认值）。
"positive"将密度限制为正值。
"nonnegative"将密度限制为正值和 0。
"negative"将密度限制为负值。
二元素向量 [L U]给出密度支持的有限下界和上界。此选项仅对一元样本数据有效。
2×2 矩阵 [L1 L2; U1 U2]给出密度支持的有限下界和上界。第一行包含下限，第二行包含上限。此选项仅对二元样本数据有效。

对于二元数据，Support 可以指定为 [0 -Inf; Inf Inf] 或 [0 L; Inf U] 的正无界和有界变量的组合。

示例: Support="positive"

示例: Support=[0 10]

数据类型: single | double | char | string

用于创建核密度图的函数，指定为以逗号分隔的对组，其中包含 'PlotFcn' 和以下项之一。

值描述
'surf'使用 surf 创建的三维着色曲面图
'contour'使用 contour 创建的等高线图
'plot3'使用 plot3 创建的三维线图
'surfc'使用 surfc 创建的三维着色曲面图下的等高线图

此名称-值对组仅对二元样本数据有效。

示例: 'PlotFcn','contour'

样本数据的权重，指定为由 'Weights' 和长度为 size(x,1) 的向量组成的以逗号分隔的对组，其中 x 是样本数据。

示例: 'Weights',xw

数据类型: single | double

输出参量

全部折叠

估计函数值，以向量形式返回，向量的长度等于 xi 或 pts 中的点数。

ksdensity 计算 f 时所在的计算点，以向量或两列矩阵形式返回。对于一元数据，默认为 100 个等间距点，这覆盖了 x 中数据的范围。对于二元数据，默认为 900 个等间距点，这些点是使用 meshgrid 从每个维度中的 30 个等间距点创建的。

平滑窗的带宽，以标量值形式返回。

如果您将 'BoundaryCorrection' 指定为 'log'（默认值），将 'Support' 指定为 'positive' 或向量 [L U]，则 ksdensity 通过使用对数变换将有界数据转换为无界数据。bw 的值是基于变换后数据的尺度定义的。

详细信息

全部折叠

替代功能

您也可以使用 MATLAB® kde 函数来估计一元数据的 pdf 或 cdf。与 ksdensity 不同，kde 不支持边界校正方法或数据删失。

参考

[1] Botev, Z. I., J. F. Grotowski, and D. P. Kroese. "Kernel Density Estimation via Diffusion." The Annals of Statistics, vol. 38, no. 5 (October 1, 2010). https://projecteuclid.org/journals/annals-of-statistics/volume-38/issue-5/Kernel-density-estimation-via-diffusion/10.1214/10-AOS799.full

[2] Bowman, A. W., and A. Azzalini. Applied Smoothing Techniques for Data Analysis. New York: Oxford University Press Inc., 1997.

[3] Hill, P. D. “Kernel estimation of a distribution function.” Communications in Statistics - Theory and Methods. Vol 14, Issue. 3, 1985, pp. 605-620.

[4] Jones, M. C. “Simple boundary correction for kernel density estimation.” Statistics and Computing. Vol. 3, Issue 3, 1993, pp. 135-146.

[5] Silverman, B. W. Density Estimation for Statistics and Data Analysis. Chapman & Hall/CRC, 1986.

扩展功能

全部展开

版本历史记录

在 R2006a 之前推出

另请参阅

| |

主题