surfc

曲面图下的等高线图

全页折叠

语法

surfc(X,Y,Z)

surfc(X,Y,Z,C)

surfc(Z)

surfc(Z,C)

surfc(ax,___)

surfc(___,Name,Value)

sc = surfc(___)

说明

surfc(X,Y,Z) 创建一个三维曲面图，其下方有等高线图。曲面图是一个具有实色边和实色面的三维曲面。该函数将矩阵 Z 中的值绘制为由 X 和 Y 定义的 x-y 平面中的网格上方的高度。曲面的颜色根据 Z 指定的高度而变化。

示例

此外，surfc(X,Y,Z,C) 还指定曲面的颜色。

示例

surfc(Z) 创建一个曲面和等高线图，并将 Z 中元素的列索引和行索引分别用作 x 坐标和 y 坐标。

此外，surfc(Z,C) 还指定曲面的颜色。

surfc(ax,___) 将图形绘制到 ax 指定的坐标区中，而不是当前坐标区中。指定坐标区作为第一个输入参量。

surfc(___,Name,Value) 使用一个或多个名称-值对组参量指定曲面属性。例如，'FaceAlpha',0.5 创建半透明曲面。

示例

sc = surfc(___) 返回包含图曲面对象和等高线对象的图形数组。使用 sc 修改所创建的曲面图和等高线图。有关属性列表，请参阅 Surface 属性和 Contour 属性。

示例

全部折叠

显示曲面图下的等高线图

打开实时脚本

创建三个相同大小的矩阵。然后将它们绘制为曲面，并在曲面图下显示等高线图。曲面的高度和颜色均使用 Z 确定。

[X,Y] = meshgrid(1:0.5:10,1:20);
Z = sin(X) + cos(Y);
surfc(X,Y,Z)

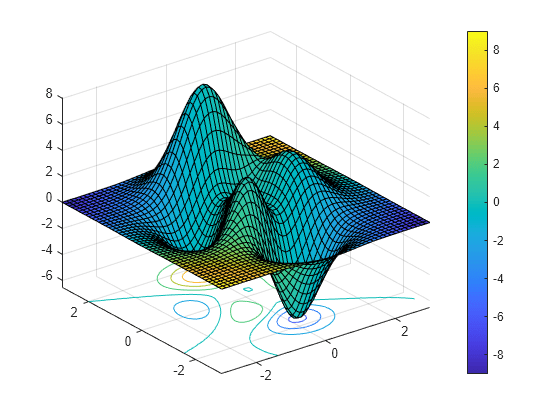
Figure contains an axes object. The axes object contains 2 objects of type surface, contour.

指定曲面和等高线图的颜色图颜色

打开实时脚本

通过采用第四个矩阵输入 C 来指定曲面和等高线图的颜色。曲面图使用 Z 表示高度，C 表示颜色。使用颜色图指定颜色，该颜色图使用单个数字表示色谱上的颜色。使用颜色图时，C 与 Z 大小相同。向图中添加颜色栏以显示 C 中的数据值如何对应于颜色图中的颜色。

[X,Y] = meshgrid(-3:.125:3);
Z = peaks(X,Y);
C = X.*Y;
surfc(X,Y,Z,C)
colorbar

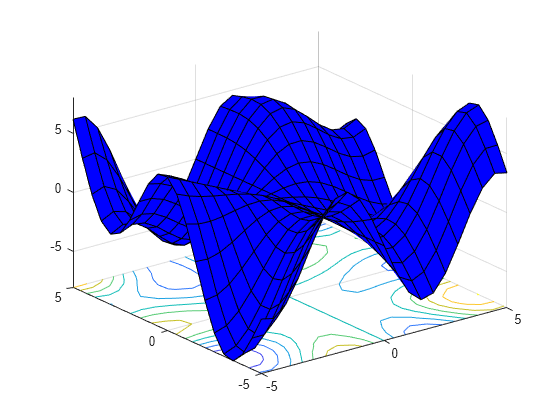
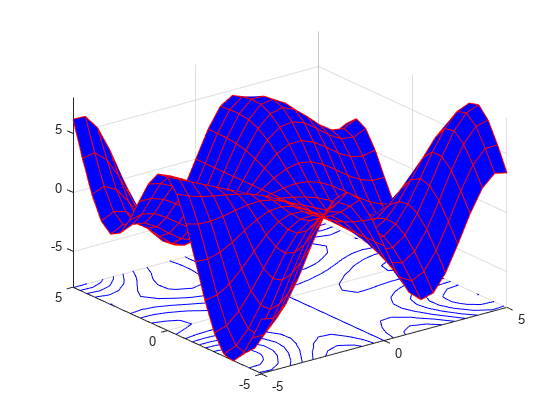
Figure contains an axes object. The axes object contains 2 objects of type surface, contour.

修改曲面图和等高线图的外观

打开实时脚本

通过将 FaceColor 名称-值对组的值指定为 'b'，创建一个蓝色曲面图，其下方有等高线图。要允许进一步修改，请将包含曲面和等高线对象的图形数组赋给变量 sc。

[X,Y] = meshgrid(-5:.5:5);
Z = Y.*sin(X) - X.*cos(Y);
sc = surfc(X,Y,Z,'FaceColor','b');

Figure contains an axes object. The axes object contains 2 objects of type surface, contour.

对 sc 进行索引，以访问和修改所创建的曲面和等高线图的属性。可通过 sc(1) 访问曲面图，通过 sc(2) 访问等高线图。例如，通过设置 EdgeColor 属性来更改两个绘图的边颜色。

sc(1).EdgeColor = 'r';
sc(2).EdgeColor = 'b';

Figure contains an axes object. The axes object contains 2 objects of type surface, contour.

更改等高线的位置

打开实时脚本

默认情况下，等高线显示在最小 z 层级，但您可以通过设置 ZLocation 属性来更改其位置。

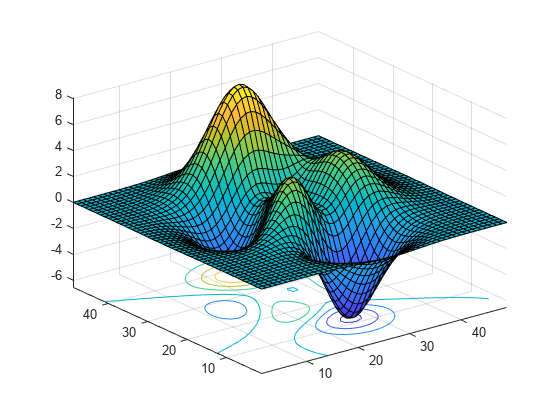
将 peaks 数据集显示为曲面图，等高线位于最小 z 层级。当您调用 surfc 函数时，请指定返回参量，以便您 Contour 对象。

Z = peaks;
sc = surfc(Z);

Figure contains an axes object. The axes object contains 2 objects of type surface, contour.

获取当前坐标区，并将 z 轴的上限扩展到 15。然后将等高线移至最大 z 层级。

ax = gca;
ax.ZLim(2) = 15;
sc(2).ZLocation = 'zmax';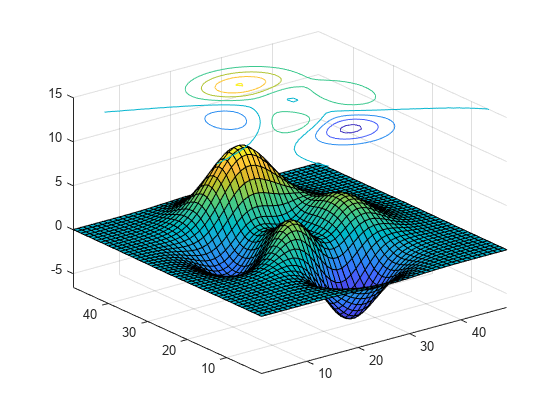

Figure contains an axes object. The axes object contains 2 objects of type surface, contour.

输入参数

全部折叠

`X` — x 坐标
矩阵 | 向量

x 坐标，指定为大小与 Z 相同的矩阵或长度为 n 的向量，其中 [m,n] = size(Z)。如果未指定 X 和 Y 的值，surfc 将使用向量 (1:n) 和 (1:m)。

当 X 是矩阵时，这些值必须在一个维度上严格递增或递减，而在另一个维度上保持不变。这个变化的维度必须与在 Y 中变化的维度相反。您可以使用 meshgrid 函数创建 X 和 Y 矩阵。

当 X 是向量时，值必须严格递增或递减。

曲面和等高线对象的 XData 属性存储 x 坐标。

示例: X = 1:10

示例: X = [1 2 3; 1 2 3; 1 2 3]

示例: [X,Y] = meshgrid(-5:0.5:5)

`Y` — y 坐标
矩阵 | 向量

y 坐标，指定为大小与 Z 相同的矩阵或长度为 m 的向量，其中 [m,n] = size(Z)。如果未指定 X 和 Y 的值，surfc 将使用向量 (1:n) 和 (1:m)。

当 Y 是矩阵时，这些值必须在一个维度上严格递增或递减，而在另一个维度上保持不变。这个变化的维度必须与在 X 中变化的维度相反。您可以使用 meshgrid 函数创建 X 和 Y 矩阵。

当 Y 是向量时，值必须严格递增或递减。

曲面和等高线对象的 YData 属性存储 y 坐标。

示例: Y = 1:10

示例: Y = [1 1 1; 2 2 2; 3 3 3]

示例: [X,Y] = meshgrid(-5:0.5:5)

`Z` — z 坐标
矩阵

z 坐标，指定为矩阵。Z 必须有至少两行两列。

Z 指定在每个 x-y 坐标处的曲面图高度。如果未指定颜色，则 Z 还用于指定曲面颜色。

曲面和等高线对象的 ZData 属性存储 z 坐标。

示例: Z = [1 2 3; 4 5 6]

示例: Z = sin(x) + cos(y)

`C` — 颜色数组
矩阵 | RGB 三元组的 `m`×`n`×`3` 数组

颜色数组，指定为由颜色图索引组成的 m×n 矩阵或 RGB 三元组的 m×n×3 数组，其中 Z 为 m×n。

要使用颜色图颜色，请将 C 指定为矩阵。对于曲面上的每个网格点，C 指示颜色图中的一种颜色。曲面对象的 CDataMapping 属性控制 C 中的值如何对应颜色图中的颜色。
要使用真彩色，请将 C 指定为 RGB 三元组数组。

有关详细信息，请参阅颜色图和真彩色之间的差异。

曲面对象的 CData 属性存储颜色数组。如果要对曲面着色进行更多控制，请使用 FaceColor 和 EdgeColor 属性。

`ax` — 绘图所用的坐标区
坐标区对象

要在其中绘图的坐标区，指定为 axes 对象。如果未指定坐标区，则 surfc 在当前坐标区中绘图。

名称-值参数

全部折叠

以 Name1=Value1,...,NameN=ValueN 的形式指定可选参量对组，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: surfc(X,Y,Z,'FaceAlpha',0.5,'EdgeColor','none') 创建一个半透明曲面，并且不绘制边缘。

注意

此处所列的属性只是一部分。有关完整列表，请参阅 Surface 属性。

`EdgeColor` — 边缘线条颜色
`'none'` | `'flat'` | `'interp'` | RGB 三元组 | 十六进制颜色代码 | `'r'` | `'g'` | `'b'` | ...

边线颜色，指定为下面列出的值之一。默认颜色 [0 0 0] 对应于黑边。

值	描述
`'none'`	不绘制边。
`'flat'`	根据 `CData` 属性中的值，对每个边使用不同的颜色。首先您必须将 `CData` 属性指定为矩阵，大小与 `ZData` 相同。每个面（正的 x 和 y 方向）的第一个顶点处的颜色值确定相邻边的颜色。当 `EdgeAlpha` 属性设置为 `'interp'` 时，不能使用此值。
`'interp'`	根据 `CData` 属性中的值，对每个边使用插补着色。首先您必须将 `CData` 属性指定为矩阵，大小与 `ZData` 相同。通过基于各顶点处颜色值进行线性插值，每条边上的颜色会渐变。当 `EdgeAlpha` 属性设置为 `'flat'` 时，不能使用此值。
RGB 三元组、十六进制颜色代码或颜色名称	对所有边使用指定的颜色。此选项不会使用 `CData` 属性中的颜色值。

RGB 三元组和十六进制颜色代码对于指定自定义颜色非常有用。

RGB 三元组是包含三个元素的行向量，其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于 [0,1] 范围内，例如 [0.4 0.6 0.7]。
十六进制颜色代码是字符向量或字符串标量，以井号 (#) 开头，后跟三个或六个十六进制数字，范围可以是 0 到 F。这些值不区分大小写。因此，颜色代码 "#FF8800" 与 "#ff8800"、"#F80" 与 "#f80" 是等效的。

此外，还可以按名称指定一些常见的颜色。下表列出了命名颜色选项、等效 RGB 三元组和十六进制颜色代码。

颜色名称	短名称	RGB 三元组	十六进制颜色代码
`"red"`	`"r"`	`[1 0 0]`	`"#FF0000"`
`"green"`	`"g"`	`[0 1 0]`	`"#00FF00"`
`"blue"`	`"b"`	`[0 0 1]`	`"#0000FF"`
`"cyan"`	`"c"`	`[0 1 1]`	`"#00FFFF"`
`"magenta"`	`"m"`	`[1 0 1]`	`"#FF00FF"`
`"yellow"`	`"y"`	`[1 1 0]`	`"#FFFF00"`
`"black"`	`"k"`	`[0 0 0]`	`"#000000"`
`"white"`	`"w"`	`[1 1 1]`	`"#FFFFFF"`

下表列出了浅色和深色主题中绘图的默认调色板。

调色板调色板颜色

调色板	调色板颜色
`"gem"` - 浅色主题默认值在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。
`"glow"` - 深色主题默认值

"gem" - 浅色主题默认值

在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。

Sample of the "gem" color palette

"glow" - 深色主题默认值

Sample of the "glow" color palette

您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如，获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。

RGB = orderedcolors("gem");
H = rgb2hex(RGB);

在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。

在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。

`LineStyle` — 线型
`"-"` (默认) | `"--"` | `":"` | `"-."` | `"none"`

线型，指定为下表中列出的选项之一。

线型	描述	表示的线条
`"-"`	实线
`"--"`	虚线
`":"`	点线
`"-."`	点划线
`"none"`	无线条	无线条

`FaceColor` — 面颜色
`'flat'` (默认) | `'interp'` | `'none'` | `'texturemap'` | RGB 三元组 | 十六进制颜色代码 | `'r'` | `'g'` | `'b'` | ...

面颜色，指定为下表中的值之一。

值	描述
`'flat'`	根据 `CData` 属性中的值，对每个面使用不同的颜色。首先您必须将 `CData` 属性指定为矩阵，大小与 `ZData` 相同。每个面的第一个顶点（正 x 和 y 方向）的颜色值决定整个面的颜色。当 `FaceAlpha` 属性设置为 `'interp'` 时，不能使用此值。
`'interp'`	根据 `CData` 属性中的值，对每个面使用插补着色。首先您必须将 `CData` 属性指定为矩阵，大小与 `ZData` 相同。通过基于各顶点处颜色值进行插值，每个面上的颜色会渐变。当 `FaceAlpha` 属性设置为 `'flat'` 时，不能使用此值。
RGB 三元组、十六进制颜色代码或颜色名称	对所有面使用指定的颜色。此选项不会使用 `CData` 属性中的颜色值。
`'texturemap'`	变换 `CData` 中的颜色数据，以便其符合曲面。
`'none'`	不绘制面。

RGB 三元组和十六进制颜色代码对于指定自定义颜色非常有用。

RGB 三元组是包含三个元素的行向量，其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于 [0,1] 范围内，例如 [0.4 0.6 0.7]。
十六进制颜色代码是字符向量或字符串标量，以井号 (#) 开头，后跟三个或六个十六进制数字，范围可以是 0 到 F。这些值不区分大小写。因此，颜色代码 "#FF8800" 与 "#ff8800"、"#F80" 与 "#f80" 是等效的。

此外，还可以按名称指定一些常见的颜色。下表列出了命名颜色选项、等效 RGB 三元组和十六进制颜色代码。

颜色名称	短名称	RGB 三元组	十六进制颜色代码
`"red"`	`"r"`	`[1 0 0]`	`"#FF0000"`
`"green"`	`"g"`	`[0 1 0]`	`"#00FF00"`
`"blue"`	`"b"`	`[0 0 1]`	`"#0000FF"`
`"cyan"`	`"c"`	`[0 1 1]`	`"#00FFFF"`
`"magenta"`	`"m"`	`[1 0 1]`	`"#FF00FF"`
`"yellow"`	`"y"`	`[1 1 0]`	`"#FFFF00"`
`"black"`	`"k"`	`[0 0 0]`	`"#000000"`
`"white"`	`"w"`	`[1 1 1]`	`"#FFFFFF"`

下表列出了浅色和深色主题中绘图的默认调色板。

调色板调色板颜色

调色板	调色板颜色
`"gem"` - 浅色主题默认值在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。
`"glow"` - 深色主题默认值

"gem" - 浅色主题默认值

在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。

Sample of the "gem" color palette

"glow" - 深色主题默认值

Sample of the "glow" color palette

RGB = orderedcolors("gem");
H = rgb2hex(RGB);

在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。

在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。

`FaceAlpha` — 面透明度
1 (默认) | 范围 `[0,1]` 中的标量 | `'flat'` | `'interp'` | `'texturemap'`

面透明度，指定为下列值之一：

范围 [0,1] 中的标量 - 在所有面上使用统一的透明度。值为 1 时完全不透明，值为 0 时完全透明。介于 0 和 1 之间的值表示半透明。此选项不会使用 AlphaData 属性中的透明度值。
'flat' - 根据 AlphaData 属性中的值，对每个面使用不同的透明度。第一个顶点的透明度值确定整个面的透明度。首先您必须将 AlphaData 属性指定为矩阵，大小与 ZData 属性相同。FaceColor 属性也必须设置为 'flat'。
'interp' - 根据 AlphaData 属性中的值，对每个面使用插值透明度。通过基于各顶点处透明度数值进行插值，每个面上的透明度会渐变。首先您必须将 AlphaData 属性指定为矩阵，大小与 ZData 属性相同。FaceColor 属性也必须设置为 'interp'。
'texturemap' - 变换 AlphaData 中的数据，以便其符合曲面。

`FaceLighting` — 光源对象对面的影响
`'flat'` | `'gouraud'` | `'none'`

光源对象对面的影响，指定为下列值之一：

'flat' - 将光源均匀地应用于每个面上。使用此值可查看分面着色对象。
'gouraud' - 改变各个面的光源。计算顶点处的光照，然后以在各个面中进行光照插值。使用此值可查看曲面。
'none' - 不将来自光源对象的光源应用于各个面。

要向坐标区中添加光对象，请使用 light 函数。

注意

'phong' 值已被删除。请改用 'gouraud'。

扩展功能

全部展开

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

surfc 函数支持 GPU 数组输入，但有以下用法说明和限制：

此函数接受 GPU 数组，但不在 GPU 上运行。

有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

用法说明和限制：

此函数在分布式数组上运行，但在客户端 MATLAB^® 中执行。

有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

另请参阅

函数

meshc | surf | meshgrid | imagesc | view | shading | pcolor | colormap | contour

属性

Surface 属性 | Contour 属性

surfc

语法

说明

示例

显示曲面图下的等高线图

指定曲面和等高线图的颜色图颜色

修改曲面图和等高线图的外观

更改等高线的位置

输入参数

X — x 坐标 矩阵 | 向量

Y — y 坐标 矩阵 | 向量

Z — z 坐标 矩阵

C — 颜色数组 矩阵 | RGB 三元组的 m×n×3 数组

ax — 绘图所用的坐标区 坐标区对象

名称-值参数

EdgeColor — 边缘线条颜色 'none' | 'flat' | 'interp' | RGB 三元组 | 十六进制颜色代码 | 'r' | 'g' | 'b' | ...

LineStyle — 线型 "-" (默认) | "--" | ":" | "-." | "none"

FaceColor — 面颜色 'flat' (默认) | 'interp' | 'none' | 'texturemap' | RGB 三元组 | 十六进制颜色代码 | 'r' | 'g' | 'b' | ...

FaceAlpha — 面透明度 1 (默认) | 范围 [0,1] 中的标量 | 'flat' | 'interp' | 'texturemap'

FaceLighting — 光源对象对面的影响 'flat' | 'gouraud' | 'none'

扩展功能

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

另请参阅

函数

属性

主题

`X` — x 坐标
矩阵 | 向量

`Y` — y 坐标
矩阵 | 向量

`Z` — z 坐标
矩阵

`C` — 颜色数组
矩阵 | RGB 三元组的 `m`×`n`×`3` 数组

`ax` — 绘图所用的坐标区
坐标区对象

`EdgeColor` — 边缘线条颜色
`'none'` | `'flat'` | `'interp'` | RGB 三元组 | 十六进制颜色代码 | `'r'` | `'g'` | `'b'` | ...

`LineStyle` — 线型
`"-"` (默认) | `"--"` | `":"` | `"-."` | `"none"`

`FaceColor` — 面颜色
`'flat'` (默认) | `'interp'` | `'none'` | `'texturemap'` | RGB 三元组 | 十六进制颜色代码 | `'r'` | `'g'` | `'b'` | ...

`FaceAlpha` — 面透明度
1 (默认) | 范围 `[0,1]` 中的标量 | `'flat'` | `'interp'` | `'texturemap'`

`FaceLighting` — 光源对象对面的影响
`'flat'` | `'gouraud'` | `'none'`

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。