将数据表示为曲面

用来绘制数据网格的函数

MATLAB^® 图形通过 x-y 平面中的矩形网格上方的点的 z 坐标来定义曲面。通过用直线连接相邻点来形成绘图。曲面图可用于可视化因太大而无法以数字形式显示的矩阵，还可用于绘制包含两个变量的函数。

MATLAB 可以创建不同形式的曲面图。网格图是指仅对连接定义点的线条进行着色的线框曲面图。曲面图对连接线和面都进行着色。下表列出了曲面图的各种形式。

函数	用于创建
`mesh`、`surf`	曲面图
`meshc`、`surfc`	下方带有等高线图的曲面图
`meshz`	带帷幕图（参考平面）的曲面图
`pcolor`	单一着色平面图（值仅与颜色成比例）
`surfl`	从指定方向照亮的曲面图
`surface`	用于创建曲面图形对象的低级函数（高级函数的基础）

用于对数据进行网格化和插值的函数

当您需要对数据进行重构和插值以便将它们表示为曲面时，这些函数很有用。

函数	用于创建
`meshgrid`	二维和三维空间中的矩形网格
`griddata`	散点数据插值
`griddedInterpolant`	网格数据插值
`scatteredInterpolant`	散点数据插值

有关如何对数据进行插值的讨论，请参阅插入网格数据和内插散点数据。

网格图和曲面图

mesh 和 surf 命令可创建矩阵数据的三维曲面图。如果 Z 是矩阵，其元素 Z(i,j) 定义曲面在基础 (i,j) 网格的上方的高度，则

mesh(Z)

生成曲面的彩色线框视图并在三维视图中显示。类似地，

surf(Z)

生成曲面的着色分面视图并在三维视图中显示。通常这些分面为四边形，每个分面为一种固定颜色，边为黑色网格线，但使用 shading 命令可以消除网格线 (shading flat) 或选择对整个分面进行插补着色 (shading interp)。

曲面对象属性用于进一步控制曲面的视觉外观。您可以指定边的线型、顶点标记、面的颜色以及光照特性等。

可视化包含两个变量的函数

要显示包含两个变量的函数 z = f(x,y)，需要生成 X 和 Y 矩阵，它们分别由函数域内重复的行和列组成。您将使用这两个矩阵来计算和绘制该函数。
meshgrid 函数将 x 和 y 两个向量指定的域转换为矩阵 X 和 Y。然后，您可以使用这两个矩阵来计算包含两个变量的函数：X 的行是向量 x 的副本，Y 的列是向量 y 的副本。

例 1. 示例：说明 meshgrid 的用法

下面以 sin(r)/r（即 sinc 函数）为例说明 meshgrid 的用法。要计算此函数在 x 和 y 都为 -8 到 8 之间时的值，只需向 meshgrid 传递一个向量参数，此参数将用于完成两个方向上的计算。

[X,Y] = meshgrid(-8:.5:8);
R = sqrt(X.^2 + Y.^2) + eps;

矩阵 R 包含到矩阵中心（即原点）之间的距离。加上 eps 是为了防止被零除（下一步），否则将在数据中生成 Inf 值。

构造 sinc 函数并使用 mesh 绘制 Z 值将生成一个三维曲面。

Z = sin(R)./R;
figure
mesh(X,Y,Z)

隐线消除

默认情况下，MATLAB 会消除网格图中不可见的隐线，即使网格图的面未填充也是如此。您可以使用 hidden 命令禁用隐线消除并使网格图的面透明：

hidden off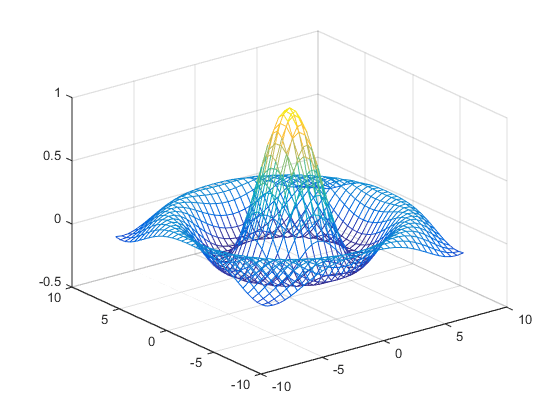

渲染曲面形状

MATLAB 提供了许多方法来增强图形所含信息的显示。例如，下面这个 sinc 函数图使用的数据与上一个图相同，但它利用光照、视图调整和不同的颜色图来渲染所绘制函数（daspect、axis、view 和 camlight）的形状。

figure
colormap hsv
surf(X,Y,Z,'FaceColor','interp',...
   'EdgeColor','none',...
   'FaceLighting','gouraud')
daspect([5 5 1])
axis tight
view(-50,30)
camlight left

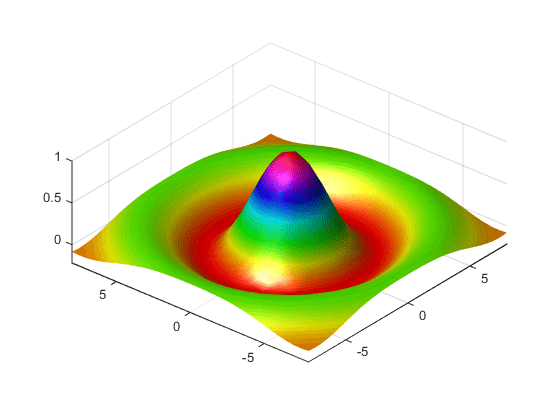
有关曲面图的详细信息，请参阅 surf 函数。

非均匀采样数据的曲面图

您可以使用 meshgrid 创建要用于计算和绘制 sinc 函数的均匀采样数据点的网格。然后，MATLAB 通过连接相邻矩阵元素来形成四边形网格，从而生成曲面图。

要根据非均匀采样数据生成曲面图，请使用 scatteredInterpolant 在等间距处进行插值，然后按常规方式使用 mesh 和 surf。

示例 - 在曲面上显示非均匀数据

此示例计算 sinc 函数在特定范围内随机点处的值，然后生成均匀采样的数据以显示为曲面图。此过程涉及以下任务：

使用 linspace 在非均匀采样的数据范围内生成等间距值。
使用 meshgrid 并利用 linspace 的输出生成绘图网格。
使用 scatteredInterpolant 将按 meshgrid 返回的等间距网格对非固定间隔采样数据进行插值。
使用绘图函数显示数据。

在 [-8, 8] 范围内生成非均匀采样的数据，并利用它来计算函数：

x = rand(100,1)*16 - 8;
y = rand(100,1)*16 - 8;
r = sqrt(x.^2 + y.^2) + eps;
z = sin(r)./r;

linspace 函数为创建具有所需元素数的等间距数据提供了一种便捷的方式。下面的语句在随机数据范围内生成向量，分辨率与前面的 sinc 示例中 -8:.5:8 语句生成的分辨率相同：
```
xlin = linspace(min(x),max(x),33);
ylin = linspace(min(y),max(y),33);
```
现在使用这些点生成等间距网格：
```
[X,Y] = meshgrid(xlin,ylin);
```
此过程的关键是基于函数在原始数据点的值（本例中为随机数据点），使用 scatteredInterpolant 在等间距点处进行函数值插值。此语句使用默认的线性插值生成新数据：
```
f = scatteredInterpolant(x,y,z);
Z = f(X,Y);
```

绘制插值和非均匀数据以生成：

figure
mesh(X,Y,Z) %interpolated
axis tight; hold on
plot3(x,y,z,'.','MarkerSize',15) %nonuniform

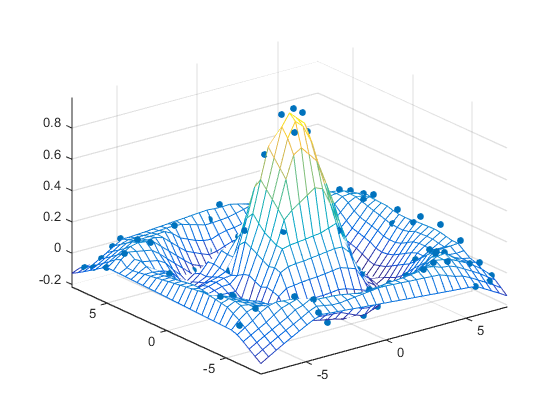
重构数据

假设您有一个数据集，其中包含以下 (X, Y, Z) 三元组：

X	Y	Z
1	1	152
2	1	89
3	1	100
4	1	100
5	1	100
1	2	103
2	2	0
3	2	100
4	2	100
5	2	100
1	3	89
2	3	13
3	3	100
4	3	100
5	3	100
1	4	115
2	4	100
3	4	187
4	4	200
5	4	111
1	5	100
2	5	85
3	5	111
4	5	97
5	5	48

您可以先通过调整数据结构，使用各种 MATLAB 图形函数（如 surf、contour 和 stem3）来表示这些向量形式的数据。使用 (X, Y) 值定义 x-y 平面上存在 Z 值的点处的坐标。reshape 和 transpose 函数可以调整数据结构，使 (X, Y, Z) 三元组形成矩形网格：

x = reshape(X,5,5)';
y = reshape(Y,5,5)';
z = reshape(Z,5,5)';

重构会产生三个 5×5 数组：

x =

     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5
     1     2     3     4     5

y =

     1     1     1     1     1
     2     2     2     2     2
     3     3     3     3     3
     4     4     4     4     4
     5     5     5     5     5

z =

   152    89   100   100   100
   103     0   100   100   100
    89    13   100   100   100
   115   100   187   200   111
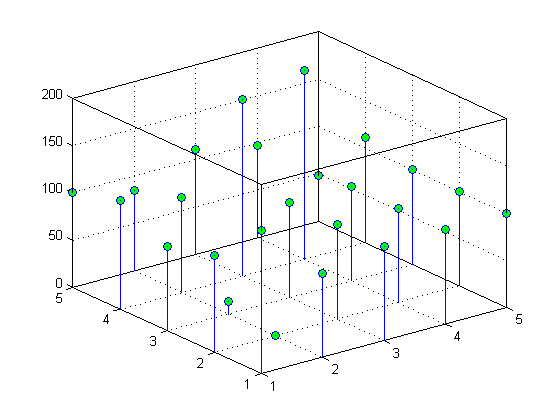
   100    85   111    97    48

现在您可以相对于 X 和 Y 来表示 Z 的值。例如，创建一个三维针状图：

stem3(x,y,z,'MarkerFaceColor','g')

参数化曲面

用来绘制曲面的函数可以使用两个额外的向量或矩阵参数来表示具有特定 x 和 y 数据的曲面。如果 Z 是 m×n 矩阵，其中 x 是 n 向量，y 是 m 向量，则

mesh(x,y,Z,C)

表示顶点颜色为 C(i,j) 并位于以下点的网格曲面

(x(j), y(i), Z(i,j))

其中 x 对应于 Z 的各列，y 对应于各行。

更常见的是，如果 X、Y、Z 和 C 是维度相同的矩阵，则

mesh(X,Y,Z,C)

表示顶点颜色为 C(i,j) 并位于以下点的网格曲面

(X(i,j), Y(i,j), Z(i,j))

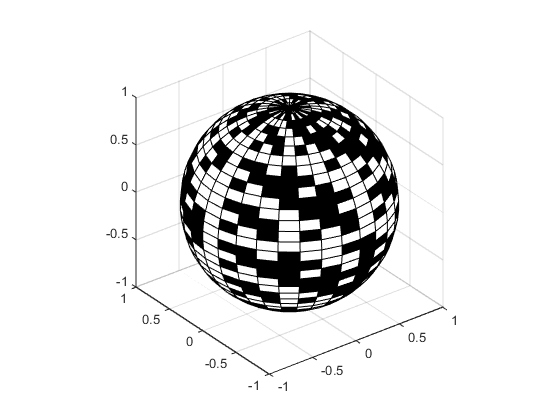
此示例使用球面坐标来绘制球体，并使用 Hadamard 矩阵（信号处理编码理论中使用的一种正交矩阵）中的加号和减号图案进行着色。向量 theta 和 phi 的范围分别为 -π ≤ theta ≤ π 和 -π/2 ≤ phi ≤ π/2。由于 theta 是行向量而 phi 是列向量，因此产生矩阵 X、Y 和 Z 的乘法是向量外积。

figure
k = 5;
n = 2^k-1;
theta = pi*(-n:2:n)/n;
phi = (pi/2)*(-n:2:n)'/n;
X = cos(phi)*cos(theta);
Y = cos(phi)*sin(theta);
Z = sin(phi)*ones(size(theta));
colormap([0 0 0;1 1 1])
C = hadamard(2^k); 
surf(X,Y,Z,C)
axis square