网格数据插值
网格数据由形成网格的等间距点上的值或测量值组成。网格数据应用于许多领域,如气象学、测绘学和医学成像。在这些领域,经常以固定空间间隔取测量值,且可能随时间进行测量。这些有序的数据网格的范围可以从一维(对于简单时间序列)到四维(对于随时间变化的三维体测量)或更高维。网格数据的一些示例有:
一维:随时间变化的股票价格
二维:曲面的温度
三维:大脑的 MRI 图像
四维:随时间变化的海洋水体测量值
在所有这些应用中,基于网格的插值可高效地将数据扩充到未进行测量的点。例如,如果您有某股票的小时价格数据,可以使用插值来逼近每 15 分钟的价格。
MATLAB 网格插值函数
MATLAB® 提供几种用于基于网格插值的工具:
网格创建函数
meshgrid 和 ndgrid 函数创建各种维度的网格。meshgrid 可以创建二维或三维网格,而 ndgrid 可以创建任意维数的网格。这些函数使用不同输出格式返回网格。您可以使用 pagetranspose(从 R2020b 开始)或 permute 函数在这些网格格式之间进行转换,以交换网格的前两个维度。
插值函数:
interp 系列函数包括 interp1、interp2、interp3 和 interpn。每个函数都设计用于对具有特定维数的数据进行插值。interp2 和 interp3 使用 meshgrid 格式的网格,而 interpn 使用 ndgrid 格式的网格。
插值对象
griddedInterpolant 对象支持对 ndgrid 格式的数据进行任意维数的插值。这些对象还支持多值插值(从 R2021a 开始),其中每个网格点可以有多个关联的值。
与使用 interp 函数相比,使用 griddedInterpolant 对象具有内存和性能优势。griddedInterpolant 为插值对象的重复查询提供了显著的性能改进,而 interp 函数在每次调用时都会执行新计算。此外,griddedInterpolant 以内存高效格式存储采样点(作为简洁网格),并以多线程方式利用多核计算机处理器。
网格表示法
MATLAB 允许按以下三种方式之一表示网格:完整网格、简洁网格或默认网格。默认网格和简洁网格主要是分别为了方便使用和提高效率。
完整网格
完整网格是一种以显式方式定义所有点的网格。ndgrid 和 meshgrid 的输出定义一个完整网格。您可以创建均匀的完整网格,其中每个维度中的点具有相等的间距,或创建非均匀的完整网格,其中一个或多个维度的间距不同。均匀网格在不同维度上可以有不同间距,但每个维度内的间距是固定的。
| 均匀 | 均匀 | 非均匀 |
|---|---|---|
|
|
|
均匀完整网格的示例如下:
[X,Y] = meshgrid([1 2 3],[3 6 9 12])
X =
1 2 3
1 2 3
1 2 3
1 2 3
Y =
3 3 3
6 6 6
9 9 9
12 12 12简洁网格
在处理大型网格时,显式定义网格中的每个点会消耗大量内存。简洁网格表示法无需完整网格的内存使用量。简洁网格表示法只存储网格向量(每个维度对应一个),而不存储整个网格。各网格向量共同隐式定义了网格。事实上,meshgrid 和 ndgrid 的输入是网格向量,这些函数复制网格向量以形成完整网格。简洁网格表示法使您能够绕过网格创建,并将网格向量直接提供给插值函数。
例如,假设有两个向量,x1 = 1:3 和 x2 = 1:5。可以将这些向量视为沿 x1 方向的一组坐标和沿 x2 方向的一组坐标,如下所示:
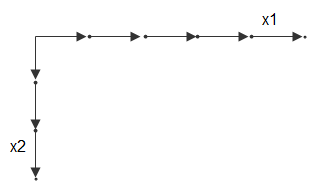
每个箭头指向一个位置。使用这两个向量可以定义一组网格点,其中一组坐标由 x1 给定,另一组坐标由 x2 给定。在复制网格向量时,它们构成了组成完整网格的两个坐标数组:
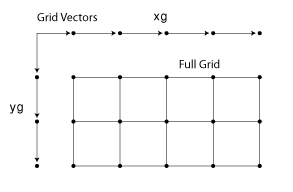
您的输入网格向量可能是单调或非单调的。单调向量所含的值在该维中递增,或在该维中递减。反之,非单调向量含有的值会上下波动。如果输入网格向量是非单调的,如 [2 4 6 3 1],则 [X1,X2] = ndgrid([2 4 6 3 1]) 输出非单调网格。如果要将网格传递给其他 MATLAB 函数,网格向量应当是单调的。sort 函数可用于确保单调性。
默认网格
在某些应用中,只有网格点的值才是重要的,而网格点之间的距离并不重要。例如,大多数 MRI 扫描收集的数据在所有方向上都是等间距的。在这种情况下,您可以允许插值函数自动生成默认网格表示来处理数据。为此,无需提供插值函数的网格输入。当您不提供网格输入时,该函数会自动将数据视为位于单位间距的网格上。该函数在执行时创建此单位间距的网格,省去您自己创建网格的麻烦。
示例:二维网格上的温度插值
假设在一个曲面上以 5 厘米固定间隔收集温度数据,在每个方向上延伸 20 厘米。使用 meshgrid 创建完整网格。
[X,Y] = meshgrid(0:5:20)
X =
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
Y =
0 0 0 0 0
5 5 5 5 5
10 10 10 10 10
15 15 15 15 15
20 20 20 20 20每个网格点的坐标 (x,y) 表示为 X 和 Y 矩阵中的对应元素。第一个网格点由 [X(1) Y(1)] 给出,即 [0 0],下一个网格点由 [X(2) Y(2)] 给出,即 [0 5],依此类推。
现在,创建一个矩阵来表示网格上的温度测量值,然后将数据绘制为曲面。
T = [1 1 10 1 1;
1 10 10 10 10;
100 100 1000 100 100;
10 10 10 10 1;
1 1 10 1 1];
surf(X,Y,T)
view(2)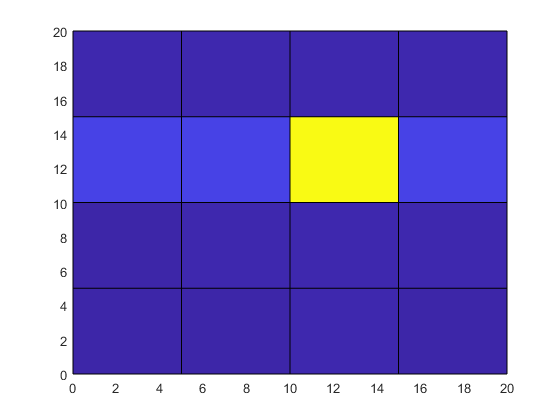
虽然中心网格点的温度很高,但从原始数据来看,其位置和对周围网格点的影响并不明显。
要将数据分辨率提高 10 倍,请使用 interp2 将温度数据插值到使用 0.5 厘米间隔的更精细的网格上。再次使用 meshgrid 创建由矩阵 Xq 和 Yq 表示的更精细的网格。然后,将 interp2 与原始网格、温度数据和新网格点结合使用,绘制生成的数据。默认情况下,interp2 在每个维度中使用线性插值。
[Xq,Yq] = meshgrid(0:0.5:20); Tq = interp2(X,Y,T,Xq,Yq); surf(Xq,Yq,Tq) view(2)
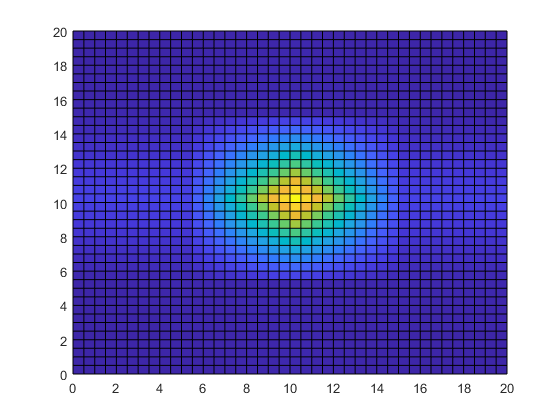
对温度数据进行插值可以增加图像的细节,并大大提高测量区域内数据的有用性。
网格插值方法
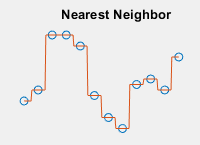
MATLAB 中基于网格的插值函数和对象提供几种不同插值方法。在选择插值方法时,切记有些方法比其他方法需要更多的内存或更长的计算时间。您需要权衡这些资源,以实现结果所需要的平滑度。下表给出了应用于同一一维数据的每种插值方法的预览,并概述了每种方法的优点、取舍和要求。
| 方法 | 描述 |
|---|---|
|
| 查询点处的插入值是距采样网格点最近的值。
|
|
| 查询点处的插入值是下一个采样网格点的值。
|
|
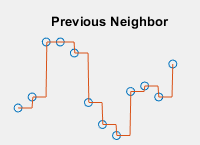
| 查询点处的插入值是上一个采样网格点的值。
|
|
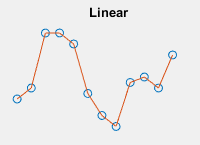
| 查询点处的插入值基于各维中邻近网格点处数值的线性插值。
|
|
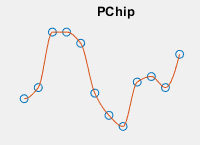
| 查询点处的插入值基于邻近网格点处数值的保形分段三次插值。
|
|
| 查询点处的插入值基于各维中邻近网格点处数值的三次插值。
|
|
| 查询点处的插入值使用次数最大为 3 的分段多项式函数基于各维中邻近网格点的值进行计算而得。为防过冲,已修正 Akima 公式。
|
|
| 查询点处的插入值基于各维中邻点网格点处数值的三次插值。
|
另请参阅
interp1 | interp2 | interp3 | interpn | griddedInterpolant