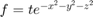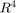interpn

ndgrid 格式的一维、二维、三维和 N 维网格数据的插值

全页折叠

语法

Vq = interpn(X1,X2,...,Xn,V,Xq1,Xq2,...,Xqn)

Vq = interpn(V,Xq1,Xq2,...,Xqn)

Vq = interpn(V)

Vq = interpn(V,k)

Vq = interpn(___,method)

Vq = interpn(___,method,extrapval)

说明

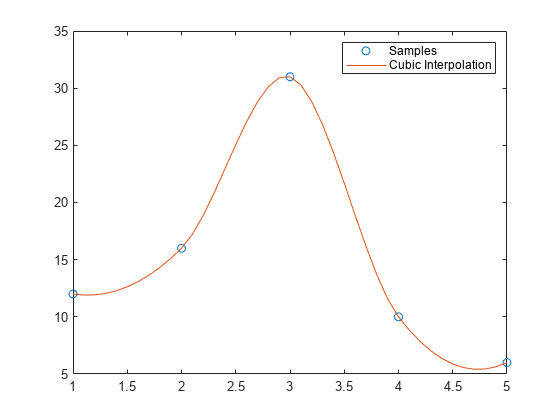
Vq = interpn(X1,X2,...,Xn,V,Xq1,Xq2,...,Xqn) 使用线性插值返回 n 变量函数在特定查询点的插入值。结果始终穿过函数的原始采样。X1,X2,...,Xn 包含样本点的坐标。V 包含各样本点处的对应函数值。Xq1,Xq2,...,Xqn 包含查询点的坐标。

示例

Vq = interpn(V,Xq1,Xq2,...,Xqn) 假定一个默认的样本点网格。默认网格的每个维度均包含点 1,2,3,...n_i。n_i 的值为 V 中第 i 个维度的长度。如果您希望节省内存且不在意点之间的绝对距离，则可使用此语法。

Vq = interpn(V) 将每个维度上样本值之间的间隔分割一次，形成细化网格，并基于该网格上返回插入值。

Vq = interpn(V,k) 将每个维度上样本值之间的间隔反复分割 k 次，形成细化网格，并基于该网格上返回插入值。这将在样本值之间生成 2^k-1 个插值点。

示例

Vq = interpn(___,method) 指定备选插值方法：'linear'、'nearest'、'pchip'、'cubic'、'makima' 或 'spline'。默认方法为 'linear'。

示例

Vq = interpn(___,method,extrapval) 还指定标量值 extrapval，此参数会为处于样本点域范围外的所有查询点赋予该标量值。

如果您为样本点域范围外的查询省略 extrapval 参量，则基于 method 参量，interpn 返回下列值之一：

对于 'spline' 和 'makima' 方法，返回外插值
对于其他内插方法，返回 NaN 值

示例

全部折叠

一维插值

打开实时脚本

定义样本点和值。

x = [1 2 3 4 5];
v = [12 16 31 10 6];

定义查询点 xq 并插值。

xq = (1:0.1:5);
vq = interpn(x,v,xq,'cubic');

绘制结果。

figure
plot(x,v,'o',xq,vq,'-');
legend('Samples','Cubic Interpolation');

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Samples, Cubic Interpolation.

二维插值

打开实时脚本

创建一组一维网格点和对应的样本值。

[X1,X2] = ndgrid((-5:1:5));
R = sqrt(X1.^2 + X2.^2)+ eps;
V = sin(R)./(R);

使用 ntimes=1 在更精细的网格上插值。

Vq = interpn(V,'cubic');
mesh(Vq);

Figure contains an axes object. The axes object contains an object of type surface.

对两组二维采样值进行插值

打开实时脚本

使用 ndgrid 创建一个二维采样点网格。

[x,y] = ndgrid(0:10,0:5);

在采样点处创建两组不同采样值，并将它们串联成三维数组中的页。绘制两组采样值对采样点的图。由于 surf 对网格使用 meshgrid 格式，需要转置输入以进行绘图。

v1 = sin(x.*y)./(x+1);
v2 = x.*erf(y);
V = cat(3,v1,v2);
tiledlayout(1,2)
nexttile
surf(x',y',V(:,:,1)')
view(2)
nexttile
surf(x',y',V(:,:,2)')
view(2)

Figure contains 2 axes objects. Axes object 1 contains an object of type surface. Axes object 2 contains an object of type surface.

使用 ndgrid 创建一组用于插值的查询点，然后使用 interpn 求出每个函数在查询点处的值。绘制插值对查询点的图。

[xq,yq] = ndgrid(0:0.2:10);
Vq = interpn(x,y,V,xq,yq);
tiledlayout(1,2)
nexttile
surf(xq',yq',Vq(:,:,1)')
view(2)
nexttile
surf(xq',yq',Vq(:,:,2)')
view(2)

Figure contains 2 axes objects. Axes object 1 contains an object of type surface. Axes object 2 contains an object of type surface.

在三维函数域范围外执行计算

打开实时脚本

创建网格向量 x1、x2 和 x3。这些向量用于定义与 V 中的值关联的点。

x1 = 1:100;
x2 = 1:50;
x3 = 1:30;

将采样值定义为一个 100×50×30 随机数数组 V。

rng default
V = rand(100,50,30);

计算 x1、x2 和 x3 域范围外三个点处的 V。指定 extrapval = -1。

xq1 = [0 0 0];
xq2 = [0 0 51];
xq3 = [0 101 102];
vq = interpn(x1,x2,x3,V,xq1,xq2,xq3,'linear',-1)

vq = 1×3

    -1    -1    -1

三个点计算得到的值均为 -1，因为它们位于 x1、x2 和 x3 域之外。

四维插值

打开脚本

定义表示 $f = te^{-x^{2}-y^{2}-z^{2}}$ 的匿名函数。

f = @(x,y,z,t) t.*exp(-x.^2 - y.^2 - z.^2);

在 $R^4$ 中创建网格点。然后，将这些点全部传递给函数，以创建样本值 V。

[x,y,z,t] = ndgrid(-1:0.2:1,-1:0.2:1,-1:0.2:1,0:2:10);
V = f(x,y,z,t);

现在创建查询网格。

[xq,yq,zq,tq] = ...
ndgrid(-1:0.05:1,-1:0.08:1,-1:0.05:1,0:0.5:10);

在查询点处进行 V 插值。

Vq = interpn(x,y,z,t,V,xq,yq,zq,tq);

创建影片以显示结果。

figure;
nframes = size(tq, 4);
for j = 1:nframes
   slice(yq(:,:,:,j),xq(:,:,:,j),zq(:,:,:,j),...
         Vq(:,:,:,j),0,0,0);
   clim([0 10]);
   M(j) = getframe;
end
movie(M);

输入参数

全部折叠

`X1,X2,...,Xn` — 样本网格点
数组 | 向量

样本网格点，指定为实数数组或向量。样本网格点必须是唯一的。

如果 X1,X2,...,Xn 是数组，则包含完整网格（ndgrid 格式）的坐标。使用 ndgrid 函数同时创建 X1,X2,...,Xn 数组。这些数组的大小必须相同。
如果 X1,X2,...,Xn 是向量，则将被视作网格向量。这些向量中的值必须严格单调递增或递减。

示例: [X1,X2,X3,X4] = ndgrid(1:30,-10:10,1:5,10:13)

数据类型: single | double

`V` — 样本值
数组

样本值，指定为实数或复数数组。V 的大小要求取决于 X1,X2,...,Xn 定义的采样点网格的大小。采样点 X1,X2,...,Xn 可以是数组或网格向量，但在这两种情况下，它们都定义 n 维网格。V 必须为具有至少相同 n 个维度大小的数组，但它也可以具有超出 n 个维度的额外维度：

如果 V 也有 n 个维度，则 V 的大小必须与 X1,X2,...,Xn 定义的 n 维网格的大小匹配。在本例中，V 在采样点处包含一组采样值。例如，如果 X1,X2,X3 是 3×3×3 数组，则 V 也可以是 3×3×3 数组。
如果 V 的维数超过 n，则 V 的前 n 个维度必须与 X1,X2,...,Xn 定义的 n 维网格的大小匹配。V 中的额外维度定义采样点处的额外采样值集。例如，如果 X1,X2,X3 是 3×3×3 数组，则 V 可以是 3×3×3×2 数组以在采样点处定义两组采样值。

如果 V 包含复数，则 interpn 将分别对实部和虚部插值。

示例: rand(10,5,3,2)

数据类型: single | double
复数支持: 是

`Xq1,Xq2,...,Xqn` — 查询点
标量 | 向量 | 数组

查询点，指定为实数标量、向量或数组。

如果 Xq1,Xq2,...,Xqn 是标量，则为 Rⁿ 中单个查询点的坐标。
如果 Xq1,Xq2,...,Xqn 是方向不同的向量，则 Xq1,Xq2,...,Xqn 将被视作 Rⁿ 中的网格向量。
如果 Xq1,Xq2,...,Xqn 是大小和方向都相同的向量，则 Xq1,Xq2,...,Xqn 将被视作 Rⁿ 中的散点。
如果 Xq1,Xq2,...,Xqn 是大小相同的数组，则表示 Rⁿ 中由查询点构成的一个完整网格（ndgrid 格式）或多个散点。

示例: [X1,X2,X3,X4] = ndgrid(1:10,1:5,7:9,10:11)

数据类型: single | double

`k` — 细化因子
`1` (默认) | 非负实整数标量

细化因子，指定为非负实整数标量。此值指定对每个维度上网格点之间的间隔重复分割优化的次数。这将在样本值之间生成 2^k-1 个插值点。

如果 k 为 0，则 Vq 与 V 相同。

interpn(V,1) 与 interpn(V) 相同。

下面的插图描绘了在 R² 上，k=2 时的情形。共有 72 个插入值（以红色表示）和 9 个样本值（以黑色表示）。

Nine sample points in a grid with three interpolated points between the sample points in each dimension

示例: interpn(V,2)

数据类型: single | double

`method` — 插值方法
`'linear'` (默认) | `'nearest'` | `'pchip'` | `'cubic'` | `'spline'` | `'makima'`

插值方法，指定为下表中的选项之一。

方法	描述	连续性	注释
`'linear'`	查询点处的插入值基于各维中邻近网格点处数值的线性插值。这是默认插值方法。	C⁰	每个维度需要至少两个网格点比 `'nearest'` 需要更多内存
`'nearest'`	查询点处的插入值是距样本网格点最近的值。	不连续	每个维度需要两个网格点。内存要求最低，计算速度最快
`'pchip'`	保形分段三次插值（仅限一维）。查询点处的插入值基于邻近网格点处数值的保形分段三次插值。	C¹	需要至少四个点比 `'linear'` 需要更多内存和计算时间
`'cubic'`	查询点处的插入值基于各维中邻近网格点处数值的三次插值。插值基于三次卷积。	C¹	每个维度中的网格必须有均匀间距，但并非所有维度的网格间距都必须相同每个维度需要至少四个点比 `'linear'` 需要更多内存和计算时间
`'makima'`	修正 Akima 三次 Hermite 插值。查询点的插入值使用次数最大为 3 的分段多项式函数基于各维中邻近网格点的值进行计算而得。为防过冲，已修正 Akima 公式。	C¹	每一维需要至少 2 个点。产生的波动比 `'spline'` 小计算时间通常少于 `'spline'`，但内存要求类似
`'spline'`	查询点处的插入值基于各维中邻近网格点处数值的三次插值。插值基于使用非节点终止条件的三次样条。	C²	每个维度中需要至少 4 个点，如果分别提供 2 个或 3 个点，则退回到线性插值或二次插值比 `'cubic'` 需要更多内存和计算时间

`extrapval` — `X1,X2,...,Xn` 域范围外的函数值
标量

X1,X2,...,Xn 域范围外的函数值，指定为实数或复数标量。interpn 为 X1,X2,...,Xn 域范围外的所有点返回此常量值。

示例: 5

示例: 5+1i

数据类型: single | double
复数支持: 是

输出参量

全部折叠

`Vq` — 插入的值
标量 | 向量 | 数组

插入的值，以实数或复数标量、向量或数组的形式返回。Vq 的大小和形状取决于所用的语法以及（某些情况下）输入参量的大小和值。

如果用 X1,X2,...,Xn 指定采样点，或使用默认网格，并且 V 与采样点的 n 维网格具有相同的维数，则 Vq 包含由 Xq1,Xq2,...,Xqn 定义的查询点处的一组插值。
- 如果 Xq1,Xq2,...,Xqn 是标量，则 Vq 是标量。
- 如果 Xq1,Xq2,...,Xqn 是大小和方向相同的向量，则 Vq 是大小和方向相同的向量。
- 如果 Xq1,Xq2,...,Xqn 是混合方向的网格向量，则 Vq 是与网格向量隐式定义的网格大小相同的数组。
- 如果 Xq1,Xq2,...,Xqn 是大小相同的数组，则 Vq 是大小相同的数组。
如果用 X1,X2,...,Xn 指定采样点，或使用默认网格，并且 V 的维数多于采样点的 n 维网格，则 Vq 包含由 Xq1,Xq2,...,Xqn 定义的查询点处的多组插值。在这种情况下，Vq 的前 n 个维度遵循上述单组插值的大小规则，但 Vq 也具有与 V 大小相同的额外维度。
使用语法 interpn(V) 和 interpn(V,k)，插值是通过对默认网格进行 k 次细分来执行的（其中对于 interpn(V) 来说，k=1）。在这种情况下，Vq 是与 V 具有相同维数的数组，其中第 I 维的大小为 2^k * (size(V,i)-1)+1。

详细信息

全部折叠

严格单调

一组始终递减或递增且无反转的值。例如，序列 a = [2 4 6 8] 便是一个严格单调递增的序列。序列 b = [2 4 4 6 8] 则非严格单调，因为 b(2) 与 b(3) 之间的值无变化。而序列 c = [2 4 6 8 6] 在 c(4) 与 c(5) 之间包含反转，因此连单调序列也不是。

完整网格（ndgrid 格式）

对 interpn 而言，完整网格包含 n 个数组 X1,X2,...,Xn，其元素表示 Rⁿ 中的网格点。第 i 个数组 X_i 包含沿第 i 个维度变化最快的严格单调递增值。

使用 ndgrid 函数创建可传递至 interpn 的完整网格。例如，以下代码便在 R² 中为区域 1 ≤ X1 ≤ 3、1≤ X2 ≤ 4 创建了一个完整网格。

[X1,X2] = ndgrid(-1:3,(1:4))

X1 =

    -1    -1    -1    -1
     0     0     0     0
     1     1     1     1
     2     2     2     2
     3     3     3     3


X2 =

     1     2     3     4
     1     2     3     4
     1     2     3     4
     1     2     3     4
     1     2     3     4

网格向量

对 interpn 而言，网格向量由 n 个具有混合方向的向量组成，这些向量用于定义 Rⁿ 中的网格点。

例如，以下代码在 R³ 中为区域 1 ≤ x1 ≤ 3、4 ≤ x2 ≤ 5 和 6 ≤x3≤ 8 创建网格向量：

x1 = 1:3;
x2 = (4:5)';
x3 = 6:8;

散点

对 interpn 而言，散点由 n 个定义 Rⁿ 散点集合的数组或向量 Xq1,Xq2,...,Xqn 组成。第 i 个数组 Xi 包含第 i 个维度的坐标。

例如，以下代码指定 R³ 中的点 (1, 19, 10)、(6, 40, 1)、(15, 33, 22) 和 (0, 61, 13)。

Xq1 = [1 6; 15 0];
Xq2 = [19 40; 33 61];
Xq3 = [10 1; 22 13];

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

为了获得最佳结果，请以向量的形式提供 X1,X2,...,Xn。这些向量的值必须严格单调递增。
代码生成不支持 'makima' 插值方法。
插值方法必须为常量字符向量。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

interpn 函数支持 GPU 数组输入，但有以下用法说明和限制：

最多支持五个维度。
X1,X2,...,Xn 的维度必须与 V 一致。
method 必须是 'linear' 或 'nearest'。

有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

用法说明和限制：

X1,X2,...,Xn 的维度必须与 V 一致。

有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

全部展开

R2021a: 同时对多个数据集进行插值

增加了在同一网格上的相同查询点处对多个数据集进行插值的支持。例如，如果指定一个二维网格、一个由网格点处的值组成三维数组，以及一个二维查询点集合，则 interpn 将为三维值数组中每个二维页返回查询点处的插值。

另请参阅

interp1 | interp2 | interp3 | ndgrid

interpn

语法

说明

示例

一维插值

二维插值

对两组二维采样值进行插值

在三维函数域范围外执行计算

四维插值

输入参数

X1,X2,...,Xn — 样本网格点 数组 | 向量

V — 样本值 数组

Xq1,Xq2,...,Xqn — 查询点 标量 | 向量 | 数组

k — 细化因子 1 (默认) | 非负实整数标量

method — 插值方法 'linear' (默认) | 'nearest' | 'pchip' | 'cubic' | 'spline' | 'makima'

extrapval — X1,X2,...,Xn 域范围外的函数值 标量

输出参量

Vq — 插入的值 标量 | 向量 | 数组

详细信息

严格单调

完整网格（ndgrid 格式）

网格向量

散点

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

R2021a: 同时对多个数据集进行插值

另请参阅

`X1,X2,...,Xn` — 样本网格点
数组 | 向量

`V` — 样本值
数组

`Xq1,Xq2,...,Xqn` — 查询点
标量 | 向量 | 数组

`k` — 细化因子
`1` (默认) | 非负实整数标量

`method` — 插值方法
`'linear'` (默认) | `'nearest'` | `'pchip'` | `'cubic'` | `'spline'` | `'makima'`

`extrapval` — `X1,X2,...,Xn` 域范围外的函数值
标量

`Vq` — 插入的值
标量 | 向量 | 数组

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。