scatteredInterpolant

对二维或三维散点数据插值

说明

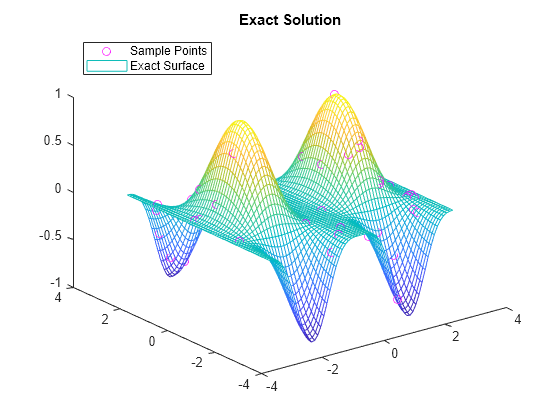
使用 scatteredInterpolant 对散点数据的二维或三维数据集执行插值。scatteredInterpolant 返回给定数据集的插值 F。您可以计算一组查询点（例如二维 (xq,yq)）处的 F 值，以得出插入的值 vq = F(xq,yq)。

使用 griddedInterpolant 对网格数据执行插值。

创建对象

语法

F = scatteredInterpolant

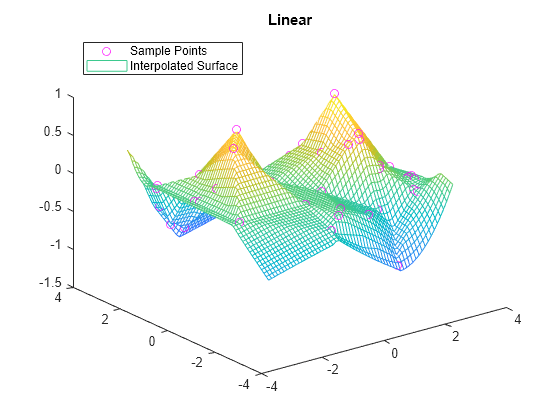
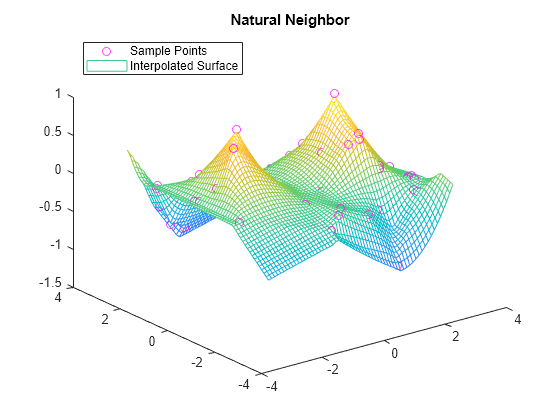
F = scatteredInterpolant(x,y,v)

F = scatteredInterpolant(x,y,z,v)

F = scatteredInterpolant(P,v)

F = scatteredInterpolant(___,Method)

F = scatteredInterpolant(___,Method,ExtrapolationMethod)

描述

F = scatteredInterpolant 创建一个空的散点数据插值对象。

F = scatteredInterpolant(x,y,v) 创建一个拟合 v = F(x,y) 形式的曲面的插值。向量 x 和 y 指定样本点的 (x,y) 坐标。v 包含与点 (x,y) 关联的样本值。

示例

F = scatteredInterpolant(x,y,z,v) 创建一个 v = F(x,y,z) 形式的三维插值。

示例

F = scatteredInterpolant(P,v) 以数组形式指定样本点坐标。P 的行包含 v 中值的 (x, y) 或 (x, y, z) 坐标。

示例

F = scatteredInterpolant(___,Method) 在前三个语法中的任意一个中指定插值方法 'nearest'、'linear' 或 'natural' 作为最后一个输入参量。

示例

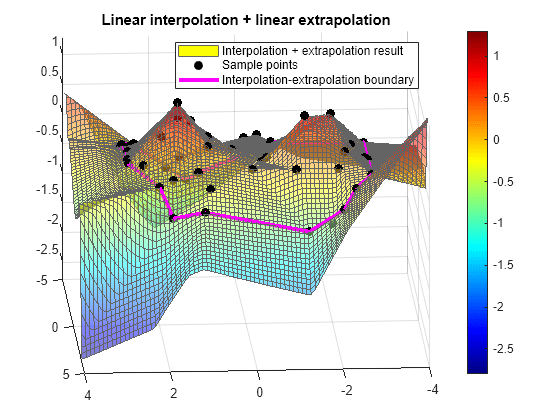
F = scatteredInterpolant(___,Method,ExtrapolationMethod) 指定内插和外插方法。在前三个语法的任意一个中同时传递 Method 和 ExtrapolationMethod 作为最后两个输入参量。

示例

输入参量

全部展开

`x`, `y`, `z` — 样本点
列向量

样本点，指定为列向量，其行数与 v 相同。样本点应该是唯一的。但是，如果样本点包含重复项，scatteredInterpolant 将显示警告并将重复项合并为单个点。

x、y 和 z 参量设置 scatteredInterpolant 对象的 Points 属性的值。

数据类型: double

`P` — 样本点数组
矩阵

样本点数组，指定为 m×n 的矩阵，其中 m 是点数，n 是这些点所在空间的维度。P 的各行包含样本点的 (x, y) 或 (x, y, z) 坐标。样本点应该是唯一的。但是，如果样本点包含重复项，scatteredInterpolant 将显示警告并将重复项合并为单个点。

此参量设置 scatteredInterpolant 对象的 Points 属性。

数据类型: double

`v` — 样本点处的函数值
向量 | 矩阵

样本点处的函数值，指定为向量或矩阵。对于二维数据，v = F(x,y)。对于三维数据，v = F(x,y,z)。

要使用一组值进行插值，请将 v 指定为向量，其中行数与样本点数相同。
要使用多组值进行插值，请将 v 指定为矩阵，其中行数与样本点数相同。v 中的每列表示不同函数在样本点的值。例如，如果 x 和 y 是包含 10 个元素的列向量，则可以将 v 指定为 10×4 矩阵以使用四组不同值进行插值。

scatteredInterpolant 不会忽略 v 中的 NaN 值，因此那些采样点附近的插值结果也是 NaN。

此参量设置 scatteredInterpolant 对象的 Values 属性。

数据类型: double

`Method` — 插值方法
`'linear'` (默认) | `'nearest'` | `'natural'`

插值方法，指定为下列选项之一。

方法	描述	连续性
`'linear'`（默认值）	线性插值	C⁰
`'nearest'`	最近邻点插值	不连续
`'natural'`	自然邻点插值	C¹（样本点处除外）

此参量设置 scatteredInterpolant 对象的 Method 属性。

`ExtrapolationMethod` — 外插方法
`'linear'` | `'nearest'` | `'boundary'` | `'none'`

外插法，指定为下列选项之一。

外插方法	描述
`'linear'`	基于边界梯度的线性外插。当 `Method` 为 `'linear'` 或 `'natural'` 时，此方法是默认方法。
`'nearest'`	最近邻点外插。此方法的计算结果为最近邻点的值。当 `Method` 为 `'nearest'` 时，此方法是默认方法。
`'boundary'` (自 R2024a 起)	边界外插。此方法可将内插边界上的值扩展到外插域中。
`'none'`	无外插。`Points` 凸包之外的任何查询返回 `NaN`。

此参量设置 scatteredInterpolant 对象的 ExtrapolationMethod 属性。

属性

全部展开

`Points` — 样本点
矩阵

样本点，指定为一个矩阵。该矩阵的大小为 m×2 或 m×3，表示二维或三维空间中的 m 个点。Points 的各行包含唯一样本点的 (x, y) 或 (x, y, z) 坐标。Points 中的行对应于 Values 中的函数值。

数据类型: double

`Values` — 样本点处的函数值
向量 | 矩阵

样本点处的函数值，指定为向量或矩阵。此属性由 v 输入参量设置。

数据类型: double

`Method` — 插值方法
`'linear'` (默认) | `'nearest'` | `'natural'`

插值方法，指定为 'linear'、'nearest' 或 'natural'。有关这些方法的说明，请参阅 Method。

`ExtrapolationMethod` — 外插方法
`'linear'` | `'nearest'` | `'boundary'` | `'none'`

外插方法，指定为 'linear'、'nearest'、'boundary' (自 R2024a 起) 或 'none'。有关这些方法的说明，请参阅 ExtrapolationMethod。

用途

语法

Vq = F(Pq)

Vq = F(Xq,Yq)

Vq = F(Xq,Yq,Zq)

Vq = F({xq,yq})

Vq = F({xq,yq,zq})

描述

使用 scatteredInterpolant 创建插值 F。然后，您可以使用以下任何语法在特定点处计算 F。

Vq = F(Pq) 在矩阵 Pq 中的查询点处对 F 求值。Pq 中的每行都包含查询点的坐标。

Vq = F(Xq,Yq) 和 Vq = F(Xq,Yq,Zq) 将查询点指定为两个或三个大小相等的数组。F 将查询点视为列向量，例如，Xq(:)。

如果 F 的 Values 属性是表示样本点处的一组值的列向量，则 Vq 与查询点的大小相同。
如果 F 的 Values 属性是表示样本点处多组值的矩阵，则 Vq 是矩阵，每列表示查询点处不同的一组值。

示例

Vq = F({xq,yq}) 和 Vq = F({xq,yq,zq}) 将查询点指定为网格向量。使用此语法可在您要查询大型点网格时节省内存。

示例

全部折叠

二维插值

打开实时脚本

定义一些样本点，并计算这些位置的三角函数的值。这些点是用于插值的样本值。

t = linspace(3/4*pi,2*pi,50)';
x = [3*cos(t); 2*cos(t); 0.7*cos(t)];
y = [3*sin(t); 2*sin(t); 0.7*sin(t)];
v = repelem([-0.5; 1.5; 2],length(t));

创建插值。

F = scatteredInterpolant(x,y,v);

计算位于查询位置 (xq, yq) 处的插值。

tq = linspace(3/4*pi+0.2,2*pi-0.2,40)';
xq = [2.8*cos(tq); 1.7*cos(tq); cos(tq)];
yq = [2.8*sin(tq); 1.7*sin(tq); sin(tq)];
vq = F(xq,yq);

绘制结果。

plot3(x,y,v,'.',xq,yq,vq,'.'), grid on
title('Linear Interpolation')
xlabel('x'), ylabel('y'), zlabel('Values')
legend('Sample data','Interpolated query data','Location','Best')

三维插值

打开实时脚本

为一组散点样本点创建插值，然后计算一组三维查询点处的插值。

定义 200 个随机点并对三角函数采样。这些点是用于插值的样本值。

rng default;
P = -2.5 + 5*rand([200 3]);
v = sin(P(:,1).^2 + P(:,2).^2 + P(:,3).^2)./(P(:,1).^2+P(:,2).^2+P(:,3).^2);

创建插值。

F = scatteredInterpolant(P,v);

计算位于查询位置 (xq,yq,zq) 处的插值。

[xq,yq,zq] = meshgrid(-2:0.25:2);
vq = F(xq,yq,zq);

绘制结果的切片。

xslice = [-.5,1,2]; 
yslice = [0,2]; 
zslice = [-2,0];
slice(xq,yq,zq,vq,xslice,yslice,zslice)

替代样本值

打开实时脚本

在需要更改位于样本点处的值时替换 Values 属性中的元素。由于原始三角剖分没有改变，因此您在计算新插值时可立即获得结果。

创建 50 个随机点并对指数函数进行采样。这些点是用于插值的样本值。

rng('default')
x = -2.5 + 5*rand([50 1]);
y = -2.5 + 5*rand([50 1]);
v = x.*exp(-x.^2-y.^2);

创建插值。

F = scatteredInterpolant(x,y,v)

F = 
  scatteredInterpolant with properties:

                 Points: [50x2 double]
                 Values: [50x1 double]
                 Method: 'linear'
    ExtrapolationMethod: 'linear'

在 (1.40,1.90) 处计算插值。

F(1.40,1.90)

ans = 0.0069

更改插值样本值，并重新计算同一点处的插值。

vnew = x.^2 + y.^2;
F.Values = vnew;
F(1.40,1.90)

ans = 5.6491

消除重复的采样点

打开实时脚本

使用 groupsummary 消除重复的采样点，并在调用 scatteredInterpolant 之前控制其合并方式。

创建一个由采样点位置组成的 200×3 矩阵。在最后五行添加重复的点。

P = -2.5 + 5*rand(200,3);
P(197:200,:) = repmat(P(196,:),4,1);

创建一个由采样点上的随机值组成的向量。

V = rand(size(P,1),1);

如果您尝试对重复采样点使用 scatteredInterpolant，它会引发警告，并对 V 中的对应值求平均值以产生一个唯一点。但您可以在创建插值之前使用 groupsummary 来消除重复点。如果要使用求平均值以外的方法合并重复点，此操作尤其有用。

使用 groupsummary 消除重复采样点，并在重复采样点位置保留 V 中的最大值。指定采样点矩阵作为分组变量，指定对应值作为数据。

[V_unique,P_unique] = groupsummary(V,P,@max);

由于分组变量有三列，groupsummary 以元胞数组形式返回唯一组 P_unique。将元胞数组转换回矩阵。

P_unique = [P_unique{:}];

创建插值。由于采样点现在是唯一的，scatteredInterpolant 不会发出警告。

I = scatteredInterpolant(P_unique,V_unique);

比较散点数据的插值方法

打开实时脚本

比较 scatteredInterpolant 提供的几种不同插值算法的结果。

创建包含 50 个散点的样本数据集。这里有意使用较少的点数量，目的是为了突出插值方法之间的差异。

x = -3 + 6*rand(50,1);
y = -3 + 6*rand(50,1);
v = sin(x).^4 .* cos(y);

创建插值和查询点网格。

F = scatteredInterpolant(x,y,v);
[xq,yq] = meshgrid(-3:0.1:3);

使用 'nearest'、'linear' 和 'natural' 方法绘制结果图。每当插值方法更改时，您都需要重新查询插值以获取更新后的结果。

F.Method = 'nearest';
vq1 = F(xq,yq);
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq1)
title('Nearest Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

F.Method = 'linear';
vq2 = F(xq,yq);
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq2)
title('Linear')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

F.Method = 'natural';
vq3 = F(xq,yq);
figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq3)
title('Natural Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')

绘制精确解。

figure
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,sin(xq).^4 .* cos(yq))
title('Exact Solution')
legend('Sample Points','Exact Surface','Location','NorthWest')

比较散点数据的外插方法

自 R2024a 起

打开实时脚本

比较 scatteredInterpolant 提供的几种不同外插方法的结果。

创建一个由 50 个散点组成的样本数据集，并计算在这些位置的三角函数的值。这些点是用于插值的样本值。

rng default
x = -3 + 6*rand(50,1);
y = -3 + 6*rand(50,1);
v = sin(x).^4 .* cos(y);

创建插值。

F = scatteredInterpolant(x,y,v)

F = 
  scatteredInterpolant with properties:

                 Points: [50x2 double]
                 Values: [50x1 double]
                 Method: 'linear'
    ExtrapolationMethod: 'linear'

计算输入数据的边界。

C = convhull(x,y);
xc = [x(C); x(C(1))];
yc = [y(C); y(C(1))];
vc = [v(C); v(C(1))];

使用基于边界梯度的线性外插方法计算在查询位置 (xq,yq) 处的插值。然后，绘制内插和外插的结果。

[xq,yq] = meshgrid(-4:0.1:4);
vq1 = F(xq,yq);

surf(xq,yq,vq1,FaceAlpha=0.5,DisplayName="Interpolation + extrapolation result",EdgeColor=[100 100 100]./256,FaceColor="interp")
hold on
plot3(x,y,v,"black.",MarkerSize=20,DisplayName="Sample points")
plot3(xc,yc,vc,"magenta-",LineWidth=3,DisplayName="Interpolation-extrapolation boundary")
title("Linear interpolation + linear extrapolation")
legend(Location="NorthEast")
zlim([-2.8 1.3])
colorbar
colormap jet
clim([-2.8 1.3])
view([-183.69 21.20])
hold off

修改内插以使用最近邻外插，并计算和可视化内插。

F.ExtrapolationMethod = "nearest";
vq2 = F(xq,yq);

surf(xq,yq,vq2,FaceAlpha=0.5,DisplayName="Interpolation + extrapolation result",EdgeColor=[100 100 100]./256,FaceColor="interp")
hold on
plot3(x,y,v,"black.",MarkerSize=20,DisplayName="Sample points")
plot3(xc,yc,vc,"magenta-",LineWidth=3,DisplayName="Interpolation-extrapolation boundary")
title("Linear interpolation + Nearest extrapolation")
legend(Location="NorthEast")
zlim([-2.8 1.3])
colorbar
colormap jet
clim([-2.8 1.3])
view([-183.69 21.20])
hold off

修改内插以将内插边界扩展到外插域中，并计算和可视化内插。

F.ExtrapolationMethod = "boundary";
vq3 = F(xq,yq);

surf(xq,yq,vq3,FaceAlpha=0.5,DisplayName="Interpolation + extrapolation result",EdgeColor=[100 100 100]./256,FaceColor="interp")
hold on
plot3(x,y,v,"black.",MarkerSize=20,DisplayName="Sample points")
plot3(xc,yc,vc,"magenta-",LineWidth=3,DisplayName="Interpolation-extrapolation boundary")
title("Linear interpolation + Boundary extrapolation")
legend(Location="NorthEast")
zlim([-2.8 1.3])
colorbar
colormap jet
clim([-2.8 1.3])
view([-183.69 21.20])
hold off

通过检查绘制的结果来比较外插方法。边界外插会保持内插和外插域之间的连续性，而最近邻外插沿边界可能是不连续的。边界外插不会在外插域中产生极值，而线性外插会产生极值。

在查询点进行多组值插值

自 R2023b 起

打开实时脚本

在相同的查询点对多个数据集进行插值。

创建一个包含 50 个散点的样本数据集，由样本点向量 x 和 y 表示。

rng("default")
x = -3 + 6*rand(50,1);
y = -3 + 6*rand(50,1);

要对多个数据集进行插值，请创建一个矩阵，其中每列表示不同函数在样本点的值。

s1 = sin(x).^4 .* cos(y);
s2 = sin(x) + cos(y);
s3 = x + y;
s4 = x.^2 + y;
v = [s1 s2 s3 s4];

创建查询点向量，指示为 v 中的每组值执行插值的位置。

xq = -3:0.1:3;
yq = -3:0.1:3;

创建插值 F。

F = scatteredInterpolant(x,y,v)

F = 
  scatteredInterpolant with properties:

                 Points: [50x2 double]
                 Values: [50x4 double]
                 Method: 'linear'
    ExtrapolationMethod: 'linear'

计算位于查询位置的插值。Vq 的每页都包含 v 中对应数据集的插值。

Vq = F({xq,yq});
size(Vq)

ans = 1×3

    61    61     4

绘制每个数据集的插值。

tiledlayout(2,2)
nexttile
plot3(x,y,v(:,1),'mo')
hold on
mesh(xq,yq,Vq(:,:,1)')
title("sin(x).^4 .* cos(y)")

nexttile
plot3(x,y,v(:,2),'mo')
hold on
mesh(xq,yq,Vq(:,:,2)')
title("sin(x) + cos(y)")

nexttile
plot3(x,y,v(:,3),'mo')
hold on
mesh(xq,yq,Vq(:,:,3)')
title("x + y")

nexttile
plot3(x,y,v(:,4),'mo')
hold on
mesh(xq,yq,Vq(:,:,4)')
title("x.^2 + y")

lg = legend("Sample Points","Interpolated Surface");
lg.Layout.Tile = "north";

详细信息

全部展开

插值

可在查询点计算的插值函数。

网格数据

一组轴对齐的有序点。

散点数据

在其相对位置没有结构体的一组点。

完整网格

表示为一组数组的网格。例如，您可以使用 ndgrid 创建完整网格。

网格向量

充当 ndgrid 格式的网格的紧凑表示形式的向量组。

例如，[X,Y] = ndgrid(xg,yg) 在矩阵 X 和 Y 中返回完整网格。您可以使用网格向量 xg 和 yg 表示同一网格。

提示

计算多组不同查询点处的 scatteredInterpolant 对象 F 的值比使用函数 griddata 或 griddatan 单独计算插值的速度更快。例如：

% Fast to create interpolant F and evaluate multiple times
F = scatteredInterpolant(X,Y,V)
v1 = F(Xq1,Yq1)
v2 = F(Xq2,Yq2)

% Slower to compute interpolations separately using griddata
v1 = griddata(X,Y,V,Xq1,Yq1)
v2 = griddata(X,Y,V,Xq2,Yq2)

要更改插值样本值或插值方法，更新插值对象 F 的属性比创建新 scatteredInterpolant 对象的效率更高。当您更新 Values 或 Method 时，输入数据的基础德劳内三角剖分不会更改，因此您可以快速计算新结果。
使用 scatteredInterpolant 进行的散点数据插值使用数据的德劳内三角剖分，因此插值对样本点 x、y、z 或 P 中的缩放问题非常敏感。出现缩放问题时，您可以使用 normalize 重新缩放数据并改进结果。有关详细信息，请参阅对不同量级的数据进行归一化。

算法

scatteredInterpolant 使用散点样本点的德劳内三角剖分执行插值 [1]。

参考

[1] Amidror, Isaac. “Scattered data interpolation methods for electronic imaging systems: a survey.” Journal of Electronic Imaging. Vol. 11, No. 2, April 2002, pp. 157–176.

扩展功能

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

版本历史记录

在 R2013a 中推出

全部展开

R2024a: 使用边界值进行外插

制定 'boundary' 外插方法以将内插边界上的值扩展到外插域中。此方法可减少极值外插值，并保持外插域和内插域之间的连续性。

R2023b: 同时对多个数据集进行插值

将采样值 v 指定为矩阵，以便在相同的查询点处对相同网格上的多个数据集进行插值。v 中的每列表示不同函数在样本点的值。例如，如果 x 和 y 是包含 10 个元素的列向量，则可以将 v 指定为 10×4 矩阵以使用四组不同值进行插值。

以前，您只能将 v 指定为向量，且多值插值仅适用于 griddedInterpolant。

另请参阅

griddedInterpolant | griddata | griddatan | ndgrid | meshgrid

scatteredInterpolant

说明

创建对象

语法

描述

输入参量

x, y, z — 样本点 列向量

P — 样本点数组 矩阵

v — 样本点处的函数值 向量 | 矩阵

Method — 插值方法 'linear' (默认) | 'nearest' | 'natural'

ExtrapolationMethod — 外插方法 'linear' | 'nearest' | 'boundary' | 'none'

属性

Points — 样本点 矩阵

Values — 样本点处的函数值 向量 | 矩阵

Method — 插值方法 'linear' (默认) | 'nearest' | 'natural'

ExtrapolationMethod — 外插方法 'linear' | 'nearest' | 'boundary' | 'none'

用途

语法

描述

示例

二维插值

三维插值

替代样本值

消除重复的采样点

比较散点数据的插值方法

比较散点数据的外插方法

在查询点进行多组值插值

详细信息

插值

网格数据

散点数据

完整网格

网格向量

提示

算法

参考

扩展功能

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

版本历史记录

R2024a: 使用边界值进行外插

R2023b: 同时对多个数据集进行插值

另请参阅

WeChat

`x`, `y`, `z` — 样本点
列向量

`P` — 样本点数组
矩阵

`v` — 样本点处的函数值
向量 | 矩阵

`Method` — 插值方法
`'linear'` (默认) | `'nearest'` | `'natural'`

`ExtrapolationMethod` — 外插方法
`'linear'` | `'nearest'` | `'boundary'` | `'none'`

`Points` — 样本点
矩阵

`Values` — 样本点处的函数值
向量 | 矩阵

`Method` — 插值方法
`'linear'` (默认) | `'nearest'` | `'natural'`

`ExtrapolationMethod` — 外插方法
`'linear'` | `'nearest'` | `'boundary'` | `'none'`

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。