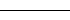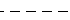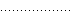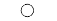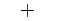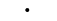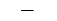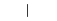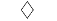Surface 属性
基本曲面的外观和行为
Surface 属性控制 Surface 对象的外观和行为。通过更改属性值,您可以修改曲面图的某些方面。使用圆点表示法查询和设置属性。
s = surface; c = s.CData; s.CDataMapping = 'direct';
面
面颜色,指定为下表中的值之一。
| 值 | 描述 |
|---|---|
'flat' | 根据
|
'interp' | 根据
|
| RGB 三元组、十六进制颜色代码或颜色名称 | 对所有面使用指定的颜色。此选项不会使用
|
'texturemap' | 变换 CData 中的颜色数据,以便其符合曲面。 |
'none' | 不绘制面。 |
RGB 三元组和十六进制颜色代码对于指定自定义颜色非常有用。
RGB 三元组是包含三个元素的行向量,其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内,例如[0.4 0.6 0.7]。十六进制颜色代码是字符向量或字符串标量,以井号 (
#) 开头,后跟三个或六个十六进制数字,范围可以是0到F。这些值不区分大小写。因此,颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外,还可以按名称指定一些常见的颜色。下表列出了命名颜色选项、等效 RGB 三元组和十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如,获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
面透明度,指定为下列值之一:
范围
[0,1]中的标量 - 在所有面上使用统一的透明度。值为1时完全不透明,值为0时完全透明。介于0和1之间的值表示半透明。此选项不会使用AlphaData属性中的透明度值。'flat'- 根据AlphaData属性中的值,对每个面使用不同的透明度。第一个顶点的透明度值确定整个面的透明度。首先您必须将AlphaData属性指定为矩阵,大小与ZData属性相同。FaceColor属性也必须设置为'flat'。'interp'- 根据AlphaData属性中的值,对每个面使用插值透明度。通过基于各顶点处透明度数值进行插值,每个面上的透明度会渐变。首先您必须将AlphaData属性指定为矩阵,大小与ZData属性相同。FaceColor属性也必须设置为'interp'。'texturemap'- 变换AlphaData中的数据,以便其符合曲面。
光源对象对面的影响,指定为下列值之一:
'flat'- 将光源均匀地应用于每个面上。使用此值可查看分面着色对象。'gouraud'- 改变各个面的光源。计算顶点处的光照,然后以在各个面中进行光照插值。使用此值可查看曲面。'none'- 不将来自光源对象的光源应用于各个面。
要向坐标区中添加光对象,请使用 light 函数。
注意
'phong' 值已被删除。请改用 'gouraud'。
顶点法向量远离相机时的面光照,指定为以下值之一:
'reverselit'- 照亮该面,好像顶点法向量指向相机一样。'unlit'- 不照亮该面。'lit'- 根据顶点法向量照亮该面。
使用此属性区别对象的内部曲面和外部曲面。有关示例,请参阅背面光照。
边缘
要显示的边缘,指定为 'both'、'row' 或 'column'。
边线颜色,指定为下面列出的值之一。默认颜色 [0 0 0] 对应于黑边。
| 值 | 描述 |
|---|---|
'none' | 不绘制边。 |
'flat' | 根据
|
'interp' | 根据
|
| RGB 三元组、十六进制颜色代码或颜色名称 | 对所有边使用指定的颜色。此选项不会使用
|
RGB 三元组和十六进制颜色代码对于指定自定义颜色非常有用。
RGB 三元组是包含三个元素的行向量,其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内,例如[0.4 0.6 0.7]。十六进制颜色代码是字符向量或字符串标量,以井号 (
#) 开头,后跟三个或六个十六进制数字,范围可以是0到F。这些值不区分大小写。因此,颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外,还可以按名称指定一些常见的颜色。下表列出了命名颜色选项、等效 RGB 三元组和十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如,获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
边透明度,指定为下列值之一:
[0,1]范围内的标量 - 在所有边上都使用统一的透明度。值为1时完全不透明,值为0时完全透明。介于0和1之间的值表示半透明。此选项不会使用AlphaData属性中的透明度值。'flat'- 根据AlphaData属性中的值,对每个边使用不同透明度。首先您必须将AlphaData属性指定为矩阵,大小与ZData属性相同。第一个顶点上的透明度值确定整条边的透明度。EdgeColor属性也必须设置为'flat'。'interp'- 根据AlphaData属性中的值,对每个边使用插值透明度。首先您必须将AlphaData属性指定为矩阵,大小与ZData属性相同。通过基于各顶点处值进行插值,每条边上的透明度会渐变。EdgeColor属性也必须设置为'interp'。
线型,指定为下表中列出的选项之一。
| 线型 | 描述 | 表示的线条 |
|---|---|---|
"-" | 实线 |
|
"--" | 虚线 |
|
":" | 点线 |
|
"-." | 点划线 |
|
"none" | 无线条 | 无线条 |
线宽,指定为以磅为单位的正值,其中 1 磅 = 1/72 英寸。如果该线条具有标记,则线条宽度也会影响标记边。
线宽不能小于像素的宽度。如果将线宽设置为小于系统上像素宽度的值,则线条显示为一个像素的宽度。
锐化垂直线和水平线,指定为 'on' 或 'off',或指定为数值或逻辑值 1 (true) 或 0 (false)。值 'on' 等效于 true,'off' 等效于 false。因此,您可以使用此属性的值作为逻辑值。该值存储为 matlab.lang.OnOffSwitchState 类型的 on/off 逻辑值。
| 值 | 描述 | 外观 |
|---|---|---|
'on' | 锐化垂直线和水平线以消除外观不均现象。 |
|
'off' | 不锐化垂直线或水平线。线条可能出现不均匀的厚度或颜色。 |
|
光源对象对边缘的影响,指定为下列值之一:
'flat'- 将光源均匀地应用于每个边缘上。'none'- 不将来自光源对象的光源应用于各个边。'gouraud'- 计算顶点处的光源,然后以线性方式插入各个边缘中。
注意
'phong' 值已被删除。请改用 'gouraud'。
标记
标记符号,指定为下表中列出的值之一。默认情况下,对象不显示标记。指定标记符号可在每个数据点或顶点添加标记。
| 标记 | 描述 | 生成的标记 |
|---|---|---|
"o" | 圆圈 |
|
"+" | 加号 |
|
"*" | 星号 |
|
"." | 点 |
|
"x" | 叉号 |
|
"_" | 水平线条 |
|
"|" | 垂直线条 |
|
"square" | 方形 |
|
"diamond" | 菱形 |
|
"^" | 上三角 |
|
"v" | 下三角 |
|
">" | 右三角 |
|
"<" | 左三角 |
|
"pentagram" | 五角形 |
|
"hexagram" | 六角形 |
|
"none" | 无标记 | 不适用 |
标记大小,指定为以磅为单位的正值,其中 1 磅 = 1/72 英寸。
标记轮廓颜色,指定为 'auto'、'flat'、RGB 三元组、十六进制颜色代码、颜色名称或短名称。'auto' 选项使用与 EdgeColor 属性相同的颜色。'flat' 选项使用顶点处的 CData 值设置颜色。
对于自定义颜色,请指定 RGB 三元组或十六进制颜色代码。
RGB 三元组是包含三个元素的行向量,其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内,例如[0.4 0.6 0.7]。十六进制颜色代码是字符串标量或字符向量,以井号 (
#) 开头,后跟三个或六个十六进制数字,范围可以是0到F。这些值不区分大小写。因此,颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外,还可以按名称指定一些常见的颜色。下表列出了一些命名颜色选项、其等效 RGB 三元组及十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | 不适用 | 不适用 | 不适用 | 无颜色 |
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如,获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
标记填充颜色,指定为 'auto'、'flat'、RGB 三元组、十六进制颜色代码、颜色名称或短名称。'auto' 选项使用与坐标区的 Color 属性相同的颜色。'flat' 选项使用顶点处的 CData 值设置颜色。
对于自定义颜色,请指定 RGB 三元组或十六进制颜色代码。
RGB 三元组是包含三个元素的行向量,其元素分别指定颜色中红、绿、蓝分量的强度。强度值必须位于
[0,1]范围内,例如[0.4 0.6 0.7]。十六进制颜色代码是字符串标量或字符向量,以井号 (
#) 开头,后跟三个或六个十六进制数字,范围可以是0到F。这些值不区分大小写。因此,颜色代码"#FF8800"与"#ff8800"、"#F80"与"#f80"是等效的。
此外,还可以按名称指定一些常见的颜色。下表列出了一些命名颜色选项、其等效 RGB 三元组及十六进制颜色代码。
| 颜色名称 | 短名称 | RGB 三元组 | 十六进制颜色代码 | 外观 |
|---|---|---|---|---|
"red" | "r" | [1 0 0] | "#FF0000" |
|
"green" | "g" | [0 1 0] | "#00FF00" |
|
"blue" | "b" | [0 0 1] | "#0000FF" |
|
"cyan" | "c" | [0 1 1] | "#00FFFF" |
|
"magenta" | "m" | [1 0 1] | "#FF00FF" |
|
"yellow" | "y" | [1 1 0] | "#FFFF00" |
|
"black" | "k" | [0 0 0] | "#000000" |
|
"white" | "w" | [1 1 1] | "#FFFFFF" |
|
"none" | 不适用 | 不适用 | 不适用 | 无颜色 |
下表列出了浅色和深色主题中绘图的默认调色板。
| 调色板 | 调色板颜色 |
|---|---|
在 R2025a 之前的版本中: 大多数绘图默认使用这些颜色。 |
|
|
|
您可以使用 orderedcolors 和 rgb2hex 函数获取这些调色板的 RGB 三元组和十六进制颜色代码。例如,获取 "gem" 调色板的 RGB 三元组并将其转换为十六进制颜色代码。
RGB = orderedcolors("gem");
H = rgb2hex(RGB);在 R2023b 之前的版本中: 使用 RGB = get(groot,"FactoryAxesColorOrder") 获取 RGB 三元组。
在 R2024a 之前的版本中: 使用 H = compose("#%02X%02X%02X",round(RGB*255)) 获取十六进制颜色代码。
此属性仅影响圆形、方形、菱形、五角形、六角形和四个三角形标记类型。
示例: [0.3 0.2 0.1]
示例: 'green'
示例: '#D2F9A7'
笛卡尔坐标数据
x 坐标数据,指定为大小与 ZData 相同的矩阵或 length(n) 向量,其中 [m,n] = size(ZData)。
数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
XData 的选择模式,指定为下列值之一:
'auto'- 使用ZData的列索引。'manual'- 使用手动指定的值。要指定值,请将输入参量传递给绘图函数或直接设置XData属性。
y 坐标数据,指定为大小与 ZData 相同的矩阵或 length(m) 向量,其中 [m,n] = size(ZData)。
数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
YData 的选择模式,指定为下列值之一:
'auto'- 使用ZData的行索引。'manual'- 使用手动指定的值。要指定值,请将输入参量传递给绘图函数或直接设置YData属性。
z 坐标数据,指定为矩阵。
数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
极坐标数据
自 R2025a 起
角度值,指定为大小与 ZData 相同的矩阵或长度为 n 的向量,其中 [m,n] = size(ZData)。
此属性仅适用于极坐标图。
数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
自 R2025a 起
半径值,指定为大小与 ZData 相同的矩阵或长度为 m 的向量,其中 [m,n] = size(ZData)。
此属性仅适用于极坐标图。
数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | categorical | datetime | duration
颜色和透明度数据
顶点颜色,指定为下列形式之一:
2 维数组 - 使用颜色图颜色。通过将
CData设置为大小与ZData相同的数组来指定每个顶点的颜色。CDataMapping属性确定这些值如何映射到当前颜色图。如果FaceColor属性设置为'texturemap',则CData无需与ZData具有相同大小。但是,它必须为double或uint8类型。CData值映射到ZData定义的曲面。3 维数组 - 使用真彩色。通过将
CData设置为 m×n×3 数组(其中[m,n] = size(ZData))来为每个顶点指定一种 RGB 三元组颜色。RGB 三元组是三元素向量,用于指定颜色的红、绿和蓝分量的强度。数组的第一页包含颜色的红色分量,第二页包含颜色的绿色分量,第三页包含蓝色分量。由于曲面使用真彩色而不是颜色图颜色,因此CDataMapping属性没有任何作用。如果
CData为double或single类型,则 RGB 三元值[0 0 0]和[1 1 1]分别对应于黑色和白色。如果
CData为整数类型,则该曲面使用完整范围的数据以确定颜色。例如,如果CData为类型uint8,则[0 0 0]和[255 255 255]分别对应于黑色和白色。如果CData为类型int8,则[-128 -128 -128]和[127 127 127]分别对应于黑色和白色。
数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
CData 的选择模式,指定为下列值之一:
'auto'- 使用ZData值设置颜色。'manual'- 使用手动指定的值。要指定值,请设置CData属性。
直接或缩放颜色映射,指定为下列值之一:
scaled- 缩放颜色数据使其跨度覆盖坐标区的CLim属性指示的颜色图部分,以线性方式将数据值映射至颜色。direct- 使用颜色数据作为颜色图的直接索引。颜色数据应为介于 1 至length(colormap)范围内的整数值。MATLAB® 将小于 1 的值映射至颜色图中的第一种颜色,将大于length(colormap)的值映射至颜色图中的最后一种颜色。带小数部分的值舍取为最接近的整数。
每个顶点的透明度数据,指定为与 ZData 属性大小相同的数组。指定这些值后,请设置 FaceAlpha 和 EdgeAlpha 属性来控制透明度的类型。如果 FaceAlpha 和 EdgeAlpha 属性均设置为标量值,则 surface 不使用 AlphaData 值。
AlphaDataMapping 属性确定 surface 如何解释 AlphaData 属性值。
数据类型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
AlphaData 值的解释,指定为下列值之一:
'none'- 将值解释为透明度值。值 1 或更大的值表示完全不透明,值 0 或更小的值表示完全透明,介于 0 和 1 之间的值表示半透明。'scaled'- 将值映射到图窗的 alphamap 中。坐标区的最小和最大 alpha 范围确定分别映射到 alphamap 中第一个和最后一个元素的AlphaData值。例如,如果 alpha 范围是[3 5],则小于或等于3的值映射到 alphamap 中的第一个元素。大于或等于5的值映射到 alphamap 中的最后一个元素。坐标区的ALim属性包含 alpha 范围。图窗的Alphamap属性包含 alphamap。'direct'- 将值解释为图窗的 alphamap 的索引。带小数部分的值舍取为最接近的整数。如果值为
double或single类型,则小于或等于 1 的值将映射到 alphamap 中的第一个元素。等于或大于 alphamap 的长度的值映射到 alphamap 中的最后一个元素。如果值为整数类型,则小于或等于 0 的值将映射到 alphamap 中的第一个元素。等于或大于 alphamap 的长度的值映射到 alphamap 中的最后一个元素(或直到整数类型的最大值)。整数类型有
uint8、uint16、uint32、uint64、int8、int16、int32和int64。如果值为
logical类型,则值 0 将映射到 alphamap 中的第一个元素,值 1 将映射到 alphamap 中的第二个元素。
法线
每个曲面顶点的法向量,指定为 m×n×3 数组,其中 [m,n] = size(ZData)。为每个顶点指定一个法向量。
为此属性指定值会将关联的模式设置为手动模式。如果未指定法向量,则曲面生成这些数据以进行光照计算。
数据类型: single | double
VertexNormals 的选择模式,指定为下列值之一:
'auto'- 基于坐标数据计算法向量。'manual'- 使用手动指定的值。要指定值,请设置VertexNormals属性。
每个曲面的法向量,指定为 (m-1)×(n-1)×3 数组,其中 [m,n] = size(ZData)。为每个面指定一个法向量。
为此属性指定值会将关联的模式设置为手动模式。如果未指定法向量,则曲面生成这些数据以进行光照计算。
数据类型: single | double
FaceNormals 的选择模式,指定为下列值之一:
'auto'- 基于坐标数据计算法向量。'manual'- 使用手动指定的值。要指定值,请设置FaceNormals属性。
光照
环境光的强度,指定为范围 [0,1] 中的标量值。环境光是照亮整个场景的无方向性光源。在坐标区上必须至少有一个可见光对象才能使环境光成为可见的。
坐标区的 AmbientLightColor 属性设置环境光的颜色。坐标区中所有对象的颜色相同。
示例: 0.5
数据类型: double
散射光的强度,指定为范围 [0,1] 中的标量值。漫射光是来自坐标区中光源对象的非镜面反射光。
示例: 0.3
数据类型: double
镜面反射的强度,指定为范围 [0,1] 中的标量值。镜面反射是坐标区中光源对象射入曲面图形成的明亮点。
示例: 0.3
数据类型: double
镜面反射区的大小,指定为大于或等于 1 的标量值。大多数材料具有介于范围 [5 20] 内的指数。
示例: 7
数据类型: double
镜面反射的颜色,指定为范围 [0,1] 中的标量值。值为 1 时将使用光源的颜色设置颜色。值为 0 时将使用从其反射光的对象的颜色和光源的颜色设置对象的颜色。光的 Color 属性包含光源的颜色。对于介于这两个值之间的值,比例以线性方式变化。
示例: 0.5
数据类型: double
图例
图例标签,指定为字符向量或字符串标量。只有调用 legend 命令之后,才会显示图例。如果未指定文本,则 legend 使用 'dataN' 形式设置标签。
在图例中包含对象,指定为 Annotation 对象。将 Annotation 对象的基础 IconDisplayStyle 属性设置为以下值之一:
"on"- 在图例中包含对象(默认值)。"off"- 不在图例中包含对象。
例如,要从图例中排除名为 obj 的 Surface 对象,请将 IconDisplayStyle 属性设置为 "off"。
obj.Annotation.LegendInformation.IconDisplayStyle = "off";
您也可以使用 legend 函数控制图例中的项目。将第一个输入参量指定为要包含的图形对象的向量。如果未在第一个输入参量中指定现有图形对象,则该图形对象不会显示在图例中。但在创建图例后添加到坐标区的图形对象会显示在图例中。请考虑在创建所有绘图后创建图例以避免出现额外的项。
交互性
可见性状态,指定为 "on" 或 "off",或者指定为数值或逻辑值 1 (true) 或 0 (false)。值 "on" 等效于 true,"off" 等效于 false。因此,您可以使用此属性的值作为逻辑值。该值存储为 matlab.lang.OnOffSwitchState 类型的 on/off 逻辑值。
"on"- 显示对象。"off"- 隐藏对象而不删除它。您仍然可以访问不可见对象的属性。
数据提示内容,指定为 DataTipTemplate 对象。您可以通过修改底层 DataTipTemplate 对象的属性来控制数据提示中显示的内容。有关属性列表,请参阅 DataTipTemplate 属性。
有关修改数据提示的示例,请参阅创建自定义数据提示。
此属性仅适用于具有固定数据提示的曲面。
注意
findobj 或 findall 不返回 DataTipTemplate 对象,copyobj 也不复制该对象。
上下文菜单,指定为 ContextMenu 对象。使用此属性在您右键点击对象时显示上下文菜单。使用 uicontextmenu 函数创建上下文菜单。
注意
如果 PickableParts 属性设置为 'none' 或者 HitTest 属性设置为 'off',该上下文菜单将不显示。
选择状态,指定为 'on' 或 'off',或者指定为数值或逻辑值 1 (true) 或 0 (false)。值 'on' 等效于 true,'off' 等效于 false。因此,您可以使用此属性的值作为逻辑值。该值存储为 matlab.lang.OnOffSwitchState 类型的 on/off 逻辑值。
'on'- 已选择。如果您在绘图编辑模式下点击对象,则 MATLAB 会将其Selected属性设置为'on'。如果SelectionHighlight属性也设置为'on',则 MATLAB 将在对象周围显示选择句柄。'off'- 未选择。
选择时显示选择句柄,指定为 'on' 或 'off',或者指定为数值或逻辑值 1 (true) 或 0 (false)。值 'on' 等效于 true,'off' 等效于 false。因此,您可以使用此属性的值作为逻辑值。该值存储为 matlab.lang.OnOffSwitchState 类型的 on/off 逻辑值。
'on'- 在Selected属性设置为'on'时显示选择句柄。'off'- 永远不显示选择句柄,即使Selected属性设置为'on'也是如此。
按照坐标区范围裁剪对象,指定为 'on' 或 'off',或者指定为数值或逻辑值 1 (true) 或 0 (false)。值 'on' 等效于 true,'off' 等效于 false。因此,您可以使用此属性的值作为逻辑值。该值存储为 matlab.lang.OnOffSwitchState 类型的 on/off 逻辑值。
值为
'on'会裁剪对象超出坐标区范围的部分。值为
'off'会显示整个对象,即使对象的某些部分超出坐标区范围。如果您创建一个图、设置hold on、冻结坐标区缩放,然后创建比原始图更大的对象,则该对象的某些部分可能会显示在坐标区范围之外。
必须将包含该对象的坐标区的 Clipping 属性设置为 'on'。否则,此属性不起作用。有关裁剪行为的详细信息,请参阅坐标区的 Clipping 属性。
回调
鼠标点击回调,指定为下列值之一:
函数句柄
元胞数组,包含一个函数句柄和其他参量
作为有效 MATLAB 命令或函数(在基础工作区中计算)的字符向量(不推荐)
使用此属性在您点击对象时执行代码。如果使用函数句柄指定此属性,则 MATLAB 在执行回调时将向回调函数传递两个参量:
点击的对象 - 从回调函数中访问点击的对象的属性。
事件数据 - 空参量。在函数定义中将其替换为波浪号字符 (
~) 以指示不使用此参量。
有关如何使用函数句柄定义回调函数的详细信息,请参阅Create Callbacks for Graphics Objects。
注意
如果 PickableParts 属性设置为 'none' 或者 HitTest 属性设置为 'off',则不执行此回调。
对象创建函数,指定为下列值之一:
函数句柄。
第一个元素是函数句柄的元胞数组。元胞数组中的后续元素是传递到回调函数的参量。
包含有效 MATLAB 表达式的字符向量(不推荐)。MATLAB 在基础工作区计算此表达式。
有关将回调指定为函数句柄、元胞数组或字符向量的详细信息,请参阅Create Callbacks for Graphics Objects。
此属性指定要在 MATLAB 创建对象时执行的回调函数。MATLAB 将在执行 CreateFcn 回调之前初始化所有属性值。如果不指定 CreateFcn 属性,则 MATLAB 执行默认的创建函数。
对现有组件设置 CreateFcn 属性没有任何作用。
如果将此属性指定为函数句柄或元胞数组,则可以使用回调函数的第一个参量访问正在创建的对象。否则,使用 gcbo 函数访问该对象。
对象删除函数,指定为下列值之一:
函数句柄。
第一个元素是函数句柄的元胞数组。元胞数组中的后续元素是传递到回调函数的参量。
包含有效 MATLAB 表达式的字符向量(不推荐)。MATLAB 在基础工作区计算此表达式。
有关将回调指定为函数句柄、元胞数组或字符向量的详细信息,请参阅Create Callbacks for Graphics Objects。
此属性指定在 MATLAB 删除对象时要执行的回调函数。MATLAB 在销毁对象的属性之前执行 DeleteFcn 回调。如果不指定 DeleteFcn 属性,则 MATLAB 执行默认的删除函数。
如果将此属性指定为函数句柄或元胞数组,则可以使用回调函数的第一个参量访问要删除的对象。否则,使用 gcbo 函数访问该对象。
回调执行控件
回调中断,指定为 'on' 或 'off',或者指定为数值或逻辑值 1 (true) 或 0 (false)。值 'on' 等效于 true,'off' 等效于 false。因此,您可以使用此属性的值作为逻辑值。该值存储为 matlab.lang.OnOffSwitchState 类型的 on/off 逻辑值。
此属性确定是否可以中断运行中回调。有以下两种回调状态要考虑:
运行中回调是当前正在执行的回调。
中断回调是试图中断运行中回调的回调。
每次执行处理回调队列的命令时,MATLAB 都会确定回调中断行为。这些命令包括 drawnow、figure、uifigure、getframe、waitfor 和 pause。
如果运行中回调不包含上述命令之一,则不会发生中断。MATLAB 首先完成执行运行中回调,然后执行中断回调。
如果运行中回调确实包含上述命令之一,则由运行中回调所属对象的 Interruptible 属性来确定是否发生中断:
如果
Interruptible的值为'off',则不会发生中断。此时,由中断回调所属对象的BusyAction属性确定中断回调是被丢弃还是添加到回调队列中。如果
Interruptible的值为'on',则发生中断。下次 MATLAB 处理回调队列时,它会停止运行中回调的执行,并执行中断回调。在中断回调完成后,MATLAB 将继续执行运行中回调。
注意
回调的中断和执行在以下情况下会有不同的表现:
如果中断回调是
DeleteFcn、CloseRequestFcn或SizeChangedFcn回调,则无论是否存在Interruptible属性值都会发生中断。如果运行中回调当前正在执行
waitfor函数,则无论是否存在Interruptible属性值都会发生中断。如果中断回调由
Timer对象所有,则回调将根据调度执行,而不考虑Interruptible属性值。
回调排队,指定为 'queue' 或 'cancel'。BusyAction 属性决定 MATLAB 如何处理中断回调的执行。有以下两种回调状态要考虑:
运行中回调是当前正在执行的回调。
中断回调是试图中断运行中回调的回调。
BusyAction 属性仅在同时满足以下两个条件时才确定回调排队行为:
在这些情况下,由中断回调所属对象的 BusyAction 属性确定 MATLAB 如何处理中断回调。以下是 BusyAction 属性的可能值:
'queue'- 将中断回调放入队列中,以便在运行中回调执行完毕后进行处理。'cancel'- 不执行中断回调。
捕获鼠标点击的能力,指定为以下值之一:
'visible'- 当对象可见时,捕获鼠标点击。Visible属性必须设置为'on',而且您必须点击Surface对象中具有定义颜色的部分。不能点击包含设置为'none'的相关颜色属性的部分。如果绘图包含标记,当边或填充区具有定义的颜色时,则整个标记都是可点击的。HitTest属性决定是Surface对象响应点击还是前代响应点击。'all'- 无论是否可见都捕获鼠标点击。Visible属性可以设置为'on'或'off',而且您可以点击Surface对象中没有颜色的部分。HitTest属性决定是Surface对象响应点击还是前代响应点击。'none'- 无法捕获鼠标点击。点击Surface对象会将点击操作通过它传递给图窗窗口当前视图中该对象下方的对象。HitTest属性没有任何作用。
对捕获的鼠标点击的响应,指定为 'on' 或 'off',或者指定为数值或逻辑值 1 (true) 或 0 (false)。值 'on' 等效于 true,'off' 等效于 false。因此,您可以使用此属性的值作为逻辑值。该值存储为 matlab.lang.OnOffSwitchState 类型的 on/off 逻辑值。
'on'- 触发Surface对象的ButtonDownFcn回调。如果您已定义ContextMenu属性,则调用上下文菜单。'off'- 触发满足以下条件之一的Surface对象的最近前代的回调:HitTest属性设置为'on'。PickableParts属性设置为允许前代捕获鼠标点击的值。
注意
PickableParts 属性决定 Surface 对象是否可以捕获鼠标点击。如果无法捕获,则 HitTest 属性没有任何作用。
此 属性 为只读。
删除状态,以 matlab.lang.OnOffSwitchState 类型的 on/off 逻辑值形式返回。
当 DeleteFcn 回调开始执行时,MATLAB 会将 BeingDeleted 属性设置为 'on'。BeingDeleted 属性将一直保持 'on' 设置状态,直到组件对象不再存在为止。
在查询或修改对象之前,请先检查其 BeingDeleted 属性的值,以确认它不是待删除项。
父级/子级
父级,指定为 Axes、PolarAxes、Group 或 Transform 对象。
子级,以空的 GraphicsPlaceholder 数组或 DataTip 对象数组形式返回。使用此属性来查看在图上绘制的数据提示的列表。
不能使用 Children 属性添加或删除子级。要向此列表中添加子级,请将 DataTip 对象的 Parent 属性设置为图对象。
父级的 Children 属性中对象句柄的可见性,指定为下列值之一:
"on"- 对象句柄始终可见。"off"- 对象句柄始终不可见。该选项用于防止另一函数无意中对其进行更改。将HandleVisibility设置为"off"可在执行该函数时暂时隐藏句柄。"callback"- 对象句柄在回调或回调所调用的函数中可见,但在从命令行调用的函数中不可见。此选项阻止通过命令行访问对象,但允许回调函数访问对象。
如果父级的 Children 属性中未列出该对象,则通过搜索对象层次结构或查询句柄属性获取对象句柄的函数无法返回该对象。此类函数的示例包括 get、findobj、gca、gcf、gco、newplot、cla、clf 和 close 函数。
隐藏的对象句柄仍有效。将根 ShowHiddenHandles 属性设置为 "on" 以列出所有对象句柄,而不管其 HandleVisibility 属性设置如何。
标识符
此 属性 为只读。
图形对象的类型,返回 'surface'
对象标识符,指定为字符向量或字符串标量。您可以指定唯一的 Tag 值作为对象的标识符。如果需要访问您代码中其他位置的对象,可以使用 findobj 函数基于 Tag 值搜索对象。
用户数据,指定为任何 MATLAB 数组。例如,您可以指定标量、向量、矩阵、元胞数组、字符数组、表或结构体。使用此属性存储对象上的任意数据。
如果您在 App 设计工具中工作,请在该 App 中创建公共或私有属性以共享数据,而不是使用 UserData 属性。有关详细信息,请参阅在用 App 设计工具创建的 App 内共享数据。
版本历史记录
在 R2006a 之前推出MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)