odeJacobian

ODE Jacobian matrix

Since R2023b

Description

An odeJacobian object represents the Jacobian matrix for a system of ordinary differential equations. The Jacobian is a matrix of partial derivatives of the functions in the system of differential equations.

$J = \frac{\partial f}{\partial y} = [\begin{matrix} \frac{\partial f_{1}}{\partial y_{1}} & \frac{\partial f_{1}}{\partial y_{2}} & \dots \\ \frac{\partial f_{2}}{\partial y_{1}} & \frac{\partial f_{2}}{\partial y_{2}} & \dots \\ ⋮ & ⋮ \end{matrix}]$

Create an ode object to represent the ODE problem, and specify an odeJacobian object as the value of the Jacobian property to incorporate a Jacobian matrix or its sparsity pattern into the problem.

Creation

Syntax

J = odeJacobian

J = odeJacobian(PropertyName=Value)

Description

J = odeJacobian creates an odeJacobian object with empty properties.

J = odeJacobian(PropertyName=Value) specifies one or more property values using name-value arguments. For example, J = odeJacobian(Jacobian=[0 1; -2 1]) specifies a constant Jacobian matrix.

example

Properties

expand all

`Jacobian` — Jacobian matrix
matrix | cell array | function handle

Jacobian matrix, specified as a matrix, cell array, or handle to a function that evaluates the Jacobian. The Jacobian is a matrix of partial derivatives of the functions that define the system of differential equations.

For stiff ODE solvers (ode15s, ode23s, ode23t, and ode23tb), providing information about the Jacobian matrix is critical for reliability and efficiency. If you do not provide the Jacobian, then the ODE solver approximates it numerically using finite differences.

For large systems of equations where it is not feasible to provide the entire analytic Jacobian, use the SparsityPattern property to pass in the sparsity pattern of the Jacobian matrix. The solver uses the sparsity pattern to calculate a sparse Jacobian.

You can specify the Jacobian property as:

A constant matrix with calculated values for $\frac{\partial f}{\partial y}$ .
When EquationType is "fullyimplicit", a two-element cell array with calculated values for the constant Jacobian with respect to y in the first element and yp in the second element. If you specify one of the elements as [], the ODE solver approximates the corresponding Jacobian numerically while taking the provided values in the other element into account. (since R2024b)
A handle to a function that computes the matrix elements and that accepts two input arguments, dfdy = Fjac(t,y). To give the function access to parameter values in the Parameters property, specify a third input argument in the function definition, dfdy = Fjac(t,y,p).
When EquationType is "fullyimplicit", a handle to a function that computes the matrix elements and that accepts three input arguments, [dfdy,dfdp] = Fjac(t,y,yp). To give the function access to parameter values in the Parameters property, specify a fourth input argument in the function definition, [dfdy,dfdp] = Fjac(t,y,yp,p). (since R2024b)

Example: J = odeJacobian(Jacobian=@Fjac) specifies the function Fjac that evaluates the Jacobian matrix.

Example: J = odeJacobian(Jacobian=[0 1; -2 1]) specifies a constant Jacobian matrix.

Data Types: single | double | cell | function_handle

`SparsityPattern` — Jacobian sparsity pattern
sparse matrix | cell array

Jacobian sparsity pattern, specified as a sparse matrix or cell array. The sparse matrix contains 1s where there might be nonzero entries in the Jacobian. The ODE solver uses the sparsity pattern to generate a sparse Jacobian matrix numerically. Use this property to improve execution time when the ODE system is large, sparse, and you cannot provide an analytic Jacobian.

If the EquationType property of the ode object is "fullyimplicit", specify a constant sparsity pattern as a cell array where the first element is the sparsity pattern for the Jacobian with respect to y and the second element is the sparsity pattern for the Jacobian with respect to yp. If you specify one of the elements of the cell array as [], the ODE solver approximates the corresponding Jacobian numerically while taking the provided values in the other element into account.

Note

If you specify a Jacobian matrix using the Jacobian property, then the solver ignores the SparsityPattern property.

Example: J = odeJacobian(SparsityPattern=S) specifies the Jacobian sparsity pattern using sparse matrix S.

Data Types: single | double | cell (since R2024b)

Examples

collapse all

Specify Jacobian Matrix for Stiff ODE

Open Live Script

The Van der Pol oscillator equation is a second-order differential equation. The equation includes a parameter $μ$ , and the equation becomes stiff when the value of $μ$ is large.

$\frac{d^{2} x}{d t^{2}} - μ (1 - x^{2}) \frac{d x}{d t} + x = 0$

Using the substitutions $y_{1} = x$ and $y_{2} = \frac{dx}{dt}$ produces a system of two first-order equations.

$\begin{array}{l} \frac{d y_{1}}{d t} = y_{2} \\ \frac{d y_{2}}{d t} = μ (1 - y_{1}^{2}) y_{2} - y_{1} \end{array}$

The Jacobian matrix for these equations is the matrix of partial derivatives of each equation with respect to both $y_{1}$ and $y_{2}$ .

$J = [\begin{array}{ccc} \frac{\partial f_{1}}{\partial y_{1}} & \frac{\partial f_{1}}{\partial y_{2}} \\ \frac{\partial f_{2}}{\partial y_{1}} & \frac{\partial f_{2}}{\partial y_{2}} \end{array}] = [\begin{array}{ccc} 0 & 1 \\ - 2 μ y_{1} y_{2} - 1 & μ (1 - y_{1}^{2}) \end{array}]$

Solve the Van der Pol oscillator using $μ = 1000$ and initial values of [2; 0] by creating an ode object to represent the problem.

Store the value of $μ$ in the Parameters property.
Specify the initial values in the InitialValue property.
Specify the system of equations in the ODEFcn property, specifying three input arguments so that the value for $μ$ is passed to the function.
Specify a function that calculates the Jacobian matrix in the Jacobian property, specifying three input arguments so that the value for $μ$ is passed to the function.

F = ode;
F.Parameters = 1000;
F.InitialValue = [2; 0];
F.ODEFcn = @(t,y,p) [y(2); p(1)*(1-y(1)^2)*y(2)-y(1)];
F.Jacobian = @(t,y,p) [0 1; -2*p(1)*y(1)*y(2)-1  p(1)*(1-y(1)^2)];

Display the ode object. The SelectedSolver property shows that the ode15s solver was automatically chosen for this problem.

F = 
  ode with properties:

   Problem definition
               ODEFcn: @(t,y,p)[y(2);p(1)*(1-y(1)^2)*y(2)-y(1)]
           Parameters: 1000
          InitialTime: 0
         InitialValue: [2×1 double]
             Jacobian: [1×1 odeJacobian]
         EquationType: standard

   Solver properties
    AbsoluteTolerance: 1.0000e-06
    RelativeTolerance: 1.0000e-03
               Solver: auto
       SelectedSolver: ode15s

  Show all properties

Solve the system of equations over the time interval [0 3000] by using the solve method. Plot the first solution component.

S = solve(F,0,3000);
plot(S.Time,S.Solution(1,:),"-o")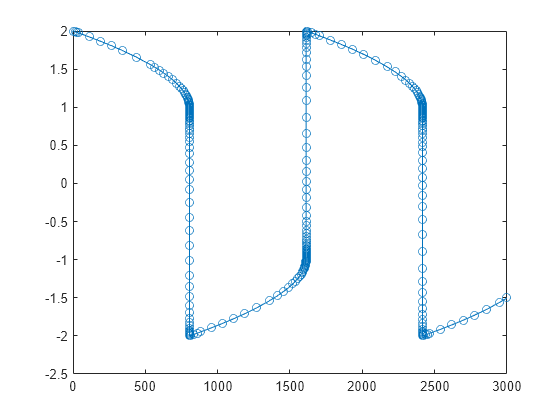

Figure contains an axes object. The axes object contains an object of type line.

Version History

Introduced in R2023b

expand all

R2025a: Specify single-precision property values

You can specify the Jacobian matrix Jacobian and sparsity pattern SparsityPattern as single-precision sparse matrices. You can also specify Jacobian as a function handle that returns single-precision outputs.

R2024b: Specify Jacobian for implicit ODEs

The Jacobian property can accept functions of the form dfdy = Fjac(t,y,yp) for implicit ODEs. Specify the ode object property EquationType as "fullyimplicit" to use the three-argument form for Jacobian.

If EquationType is "fullyimplicit", the Jacobian and SparsityPattern properties also accept a two-element cell array, where the first element corresponds to the Jacobian with respect to y and the second element corresponds to the Jacobian with respect to yp.

odeJacobian

Description

Creation

Syntax

Description

Properties

Jacobian — Jacobian matrix matrix | cell array | function handle

SparsityPattern — Jacobian sparsity pattern sparse matrix | cell array

Examples

Specify Jacobian Matrix for Stiff ODE

Version History

R2025a: Specify single-precision property values

R2024b: Specify Jacobian for implicit ODEs

See Also

`Jacobian` — Jacobian matrix
matrix | cell array | function handle

`SparsityPattern` — Jacobian sparsity pattern
sparse matrix | cell array