slerp
Spherical linear interpolation
Description
Examples
Input Arguments
Output Arguments
Algorithms
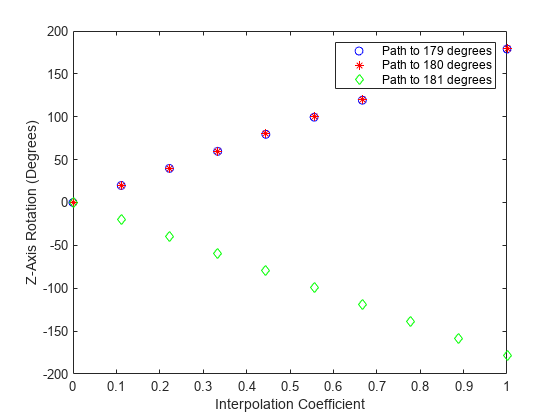
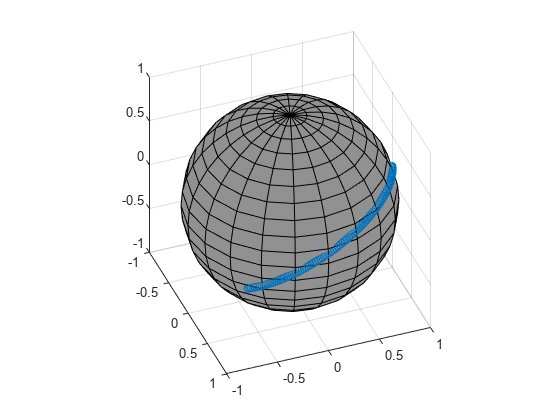
Quaternion spherical linear interpolation (SLERP) is an extension of linear interpolation along a plane to spherical interpolation in three dimensions. The algorithm was first proposed in [1]. Given two quaternions, q1 and q2, SLERP interpolates a new quaternion, q0, along the great circle that connects q1 and q2. The interpolation coefficient, T, determines how close the output quaternion is to either q1 and q2.
The SLERP algorithm can be described in terms of sinusoids:
where q1 and q2 are normalized quaternions, and θ is half the angular distance between q1 and q2.
References
[1] Shoemake, Ken. "Animating Rotation with Quaternion Curves." ACM SIGGRAPH Computer Graphics 19, no. 3 (July 1985): 245–54. https://doi.org/10.1145/325165.325242.