Benchmark Path Planners for Differential Drive Robots in Warehouse Map

map = load("wareHouseMap.mat").logicalMap;
map = binaryOccupancyMap(map);

figure
show(map)
title("Warehouse Floor Plan")

% Set the location of text displayed on the map.
loadingStationTextLoc = [40 9 0];
unloadingStationTextLoc = [7.5 42 0];
hold on
text(loadingStationTextLoc(1),loadingStationTextLoc(2),1,"Loading Station");
text(unloadingStationTextLoc(1),unloadingStationTextLoc(2),1,"Unloading Stations");
hold off

minTurningRadius = 1.4; % In meters.

stateSpace = stateSpaceDubins([map.XWorldLimits; map.YWorldLimits; [-pi pi]]);
stateSpace.MinTurningRadius = minTurningRadius;

validator = validatorOccupancyMap(stateSpace,Map=map);
validator.ValidationDistance = 0.01*(1/map.Resolution); % In meters.

rrtInit = @(validator) plannerRRTWrapper(validator);
rrtStarInit = @(validator) plannerRRTStarWrapper(validator);
birrtInit = @(validator) plannerBiRRTWrapper(validator);
haStarInit = @(validator) plannerHybridAStarWrapper(validator,minTurningRadius);
prmInit = @(validator) plannerPRM(validator.StateSpace,validator,MaxNumNodes=80);

planFcn = @(initOutput,start,goal) plan(initOutput,start,goal);

% Set default random number for repeatability of results.
rng("default")

% Select the number of start-goal pairs.
numStartGoalPairs = 3;

loadingArea = [51.5 11 5 10];
startLocations = helperSampleSelectedAreaOnMap(validator,loadingArea,numStartGoalPairs);

unloadingArea = [2 43.5 27 15];
goalLocations = helperSampleSelectedAreaOnMap(validator,unloadingArea,numStartGoalPairs);

show(map)
title("Warehouse Floor Plan")

% Indicate the loading and unloading station on the map.
hold on
text(loadingStationTextLoc(1),loadingStationTextLoc(2),1,"Loading Station");
rectangle(Position=loadingArea)
text(unloadingStationTextLoc(1),unloadingStationTextLoc(2),1,"Unloading Stations");
rectangle(Position=unloadingArea)

% Set the length of the line representing the pose in the start-goal visualization.
r = 2;

% Display all the start-goal pairs on the map.
for i=1:numStartGoalPairs
    start = startLocations(i,:);
    goal = goalLocations(i,:);    
    
    % Define the legend displayed on the map.    
    startString = strcat("start location",num2str(i));
    goalString = strcat("goal location",num2str(i));
    
    % Display start and goal location of robot.
    p1 = plot(start(1,1),start(1,2),"o",DisplayName=startString);
    c1 = p1.Color;
    p2 = plot(goal(1,1),goal(1,2),"o",DisplayName=goalString);
    c2 = p2.Color;
    
    % Display start and goal headings.
    plot([start(1) start(1)+r*cos(start(3))],[start(2) start(2)+r*sin(start(3))],...
         "-",Color=c1,HandleVisibility="off")
    plot([goal(1) goal(1)+r*cos(goal(3))],[goal(2) goal(2)+r*sin(goal(3))],...
         "-",Color=c2,HandleVisibility="off")       
end
hold off
legend(Location="northeastoutside")

% To store the generated benchmark objects for each start-goal pair.
benchmarkList = cell(1,numStartGoalPairs);

% Specify the number of times each planner to be executed on the same
% set of start-goal pair.
runCount = 2;
for i=1:size(startLocations,1)
    
    % Get each start and goal location from all the sampled locations.
    start = startLocations(i,:);
    goal = goalLocations(i,:);
    
    % Set default random number for repeatability of results.
    rng("default")

    % Construct benchmark object.
    benchmark = plannerBenchmark(validator,start,goal);
    
    % Add planners for benchmarking using initialization and plan function
    % handles. Additional optional input NumPlanOutput define the number of
    % outputs returned from the plan function.
    addPlanner(benchmark,planFcn,rrtInit,PlannerName="rrt",NumPlanOutput=2)
    addPlanner(benchmark,planFcn,rrtStarInit,PlannerName="rrtStar",NumPlanOutput=2)
    addPlanner(benchmark,planFcn,birrtInit,PlannerName="biRRT",NumPlanOutput=2)
    addPlanner(benchmark,planFcn,prmInit,PlannerName="PRM",NumPlanOutput=2)
    addPlanner(benchmark,planFcn,haStarInit,PlannerName="hybridAstar",NumPlanOutput=2)    
    
    % Run the benchmark.
    runPlanner(benchmark,runCount)

    % Store the benchmark for further analysis.
    benchmarkList{i} = benchmark;
end

helperPlotAveragedMetrics(benchmarkList,runCount,"clearance")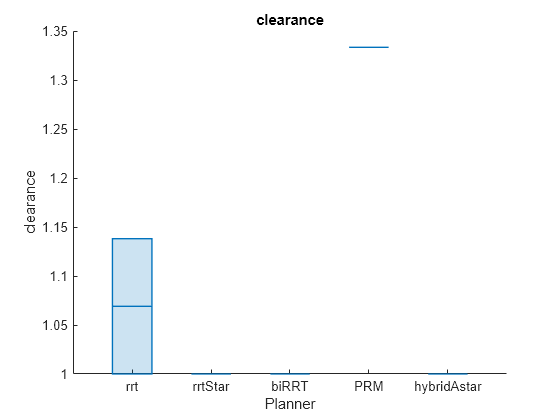

clearanceAverage = helperCalculateAverageMetricTable(benchmarkList,"clearance")

helperPlotAveragedMetrics(benchmarkList,runCount,"isPathValid")

isPathValidAverage = helperCalculateAverageMetricTable(benchmarkList,"isPathValid")

helperPlotAveragedMetrics(benchmarkList,runCount,"executionTime")

execTimeAverage = helperCalculateAverageMetricTable(benchmarkList,"executionTime")

helperPlotAveragedMetrics(benchmarkList,runCount,"initializationTime")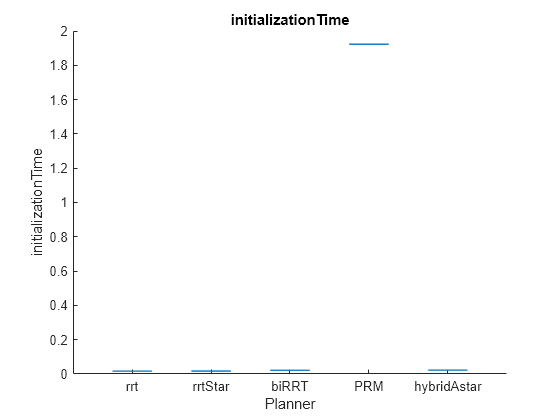

initTimeAverage = helperCalculateAverageMetricTable(benchmarkList,"initializationTime")

helperPlotAveragedMetrics(benchmarkList,runCount,"pathLength")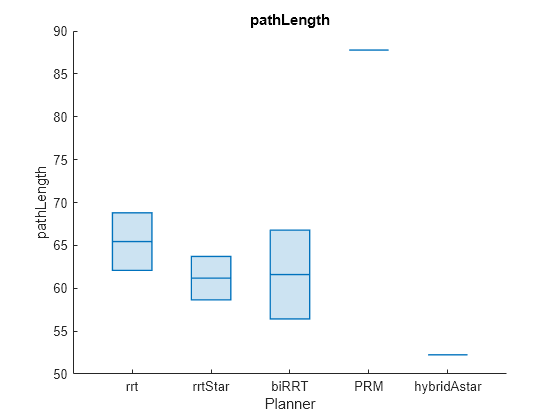

pathLengthAverage = helperCalculateAverageMetricTable(benchmarkList,"pathLength")

helperPlotAveragedMetrics(benchmarkList,runCount,"smoothness")

smoothnessAverage = helperCalculateAverageMetricTable(benchmarkList,"smoothness")

pathLengthMean = zeros(1,numStartGoalPairs);

% Iterate over all the benchmarks and store the mean path length for each
% start-goal pair.
for i=1:numStartGoalPairs
    benchmark = benchmarkList{i};
    pathLengthTable= benchmark.metric("pathLength");
    pathLengthMean(i) = pathLengthTable.Mean("biRRT"); 
end

% Find the index of the benchmark which produced largest mean path length
% value for plannerBiRRT.
[~,largestPathLengthIdx] = max(pathLengthMean);
benchmarkLargestPathlength = benchmarkList{largestPathLengthIdx};
show(benchmarkLargestPathlength,"pathLength")

pathLength = metric(benchmarkLargestPathlength,"pathLength")

% Retrieve the start and goal location from the benchmark object.
start = benchmarkLargestPathlength.Start;
goal = benchmarkLargestPathlength.Goal;

% Display the path from start location to goal location for all the path
% planners for all the runs in runCount.
for run=1:runCount
    figure
    show(map)
    title(['Path output from all planners for Run ' num2str(run)])
    hold on
    
    % Show start and goal positions of robot.
    plot(start(1,1),start(1,2),"o")
    plot(goal(1,1),goal(1,2),"o")
    
    % Find the planner names used for benchmarking.
    plannerNames = fieldnames(benchmarkLargestPathlength.PlannerOutput);
    numPlanners = length(plannerNames);
    runString = strcat("Run",num2str(run));
    
    % Iterate and plot path of each planner for the specified run.
    for i=1:numPlanners
        plannerName = plannerNames{i};
        plannerOutput = benchmarkLargestPathlength.PlannerOutput.(plannerName).PlanOutput.(runString);
        pathObj = plannerOutput{1};
        
        % Insert more states in the path to visualize the dubins curve. 
        interpolate(pathObj,200);
        plot(pathObj.States(:,1),pathObj.States(:,2),"-","LineWidth",2)
    end
    
    % Specify the legends.
    labels = [{"start location","goal location"} plannerNames'];
    legend(labels,location="northeastoutside")  
    hold off
end

planFcnWithShorten = @(initOutput,start,goal) planWithShorten(initOutput,start,goal);

% To store the generated benchmark objects for each start-goal pair.
rrtBenchmarkList = cell(1,numStartGoalPairs);

% Specify the number of times each planner to be executed on the same
% set of start-goal pair.
rrtRunCount = 2;

for i=1:height(startLocations)
    
    % Get each start and goal location from all the sampled locations.
    start = startLocations(i,:);
    goal = goalLocations(i,:);

    % Construct benchmark object.
    benchmark = plannerBenchmark(validator,start,goal);
    
    % Add planners for benchmarking using initialization and plan function
    % handles. Additional optional input NumPlanOutput define the number of
    % outputs returned from the plan function.
    addPlanner(benchmark,planFcnWithShorten,rrtInit,PlannerName="rrtWithShorten",NumPlanOutput=2)
    addPlanner(benchmark,planFcn,rrtStarInit,PlannerName="rrtStar",NumPlanOutput=2)
    
    % Run the benchmark.
    runPlanner(benchmark,rrtRunCount, Verbose="off")

    % Store the benchmark for further analysis.
    rrtBenchmarkList{i} = benchmark;
end

helperPlotAveragedMetrics(rrtBenchmarkList,rrtRunCount,"pathLength")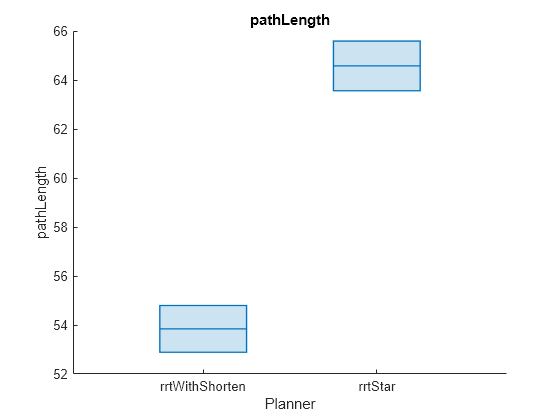

rrtClearanceAvg = helperCalculateAverageMetricTable(rrtBenchmarkList,"pathLength")

helperPlotAveragedMetrics(rrtBenchmarkList,rrtRunCount,"executionTime")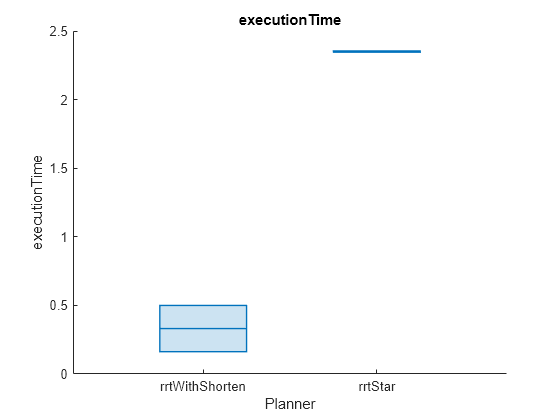

rrtExecTimeAvg = helperCalculateAverageMetricTable(rrtBenchmarkList,"executionTime") 

helperPlotAveragedMetrics(rrtBenchmarkList,rrtRunCount,"smoothness")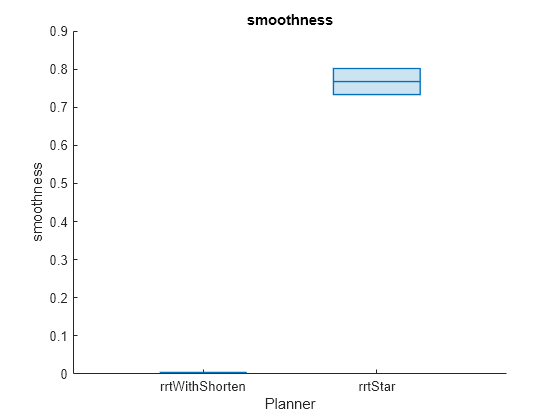

rrtSmoothnessAvg = helperCalculateAverageMetricTable(rrtBenchmarkList,"smoothness")

function planner = plannerHybridAStarWrapper(validator,minTurningRadius)
    map = validator.Map;
    ss = stateSpaceSE2;
    sv = validatorOccupancyMap(ss,Map=map);
    sv.ValidationDistance = validator.ValidationDistance;
    planner = plannerHybridAStar(sv,MinTurningRadius=minTurningRadius);
end

function planner = plannerBiRRTWrapper(sv)
    planner = plannerBiRRT(sv.StateSpace,sv);
    planner.EnableConnectHeuristic = true;
    planner.MaxIterations = 5e4;
    planner.MaxNumTreeNodes = 5e4;
    planner.MaxConnectionDistance = 5;
end

function planner = plannerRRTStarWrapper(sv)
    planner = plannerRRTStar(sv.StateSpace,sv);
    planner.MaxIterations = 2.5e3;
    planner.MaxNumTreeNodes = 2.5e3;
    planner.MaxConnectionDistance = 3;
    planner.ContinueAfterGoalReached = true;
end

function planner = plannerRRTWrapper(sv)
    planner = plannerRRT(sv.StateSpace,sv);
    planner.MaxIterations = 2.5e3;
    planner.MaxNumTreeNodes = 2.5e3;
    planner.MaxConnectionDistance = 3;
end

function [shortenedPath,solnInfo] = planWithShorten(planner, start, goal)
    [path,solnInfo] = plan(planner, start, goal);
    shortenedPath = shortenpath(path, planner.StateValidator);
end