使用基于求解器的锥规划最小化分段线性质量-弹簧系统的能量
此示例显示如何找到悬挂在两个锚点的质量-弹簧系统的平衡位置。弹簧具有分段线性拉力。该系统由二维空间中的 个质量组成。质量 与弹簧 和 相连。弹簧 和 也连接到单独的锚点。在这种情况下,弹簧 的零力长度为正长度 ,并且弹簧在拉伸到长度 时会产生力 。问题在于找到质量的最小势能配置,其中势能来自重力和非线性弹簧的拉伸。平衡发生在最小能量配置上。
该图显示了五个弹簧和四个质量悬挂在两个锚点上。
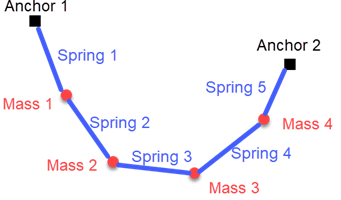
质量 在高度 处的势能为 ,其中 是地球引力常数。另外,弹簧常数为 的理想线性弹簧拉伸至长度 时,其势能为 。当前的模型是弹簧不是理想的,但具有非零的静止长度 。
本例的数学基础来自 Lobo、Vandenberg、Boyd 和 Lebret [1]。有关此示例的基于问题的版本,请参阅 基于问题的锥规划最小化分段线性质量-弹簧系统的能量。
数学表示
质量 的位置为 ,水平坐标为 ,垂直坐标为 。质量 由于 的重力而具有势能。弹簧 中的势能为 ,其中 是质量 和质量 之间的弹簧长度。以锚点 1 作为质量 0 的位置,以锚点 2 作为质量 的位置。前面的能量计算表明,弹簧 的势能为
.
将此势能问题重新表述为二阶锥问题需要引入一些新变量,如 Lobo [1] 中所述。创建等于项 的平方根的变量 。
令 为单位列向量 。则 。问题变成了
(1)
现在将 视为一个自由向量变量,不是由前面的 方程给出的。将 和 之间的关系纳入新的锥约束
(2)
目标函数在其变量中还不是线性的,正如 coneprog 所要求的那样。引入一个新的标量变量 。请注意,不等式 等价于不等式
.(3)
现在的问题是最小化
(4)
受制于 (2) 中列出的 和 的锥约束以及 (3) 的附加锥约束。锥约束 (3) 确保 。因此,问题(4)等价于问题(1)。
问题 (4) 中的目标函数和锥约束适合用 coneprog 解。
MATLAB® 表示
定义六个弹簧常数 、六个长度常数 和五个质量 。
k = 40*(1:6); l = [1 1/2 1 2 1 1/2]; m = [2 1 3 2 1];
定义地球上的近似引力常数 。
g = 9.807;
需要优化的变量是 向量的十个分量、 向量的六个分量以及 变量。让 v 成为包含所有这些变量的向量。
[v(1),v(2)]对应于二维变量 。[v(3),v(4)]对应于二维变量 。[v(5),v(6)]对应于二维变量 。[v(7),v(8)]对应于二维变量 。[v(9),v(10)]对应于二维变量 。[v(11):v(16)]对应于 6 维向量 。v(17)对应于标量变量 。
使用这些变量,创建相应的目标函数向量 f。
f = zeros(size(m)); f = [f;g*m]; f = f(:); f = [f;zeros(length(k)+1,1)]; f(end) = 1;
创建与质量之间的弹簧相对应的锥约束(2)
.
coneprog 求解器使用锥约束来求解变量向量 ,形式如下
.
在下面的代码中,Asc 矩阵代表项 ,其中 bsc = [0;0]。锥变量 dsc = 以及对应的 gamma =
d = zeros(1,length(f)); Asc = d; Asc([1 3]) = [1 -1]; A2 = circshift(Asc,1); Asc = [Asc;A2]; ml = length(m); dbase = 2*ml; bsc = [0;0]; for i = 2:ml gamma = -l(i); dsc = d; dsc(dbase + i) = sqrt(2/k(i)); conecons(i) = secondordercone(Asc,bsc,dsc,gamma); Asc = circshift(Asc,2,2); end
通过使用锚点作为末端质量的位置,创建与末端质量和锚点之间的弹簧相对应的锥约束,如前面的代码所示。
x0 = [0;5]; xn = [5;4]; Asc = zeros(size(Asc)); Asc(1,(dbase-1)) = 1; Asc(2,dbase) = 1; bsc = xn; gamma = -l(ml); dsc = d; dsc(dbase + ml) = sqrt(2/k(ml)); conecons(ml + 1) = secondordercone(Asc,bsc,dsc,gamma); Asc = zeros(size(Asc)); Asc(1,1) = 1; Asc(2,2) = 1; bsc = x0; gamma = -l(1); dsc = d; dsc(dbase + 1) = sqrt(2/k(1)); conecons(1) = secondordercone(Asc,bsc,dsc,gamma);
创建与 变量对应的锥约束(3)
通过创建矩阵 Asc,将其与 v 向量相乘,得到向量 。bsc 向量对应于项 中的常数 1。dsc 向量与 v 相乘后返回 。并且 gamma = 。
Asc = 2*eye(length(f)); Asc(1:dbase,:) = []; Asc(end,end) = -1; bsc = zeros(size(Asc,1),1); bsc(end) = -1; dsc = d; dsc(end) = 1; gamma = -1; conecons(ml+2) = secondordercone(Asc,bsc,dsc,gamma);
最后,创建与 和 变量对应的下界。
lb = -inf(size(f)); lb(dbase+1:end) = 0;
求解问题并绘制解
问题表示已完成。通过调用 coneprog 求解问题。
[v,fval,exitflag,output] = coneprog(f,conecons,[],[],[],[],lb);
Optimal solution found.
绘制解点和锚点。
pp = v(1:2*ml); pp = reshape(pp,2,[]); pp = pp'; plot(pp(:,1),pp(:,2),'ro') hold on xx = [x0,xn]'; plot(xx(:,1),xx(:,2),'ks') xlim([x0(1)-0.5,xn(1)+0.5]) ylim([min(pp(:,2))-0.5,max(x0(2),xn(2))+0.5]) xxx = [x0';pp;xn']; plot(xxx(:,1),xxx(:,2),'b--') legend('Calculated points','Anchor points','Springs','Location',"best") hold off

您可以更改参数 m、l 和 k 的值,看看它们如何影响解。您还可以改变质量数;代码会从您提供的数据中获取质量数。
参考资料
[1] Lobo, Miguel Sousa, Lieven Vandenberghe, Stephen Boyd, and Hervé Lebret.“Applications of Second-Order Cone Programming.”Linear Algebra and Its Applications 284, no. 1–3 (November 1998):193–228. https://doi.org/10.1016/S0024-3795(98)10032-0.