基于问题的锥规划最小化分段线性质量-弹簧系统的能量

打开实时脚本

此示例说明如何使用基于问题的方法来找到悬挂在两个锚点上的质量-弹簧系统的平衡位置。弹簧具有分段线性拉力。该系统由二维空间中的 $n$ 个质量组成。质量 $i$ 与弹簧 $i$ 和 $i + 1$ 相连。弹簧 $1$ 和 $n + 1$ 也连接到单独的锚点。在这种情况下，弹簧 $i$ 的零力长度为正长度 $l (i)$ ，并且弹簧在拉伸到长度 $q + l (i)$ 时会产生力 $k (i) q$ 。问题在于找到质量的最小势能配置，其中势能来自重力和非线性弹簧的拉伸。平衡发生在最小能量配置上。

该图显示了五个弹簧和四个质量悬挂在两个锚点上。

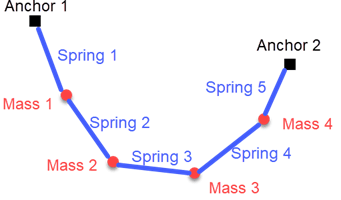
质量 $m$ 在高度 $h$ 处的势能为 $m g h$ ，其中 $g$ 是地球引力常数。另外，弹簧常数为 $k$ 的理想线性弹簧拉伸至长度 $q$ 时，其势能为 $k q^{2} / 2$ 。在当前模型中，弹簧不是理想的，但它具有非零的静止长度 $l$ 。

本例的数学基础来自 Lobo、Vandenberghe、Boyd 和 Lebret [1]。有关此示例的基于求解器的版本，请参阅使用基于求解器的锥规划最小化分段线性质量-弹簧系统的能量。

数学表示

质量 $i$ 的位置为 $x (i)$ ，水平坐标为 $x_{1} (i)$ ，垂直坐标为 $x_{2} (i)$ 。质量 $i$ 由于 $g m (i) x_{2} (i)$ 的重力而具有势能。弹簧 $i$ 中的势能为 $k (i) (d (i) - l (i))^{2} / 2$ ，其中 $d (i)$ 是质量 $i$ 和质量 $i - 1$ 之间的弹簧长度。以锚点 1 作为质量 0 的位置，以锚点 2 作为质量 $n + 1$ 的位置。前面的能量计算表明，弹簧 $i$ 的势能为

$E n e r g y (i) = \frac{k (i) (‖ x (i) - x (i - 1) ‖ - l (i))^{2}}{2}$ .

将此势能问题重新表述为二阶锥规划问题需要引入一些新变量，如 Lobo [1] 中所述。创建等于项 $E n e r g y (i)$ 的平方根的变量 $t (i)$ 。

$t (i) = \sqrt{\frac{k (i) (‖ x (i) - x (i - 1) ‖ - l (i))^{2}}{2}} .$

令 $e$ 为单位列向量 $[\binom{0}{1}]$ 。则 $x_{2} (i) = e^{T} x (i)$ 。问题变成了

$\min_{x, t} (\sum_{i} g m (i) e^{T} x (i) + ‖ t ‖^{2}) .$ (1)

现在将 $t$ 视为一个自由向量变量，不是由前面的 $t (i)$ 方程给出的。将 $x (i)$ 和 $t (i)$ 之间的关系纳入新的锥约束

$‖ x (i) - x (i - 1) ‖ - l (i) \leq \sqrt{\frac{2}{k (i)}} t (i) .$ (2)

目标函数在其变量中还不是线性的，正如 coneprog 所要求的那样。引入一个新的标量变量 $y$ 。请注意，不等式 $‖ t ‖^{2} \leq y$ 等价于不等式

$‖ [\binom{2 t}{1 - y}] ‖ \leq 1 + y$ .(3)

现在的问题是最小化

$\min_{x, t, y} (\sum_{i} g m (i) e^{T} x (i) + y)$ (4)

受制于 (2) 中列出的 $x (i)$ 和 $t (i)$ 的锥约束以及 (3) 的附加锥约束。锥约束 (3) 确保 $‖ t ‖^{2} \leq y$ 。因此，问题（4）等价于问题（1）。

问题 (4) 中的目标函数和锥约束适合用 coneprog 解。

MATLAB® 表示

定义六个弹簧常数 $k$ 、六个长度常数 $l$ 和五个质量 $m$ 。

k = 40*(1:6);
l = [1 1/2 1 2 1 1/2];
m = [2 1 3 2 1];
g = 9.807;

定义与数学问题变量相对应的优化变量。为了简单起见，将锚点设置为两个虚拟质量点 x(1,:) 和 x(end,:)。这种表示允许每个弹簧在两个质量之间拉伸。

nmass = length(m) + 2;
% k and l have nmass-1 elements
% m has nmass - 2 elements
x = optimvar('x',[nmass,2]);
t = optimvar('t',nmass-1,'LowerBound',0);
y = optimvar('y','LowerBound',0);

创建一个优化问题，并将目标函数设置为（4）中的表达式。

prob = optimproblem;
obj = dot(x(2:(end-1),2),m)*g + y;
prob.Objective = obj;

创建与表达式（2）对应的锥约束。

conecons = optimineq(nmass - 1);
for ii = 1:(nmass-1)
    conecons(ii) = norm(x(ii+1,:) - x(ii,:)) - l(ii) <= sqrt(2/k(ii))*t(ii);
end
prob.Constraints.conecons = conecons;

指定锚点 anchor0 和 anchorn。创建等式约束，指定两个虚拟末端质量位于锚点处。

anchor0 = [0 5];
anchorn = [5 4];
anchorcons = optimeq(2,2);
anchorcons(1,:) = x(1,:) == anchor0;
anchorcons(2,:) = x(end,:) == anchorn;
prob.Constraints.anchorcons = anchorcons;

创建与表达式（3）对应的锥约束。

ycone = norm([2*t;(1-y)]) <= 1 + y;
prob.Constraints.ycone = ycone;

求解问题

问题表示已完成。通过调用 solve 求解问题。

[sol,fval,eflag,output] = solve(prob);

Solving problem using coneprog.
Optimal solution found.

绘制解点和锚点。

plot(sol.x(2:(nmass-1),1),sol.x(2:(nmass-1),2),'ro')
hold on
plot([sol.x(1,1),sol.x(end,1)],[sol.x(1,2),sol.x(end,2)],'ks')
plot(sol.x(:,1),sol.x(:,2),'b--')
legend('Calculated points','Anchor points','Springs','Location',"best")
xlim([sol.x(1,1)-0.5,sol.x(end,1)+0.5])
ylim([min(sol.x(:,2))-0.5,max(sol.x(:,2))+0.5])
hold off

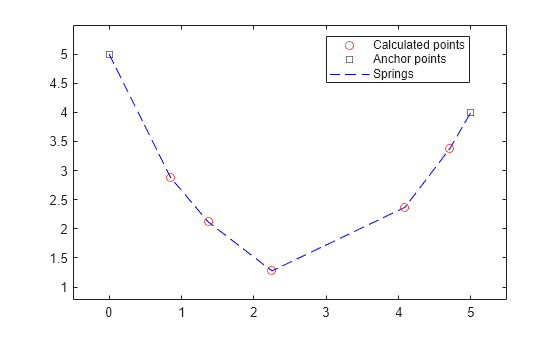
您可以更改参数 m、l 和 k 的值，看看它们如何影响解。您还可以改变质量数；代码会从您提供的数据中获取质量数。

参考资料

[1] Lobo, Miguel Sousa, Lieven Vandenberghe, Stephen Boyd, and Hervé Lebret.“Applications of Second-Order Cone Programming.”Linear Algebra and Its Applications 284, no. 1–3 (November 1998):193–228. https://doi.org/10.1016/S0024-3795(98)10032-0.

另请参阅

coneprog