生成并绘制帕累托前沿

此示例说明如何使用 fgoalattain 为二维多目标函数生成和绘制帕累托前沿。

此示例中的两个目标函数是凸函数 $\sqrt{1 + x^{2}}$ 经平移和缩放的版本。目标函数的代码出现在此示例末尾的 simple_mult 辅助函数中。

这两个目标函数都在区域 $x \leq 0$ 中递减，在区域 $x \geq 1$ 中递增。在 0 和 1 之间， $f_{1} (x)$ 递增， $f_{2} (x)$ 递减，因此存在权衡区域。绘制 $x$ 的两个目标函数，范围从 $- 1 / 2$ 到 $3 / 2$ 。

t = linspace(-1/2,3/2);
F = simple_mult(t);
plot(t,F,'LineWidth',2)
hold on
plot([0,0],[0,8],'g--');
plot([1,1],[0,8],'g--');
plot([0,1],[1,6],'k.','MarkerSize',15);
text(-0.25,1.5,'Minimum(f_1(x))')
text(.75,5.5,'Minimum(f_2(x))')
hold off
legend('f_1(x)','f_2(x)')
xlabel({'x';'Tradeoff region between the green lines'})

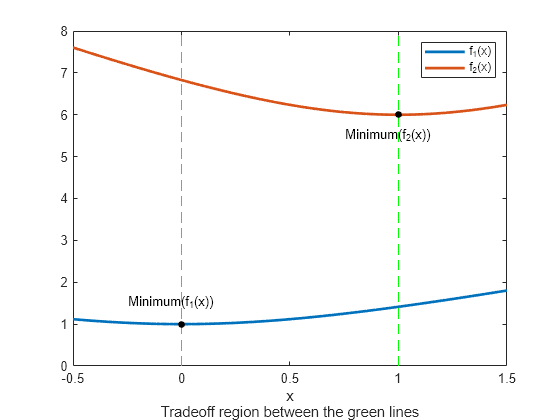
要找到帕累托前沿，首先要找到两个目标函数的无约束最小值。在本例中，您可以从图中看到 $f_{1} (x)$ 的最小值为 1， $f_{2} (x)$ 的最小值为 6，但通常您可能需要使用优化例程来找到最小值。

通常，您可以编写一个返回多目标函数特定分量的函数。（此示例末尾的 pickindex 辅助函数返回第 $k$ 个目标函数值。）然后使用优化求解器找到每个分量的最小值。在本例中您可以使用 fminbnd；对于更高维问题则可使用 fminunc。

k = 1;
[min1,minfn1] = fminbnd(@(x)pickindex(x,k),-1,2);
k = 2;
[min2,minfn2] = fminbnd(@(x)pickindex(x,k),-1,2);

将目标设为每个目标函数不受约束的最优解。要同时实现这些目标，各个目标函数必须互不干扰，但这意味着不存在权衡。

goal = [minfn1,minfn2];

要计算帕累托前沿，对 0 到 1 范围内的 $[a, 1 - a]$ 取权重向量 $a$ 。求解目标达到问题，将权重设置为不同值。

nf = 2; % Number of objective functions
N = 50; % Number of points for plotting
onen = 1/N;
x = zeros(N+1,1);
f = zeros(N+1,nf);
fun = @simple_mult;
x0 = 0.5;
options = optimoptions('fgoalattain','Display','off');
for r = 0:N
t = onen*r; % 0 through 1
weight = [t,1-t];
[x(r+1,:),f(r+1,:)] = fgoalattain(fun,x0,goal,weight,...
[],[],[],[],[],[],[],options);
end
figure
plot(f(:,1),f(:,2),'ko');
xlabel('f_1')
ylabel('f_2')

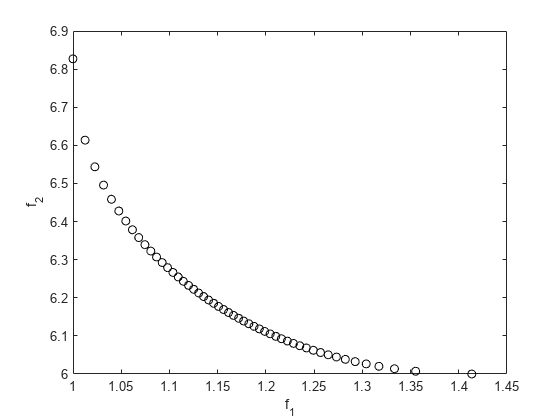
您可以看到两个目标函数之间的权衡。

辅助函数

以下代码创建 simple_multi 函数。

function f = simple_mult(x)
f(:,1) = sqrt(1+x.^2);
f(:,2) = 4 + 2*sqrt(1+(x-1).^2);
end

以下代码创建 pickindex 函数。

function z = pickindex(x,k)
z = simple_mult(x); % evaluate both objectives
z = z(k); % return objective k
end

另请参阅

fgoalattain

生成并绘制帕累托前沿

辅助函数

另请参阅

相关主题

WeChat