使用 fmincon 求解器优化实时编辑器任务
此示例说明如何将基于求解器的优化实时编辑器任务与 fmincon 求解器结合使用,以在受限于线性和非线性约束和边界的情况下最小化二次问题。
设想一个问题,它需要找到能够求解以下问题的 [x1, x2]:
需满足以下约束
此问题的起点 x0 是 x1 = 3 和 x2 = 1。
启动优化实时编辑器任务
点击主页选项卡上文件部分中的新建实时脚本按钮,创建一个新实时脚本。

插入一个优化实时编辑器任务。点击插入选项卡,然后在代码部分中选择任务 > 优化。
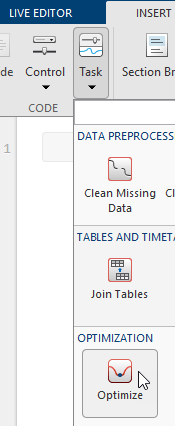

对于此示例,请选择基于求解器的任务。

为了以后用于输入问题数据,请选择插入 > 分节符。新节出现在任务的上方和下方。
输入问题数据
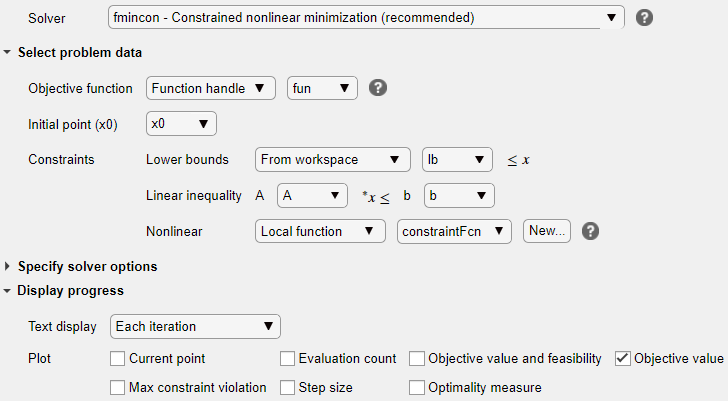
从任务顶部开始,输入问题类型和约束类型。点击目标 > 二次按钮以及约束 > 下界、线性不等式和非线性按钮。任务显示推荐的求解器为
fmincon。目标函数
目标函数足够简单,可以表示为匿名函数。将光标放在任务上方的节中,然后输入以下代码。
fun = @(x)sum(x.^2);
下界
该问题包含下界 x1 ≥ 0.5。将此边界表示为变量
lb。使光标位于定义目标函数的行的末尾,按 Enter 键,并输入以下代码以指定下界。lb = [0.5 -Inf];
初始点
使光标位于定义下界的行的末尾,按 Enter 键,并输入以下代码来设置初始点。
x0 = [3,1];
线性约束
使光标位于定义初始点的行的末尾,按 Enter 键,并输入以下代码来设置线性约束。
A = [-1,-1]; b = -1;
运行节
顶部节现在包含五个参数。
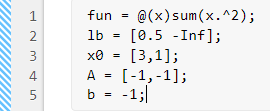
接下来,您需要运行该节,以将参数作为变量放置在工作区中。为此,请点击该节的最左侧区域,该区域包含一个斜线条带。点击此区域后,此条带会变为实心条带,表示变量现在位于工作区中。(注意:您也可以按 Ctrl+Enter 运行该节。)
设置问题数据
在任务的选择问题数据节中输入变量。要指定目标函数,请选择目标函数 > 函数句柄,然后选择 fun。
设置初始点 x0。
选择下界 > 从工作区,然后选择 lb。
在线性不等式区域中设置线性不等式约束变量
A和b。现在指定非线性不等式约束。在选择问题数据节中,选择非线性 > 局部函数,然后点击新建按钮。该函数出现在任务下方的新节中。编辑结果代码以确定包含以下非注释行。
function [c,ceq] = constraintFcn(x) % You can include commented code lines or not. % Be sure that just these uncommented lines remain: c = [-x(1)^2 - x(2)^2 + 1; -9*x(1)^2 - x(2)^2 + 9; -x(1)^2 + x(2); -x(2)^2 + x(1)]; ceq = []; end
在选择问题数据节中,选择 constraintFcn 函数。
监控进度
在任务的显示进度节中,选择文本显示 > 每次迭代,以便您可以监控求解器进度。为绘图选择目标值。
您的设置如下所示:
运行求解器并检查结果
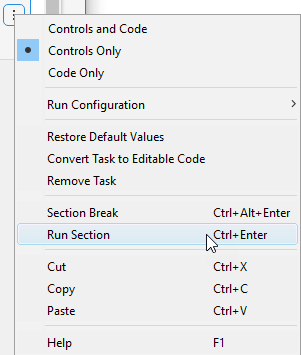
要运行求解器,请点击任务窗口右上角的选项按钮 ⁝,并选择运行节。
绘图出现在单独的图窗窗口中和任务输出区域中。
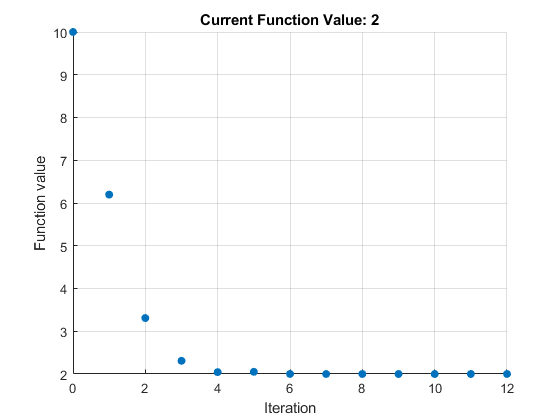
要查看解变量的返回位置,请查看任务的顶部。
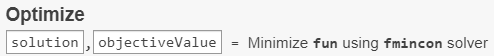
最终点及其相关联的目标函数值出现在工作区中的 solution 和 objectiveValue 变量中。通过在任务下方的实时编辑器节中输入以下代码来查看这些值。
solution, objectiveValue
按 Ctrl+Enter 运行该节。
![solution = [1 1], objectiveValue = 2](optimizelet_fmincon_answer.png)