基于问题的优化的输出函数

此示例说明如何使用输出函数绘制和存储非线性问题的迭代历史记录。该历史记录包括评估点、求解器用于生成点的搜索方向以及评估点处的目标函数值。

有关此示例的基于求解器的方法，请参阅 Optimization Toolbox 的输出函数。

绘图函数与输出函数具有相同的语法，因此此示例也适用于绘图函数。

对于基于求解器的方法和基于问题的方法，根据基于求解器的方法编写输出函数。在基于求解器的方法中，您使用单个向量变量（通常表示为 x），而不是各种大小的优化变量集合。因此，要为基于问题的方法编写输出函数，您必须了解优化变量和基于单个求解器的 x 之间的对应关系。要在优化变量和 x 之间进行映射，请使用 varindex。在此示例中，为了避免与名为 x 的优化变量混淆，使用 "in" 作为向量变量名。

问题描述

问题是最小化变量 x 和 y 的以下函数：

$f = \exp (x) (4 x^{2} + 2 y^{2} + 4 x y + 2 y + 1) .$

此外，该问题还有两个非线性约束：

$\begin{array}{l} x + y - x y \geq 1.5 \\ x y \geq - 10 . \end{array}$

基于问题的设置

为了在基于问题的方法中设置问题，需要定义优化变量和优化问题对象。

x = optimvar('x');
y = optimvar('y');
prob = optimproblem;

将目标函数定义为优化变量中的表达式。

f = exp(x)*(4*x^2 + 2*y^2 + 4*x*y + 2*y + 1);

在 prob 中包含目标函数。

prob.Objective = f;

为了包含非线性约束，创建优化约束表达式。

cons1 = x + y - x*y >= 1.5;
cons2 = x*y >= -10;
prob.Constraints.cons1 = cons1;
prob.Constraints.cons2 = cons2;

因为这是一个非线性问题，所以必须包含一个初始点结构体 x0。使用 x0.x = –1 和 x0.y = 1。

x0.x = -1;
x0.y = 1;

输出函数

outfun 输出函数记录了 fmincon 在迭代过程中生成的点的历史记录。输出函数还绘制点并保留 sqp 算法的搜索方向的单独历史记录。搜索方向是一个从前一个点到 fmincon 尝试的下一个点的向量。在最后一步，输出函数将历史记录保存在工作区变量中，并保存每个迭代步骤中的目标函数值的历史记录。

有关优化输出函数所需的语法，请参阅输出函数和绘图函数语法。

输出函数将单个向量变量作为输入。但当前的问题有两个变数。要找到优化变量和输入变量之间的映射，请使用 varindex。

idx = varindex(prob);
idx.x

ans = 
1

idx.y

ans = 
2

映射显示 x 是变量 1，y 是变量 2。因此，如果输入变量名为 in，那么就是 x = in(1) 和 y = in(2)。

type outfun

function stop = outfun(in,optimValues,state,idx)
     persistent history searchdir fhistory
     stop = false;
 
     switch state
         case 'init'
             hold on
             history = [];
             fhistory = [];
             searchdir = [];
         case 'iter'
         % Concatenate current point and objective function
         % value with history. in must be a row vector.
           fhistory = [fhistory; optimValues.fval];
           history = [history; in(:)']; % Ensure in is a row vector
         % Concatenate current search direction with 
         % searchdir.
           searchdir = [searchdir;... 
                        optimValues.searchdirection(:)'];
           plot(in(idx.x),in(idx.y),'o');
         % Label points with iteration number and add title.
         % Add .15 to idx.x to separate label from plotted 'o'
           text(in(idx.x)+.15,in(idx.y),... 
                num2str(optimValues.iteration));
           title('Sequence of Points Computed by fmincon');
         case 'done'
             hold off
             assignin('base','optimhistory',history);
             assignin('base','searchdirhistory',searchdir);
             assignin('base','functionhistory',fhistory);
         otherwise
     end
 end

通过设置 OutputFcn 选项将输出函数纳入优化中。另外，设置 Algorithm 选项以使用 'sqp' 算法而不是默认的 'interior-point' 算法。将 idx 作为最后一个输入中的额外参数传递给输出函数。请参阅传递额外参数。

outputfn = @(in,optimValues,state)outfun(in,optimValues,state,idx);
opts = optimoptions('fmincon','Algorithm','sqp','OutputFcn',outputfn);

使用输出函数运行优化

使用 'Options' 名称值对参量运行优化，包括输出函数。

[sol,fval,eflag,output] = solve(prob,x0,'Options',opts)

Solving problem using fmincon.

Figure contains an axes object. The axes object with title Sequence of Points Computed by fmincon contains 22 objects of type line, text. One or more of the lines displays its values using only markers

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

sol = struct with fields:
    x: -9.5474
    y: 1.0474

fval = 
0.0236

eflag = 
    OptimalSolution

output = struct with fields:
              iterations: 10
               funcCount: 22
               algorithm: 'sqp'
                 message: 'Local minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the value of the optimality tolerance,↵and constraints are satisfied to within the value of the constraint tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The relative first-order optimality measure, 7.127069e-10,↵is less than options.OptimalityTolerance = 1.000000e-06, and the relative maximum constraint↵violation, 1.065814e-14, is less than options.ConstraintTolerance = 1.000000e-06.'
         constrviolation: 1.0658e-14
                stepsize: 1.4893e-07
            lssteplength: 1
           firstorderopt: 7.1271e-10
            bestfeasible: [1×1 struct]
     objectivederivative: "reverse-AD"
    constraintderivative: "closed-form"
                  solver: 'fmincon'

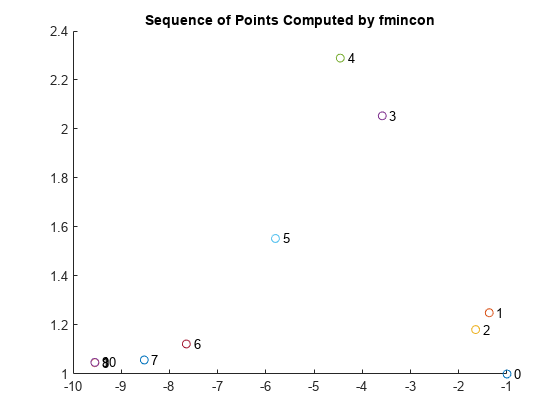
检查迭代历史。optimhistory 矩阵的每一行代表一个点。最后几个点非常接近，这解释了为什么绘制的序列显示第 8、9 和 10 点的数字重叠。

disp('Locations');disp(optimhistory)

Locations
   -1.0000    1.0000
   -1.3679    1.2500
   -1.6509    1.1813
   -3.5870    2.0537
   -4.4574    2.2895
   -5.8015    1.5531
   -7.6498    1.1225
   -8.5223    1.0572
   -9.5463    1.0464
   -9.5474    1.0474
   -9.5474    1.0474

检查 searchdirhistory 和 functionhistory 数组。

disp('Search Directions');disp(searchdirhistory)

Search Directions
         0         0
   -0.3679    0.2500
   -0.2831   -0.0687
   -1.9360    0.8725
   -0.8704    0.2358
   -1.3441   -0.7364
   -2.0877   -0.6493
   -0.8725   -0.0653
   -1.0240   -0.0108
   -0.0011    0.0010
    0.0000   -0.0000

disp('Function Values');disp(functionhistory)

Function Values
    1.8394
    1.8513
    1.7757
    0.9839
    0.6343
    0.3250
    0.0978
    0.0517
    0.0236
    0.0236
    0.0236

不受支持的函数要求 `fcn2optimexpr`

如果您的目标函数或非线性约束函数不是由初等函数组成，则必须使用 fcn2optimexpr 将函数转换为优化表达式。请参阅将非线性函数转换为优化表达式。对于此示例，您需要输入以下代码：

fun = @(x,y)exp(x)*(4*x^2 + 2*y^2 + 4*x*y + 2*y + 1);
f = fcn2optimexpr(fun,x,y);

有关支持的函数列表，请参阅优化变量和表达式支持的运算。

另请参阅

varindex