使用 Optimization Toolbox 实现投资组合多元化

此示例使用:

这个示例展示了投资组合中资产多样化的三种技术。资产多样化的目的是平衡投资组合对任何给定资产的敞口，以减少一段时间内的波动性。考虑到最小方差投资组合对协方差矩阵估计的敏感性，一些从业者在投资组合选择中加入了多样化技术，希望最小化除方差测度之外的其他风险测度，如周转率、最大回撤等。

此示例介绍了这些常见的多样化技术：

等权重 (EW) 投资组合
平等风险贡献 (ERC)
最多元化投资组合 (MDP)

此外，该示例演示了可用于实现不同程度多样化的惩罚方法。在这些方法中，在目标函数中添加了一个惩罚项，以平衡方差减少的水平和投资组合的多样化。

检索市场数据并定义均值-方差投资组合

首先加载并计算预期回报及其协方差矩阵。

% Load data
load('port5.mat');
% Store returns and covariance
mu = mean_return;
Sigma = Correlation .* (stdDev_return * stdDev_return');

使用具有默认约束的 Portfolio (Financial Toolbox) 对象定义均值方差投资组合，以创建完全投资、仅限多头的投资组合。

% Create a mean-variance Portfolio object with default constraints
p = Portfolio('AssetMean',mu,'AssetCovar',Sigma);
p = setDefaultConstraints(p);

Portfolio (Financial Toolbox) 对象的众多特性之一是它可以获得投资组合问题的有效边界。有效边界是通过求解一系列优化问题来计算的，这些问题修改了投资组合的回报水平 $μ_{0}$ 以获得有效边界上的不同点。这些问题定义为

$\begin{array}{l} \min x^{T} Σ x \\ st . \sum_{i = 1}^{n} x_{i} = 1 \\ x^{T} μ \geq μ_{0} \\ x \geq 0 \end{array}$

使用 Portfolio (Financial Toolbox) 对象计算有效边界的优势在于，无需手动构造和求解上面显示的多个优化问题即可获得它。

plotFrontier(p);

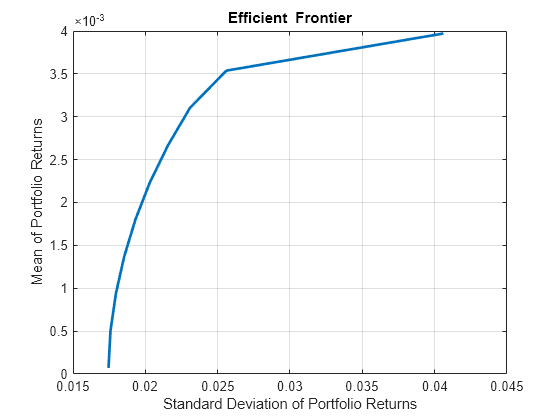
Figure contains an axes object. The axes object with title Efficient Frontier, xlabel Standard Deviation of Portfolio Returns, ylabel Mean of Portfolio Returns contains an object of type line. This object represents Efficient Frontier.

Portfolio (Financial Toolbox) 对象还可以计算与最小方差投资组合相关的权重，这由以下问题定义。

$\begin{array}{l} \min x^{T} Σ x \\ st . \sum_{i = 1}^{n} x_{i} = 1 \\ x \geq 0 \end{array}$

最小方差权重被视为比较所有多样化策略权重的基准。

wMinVar = estimateFrontierLimits(p,'min');

Portfolio (Financial Toolbox)对象可以计算最小方差投资组合。然而，多样化策略对投资组合问题的目标函数进行了修改，而 R2022b 之前的 MATLAB® 版本的 Portfolio (Financial Toolbox) 对象并不支持这些修改。对于早期版本，您必须使用 Optimization Toolbox™ 来求解以下问题。要了解有关 Portfolio (Financial Toolbox) 对象可以求解的问题的更多信息，请参阅 When to Use Portfolio Objects Over Optimization Toolbox (Financial Toolbox)。

指定多样化技术

本节介绍三种多样化方法。三种多样化方法中的每一种都与一种多样化测度相关联，并且该多样化测度用于定义惩罚项以实现不同的多样化水平。通过在目标函数中添加惩罚项获得的多样化范围分别从最小方差投资组合实现的行为到 EW、ECR 和 MDP 的行为。

首先初始化一个optimproblem对象并定义其约束。以下所有投资组合问题都有相同的约束，只有目标函数发生变化。因此，可以重复使用以下 optimproblem，同时重新定义目标函数。

% Define an optimization problem to adjust portfolio diversification
diverseProb = optimproblem('ObjectiveSense','minimize');

默认投资组合只有一个等式约束和资产权重的下界。权重必须非负，并且总和必须为 1。可行集表示为 $X$ ：

$X = {x | x \geq 0, \sum_{i = 1}^{n} x_{i} = 1}$

% Variables
nX = p.NumAssets;
% Portfolio weights [nX-by-1 vector]
x = optimvar('x',nX,1,'LowerBound',0); % x >= 0 (long-only portfolio)

% Equality constraint
% Sum of weights equal to one
diverseProb.Constraints.fullyInvested = sum(x) == 1;

示例的第一部分展示了如何使用 Portfolio (Financial Toolbox) 对象计算最小方差投资组合。但是，也可以使用以下表示最小方差问题的代码来获得最小方差权重：

$\min_{x \in X} x^{T} Σ x$

% Minimize variance
diverseProb.Objective = x'*p.AssetCovar*x;
% Solution of minimum variance portfolio
opts = optimoptions('quadprog','Display','none'); % No output display
[wMinVar2,fMinVar,c,d,e] = solve(diverseProb,'options',opts);

上面的解和Portfolio (Financial Toolbox)对象获得的解并不完全相同。

norm(wMinVar-wMinVar2.x,inf)

ans = 
0.0032

出现这种结果的原因是，考虑到协方差矩阵的特征值的大小，最小方差问题的缩放很差。如果目标函数由一个较大的常数重新调整（例如，1e4），那么两个解在数值精度内就会一致。此功能是使用 Portfolio (Financial Toolbox) 对象的另一个优点。Portfolio (Financial Toolbox) 对象默认重新调整问题以求解数值问题，因此它获得的投资组合的方差比不缩放问题时获得的投资组合的方差更小。

由于该示例的目的是展示不同的多样化策略，因此该示例无需重新调整优化问题的规模。但是，请记住，在下列任何问题中，方差项 ( $x^{T} Σ x$ ) 都可以重新缩放。

等权重 (EW) 投资组合

多样化测度之一是赫芬达尔-赫希曼 (HH) 指数，其定义为：

$HH (x) = \sum_{i = 1}^{n} x_{i}^{2}$

当投资组合权重相等时，该指数最小化。使用该指数作为惩罚获得的投资组合具有满足投资组合约束且权重更均匀的权重。

最小化 HH 指数的投资组合是 $\min_{x \in X} x^{T} x$ 。由于 $X$ 中的约束是默认约束，因此该问题的解是 EW 投资组合。如果 $X$ 有额外的约束，那么解将是满足所有约束的投资组合，同时尽可能保持权重相等。

% Maximize the HH diversification (by minimizing the HH index)
diverseProb.Objective = x'*x;
% Solution that minimizes the HH index
[wHH,fHH] = solve(diverseProb,'options',opts);

使用 HH 惩罚最小化方差的投资组合是 $\min_{x \in X} x^{T} Σ x + λ_{HH} x^{T} x$ 。

% HH penalty parameter
lambdaHH = 1e-2;
% Variance + Herfindahl-Hirschman (HH) index
diverseProb.Objective = x'*p.AssetCovar*x + lambdaHH*(x'*x);
% Solution that accounts for risk and HH diversification
[wHHMix,fHHMix] = solve(diverseProb,'options',opts);

绘制最小方差投资组合、等权重投资组合和惩罚策略的权重分布。

% Plot different strategies
plotAssetAllocationChanges(wMinVar,wHHMix.x,wHH.x)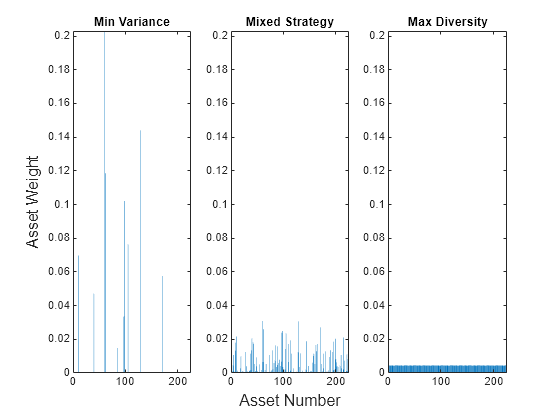

Figure contains 3 axes objects. Axes object 1 with title Min Variance contains an object of type bar. Axes object 2 with title Mixed Strategy contains an object of type bar. Axes object 3 with title Max Diversity contains an object of type bar.

该图显示了惩罚策略如何返回最小方差投资组合和 EW 投资组合之间的权重。事实上，选择 $λ_{HH} = 0$ 可返回最小方差解，而选择 $λ_{HH} \to \infty,$ 可返回接近 EW 投资组合的解。

最多元化投资组合 (MDP)

与最多元化投资组合 (MDP) 相关的多元化指数定义为

$MDP (x) = - \sum_{i = 1}^{n} σ_{i} x_{i}$

其中 $σ_{i}$ 表示资产 $i$ 的标准差。

MDP 是最大化分散化比率的投资组合：

$φ (x) = \frac{x^{T} σ}{\sqrt{x^{T} Σ x}}$

如果投资组合完全投资于一项资产或所有资产完全相关，则多样化比率 $φ (x)$ 等于 1。对于所有其他情况， $φ (x) > 1$ 。如果是 $φ (x) \approx 1$ ，则没有多样化，因此目标是找到最大化 $φ (x)$ 的投资组合：

$\max_{x \in X} \frac{σ^{T} x}{\sqrt{x^{T} Σ x}}$

该问题不再求解上述非线性、非凸优化问题，而是重写为等效凸二次问题。重构遵循了最大化夏普比率的相同想法（Cornuejols & Tütüncü [3]）。等效二次问题的结果如下：

$\begin{array}{l} \min_{y \geq 0, τ \geq 0} y^{T} Σ y \\ s . t σ^{T} y = 1 \\ \sum_{i = 1}^{n} y_{i} = τ \end{array}$

其中 MDP 指标的负数作为该问题的约束出现。这里，MDP 权重由 $\frac{y}{τ}$ 给出。

与 HH 指数不同，MDP 的目标不是获得一个权重在所有资产之间均匀分布的投资组合，而是获得一个选定的（非零）资产与整个投资组合具有相同相关性的投资组合。

% MDP problem
MDPprob = optimproblem('ObjectiveSense','minimize');

% Variables
% Surrogate portfolio weights
y = optimvar('y',nX,1,'LowerBound',0); % y >= 0 (long-only portfolio)
% Auxiliary variable
tau = optimvar('tau',1,1,'LowerBound',0); % tau >= 0

% Constraints
% Sum of stds equal to one
sigma = sqrt(diag(p.AssetCovar));
MDPprob.Constraints.sigmaSumToOne = sigma'*y == 1;
% Sum of weights equal to tau
MDPprob.Constraints.sumToTau = sum(y) == tau;

% Objective
%   min y'*Sigma*y
MDPprob.Objective = y'*p.AssetCovar*y;

% Solve for the MDP
[wMDP,fMDP] = solve(MDPprob,'options',opts);
xMDP = wMDP.y/wMDP.tau;

下面的代码表明存在一个值 ${\hat{λ}}_{MDP} > 0$ ，使得 MDP 问题和带有其惩罚版本的问题是等价的。使用 MDP 惩罚最小化方差的投资组合是 $\min_{x \in X} x^{T} Σ x - λ_{MDP} σ^{T} x$ 。

定义一个 MDP 惩罚参数并求解 MDP。

% MDP penalty parameter
lambdaMDP = 1e-2;
% Variance + Most Diversified Portfolio (MDP)
diverseProb.Objective = x'*p.AssetCovar*x - lambdaMDP*(sigma'*x);
% Solution that accounts for risk and MDP diversification
[wMDPMix,fMDPMix] = solve(diverseProb,'options',opts);

绘制最小方差投资组合、MDP 和惩罚策略的权重分布。

% Plot different strategies
plotAssetAllocationChanges(wMinVar,wMDPMix.x,xMDP)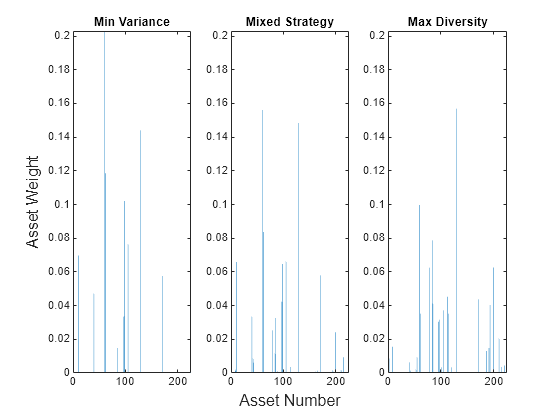

在此图中，惩罚策略权重位于最小方差投资组合和 MDP 之间。该结果与 HH 惩罚相同，其中选择 $λ_{MDP} = 0$ 返回最小方差解，而 $λ_{MDP} \in [0, {\hat{λ}}_{MDP}]$ 的值返回从最小方差行为到 MDP 行为的资产权重。

平等风险贡献 (ERC) 投资组合

与平等风险贡献 (ERC) 投资组合相关的多元化指数定义为

$ERC (x) = - \sum_{i = 1}^{n} \ln (x_{i})$

该指数与 Maillard [1] 所示的凸重构相关，用于计算 ERC 投资组合。作者表明，ERC 投资组合可以通过求解以下优化问题来获得

$\begin{array}{l} \min_{y \geq 0} y^{T} Σ y \\ st . \sum_{i = 1}^{n} \ln (x_{i}) \geq c \end{array}$

并将 $x$ （具有默认约束的 ERC 投资组合）定义为 $x = \frac{y}{\sum_{i} y_{i}}$ ，其中 $c > 0$ 可以是任何常数。

ERC 投资组合的目的是选择资产权重，使得每项资产对投资组合波动的风险贡献对所有资产都是相同的。

% ERC portfolio
ERCprob = optimproblem('ObjectiveSense','minimize');

% Variables
% Surrogate portfolio weights
y = optimvar('y',nX,1,'LowerBound',0); % y >= 0 (long-only portfolio)

% Constraints
% Log constraint
ERCprob.Constraints.logSumIneq = sum(log(y)) >= 1;

% Objective
%   min y'*Sigma*y
ERCprob.Objective = y'*p.AssetCovar*y;

% Solve a nonlinear problem for the ERC portfolio
opts = optimoptions('fmincon','Display','none'); % No output display
w0.y = wMinVar; % Define starting point for fmincon
[wERC,fERC] = solve(ERCprob,w0,'options',opts);
xERC = wERC.y/sum(wERC.y);

使用 ERC 惩罚最小化方差的投资组合是 $\min_{x \in X} x^{T} Σ x - λ_{ERC} \sum_{i = 1}^{n} \ln (x_{i})$ 。

与 MDP 惩罚表示的情况类似，存在 ${\hat{λ}}_{ERC}$ 使得 ERC 问题及其惩罚版本是等价的。

% ERC penalty parameter
lambdaERC = 3e-6; % lambdaERC is so small because the log of a number
                  % close to zero (the portfolio weights) is large.
% Variance + Equal Risk Contribution (ERC)
diverseProb.Objective = x'*p.AssetCovar*x - lambdaERC*sum(log(x));
% Solution that accounts for risk and ERC diversification
[wERCMix,fERCMix] = solve(diverseProb,wHH,'options',opts);

绘制最小方差投资组合、ERC 和惩罚策略的权重分布。

% Plot different strategies
plotAssetAllocationChanges(wMinVar,wERCMix.x,xERC)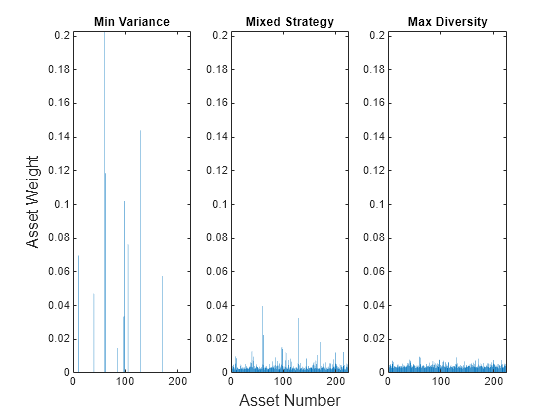

与上面的两种多样化测度类似，这里的惩罚策略权重介于最小方差投资组合和 ERC 投资组合之间。选择 $λ_{ERC} = 0$ 返回最小方差解，而 $λ_{ERC} \in [0, {\hat{λ}}_{ERC}]$ 的值返回从最小方差行为到 ERC 投资组合行为的资产权重。

比较多元化策略

计算每个投资组合中选择的资产数量。假设如果与某项资产相关的权重高于某个阈值，则选择该资产。

% Build a weights table
varNames = {'MinVariance','MixedHH','HH','MixedMDP','MDP', ...
    'MixedERC','ERC'};
weightsTable = table(wMinVar,wHHMix.x,wHH.x,wMDPMix.x,xMDP, ...
    wERCMix.x,xERC,'VariableNames',varNames);
% Number of assets with nonzero weights
cutOff = 1e-3; % Weights below cut-off point are considered zero.
[reweightedTable,TnonZero] = tableWithNonZeroWeights(weightsTable, ...
    cutOff,varNames);
display(TnonZero)

TnonZero=1×7 table
                       MinVariance    MixedHH    HH     MixedMDP    MDP    MixedERC    ERC
                       ___________    _______    ___    ________    ___    ________    ___

    Nonzero weights        11           104      225       23       28       225       225

如上所述，HH 惩罚目标是获得更均匀加权的投资组合。最大化 HH 多样性的投资组合（在仅选择默认约束时对应于 EW 投资组合）具有最多的选定资产，并且这些资产的权重更接近。后一种品质可以在下面的 boxchart 中观察到。此外，将 HH 指数作为罚函数添加到目标的策略所拥有的资产数量比最小方差投资组合多，但比最大化 HH 多样性的投资组合少。ERC 投资组合也选择了所有资产，因为为了具有一定的风险贡献，所有权重都需要非零。

% Boxchart of portfolio's weights
figure;
matBoxPlot = reweightedTable.Variables;
matBoxPlot(matBoxPlot == 0) = NaN;
boxchart(matBoxPlot)
xticklabels(varNames)
title('Weights Distribution')
xlabel('Strategies')
ylabel('Weight')

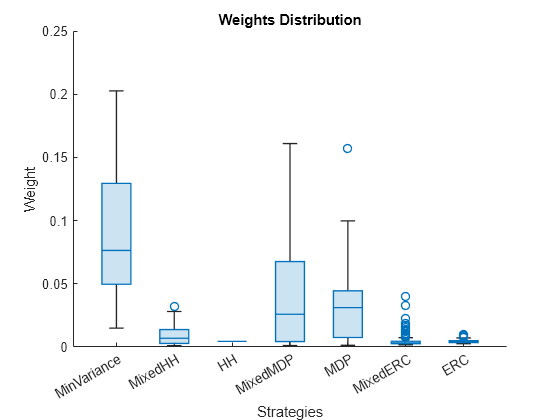
Figure contains an axes object. The axes object with title Weights Distribution, xlabel Strategies, ylabel Weight contains an object of type boxchart.

这个boxchart显示了不同投资组合中资产正权重的分布。如前所述，最大化 HH 多样性的投资组合权重都是相同的。如果投资组合有其他类型的约束，权重不会全部相同，但它们的方差会最低。ERC 投资组合权重也存在较小差异。事实上，您可以观察到，随着资产数量的增加，ERC 投资组合权重的方差变得更小。

MDP 的权重变异性小于最小方差权重的变异性。然而，MDP 权重的变异性并不一定比最小方差权重小，因为 MDP 的目标不是获得等权重资产，而是均匀分布每项资产与其投资组合的相关性。

% Compute and plot the risk contribution of each individual
% asset to the portfolio
riskContribution = portfolioRiskContribution(p.AssetCovar,...
    weightsTable.Variables);
% Remove small contributions
riskContribution(riskContribution < 1e-3) = NaN;

% Compare percent contribution to portfolio risk
boxchart(riskContribution)
xticklabels(varNames)
title('Percent Contributions to Portfolio Risk')
xlabel('Strategies')
ylabel('PCRs')

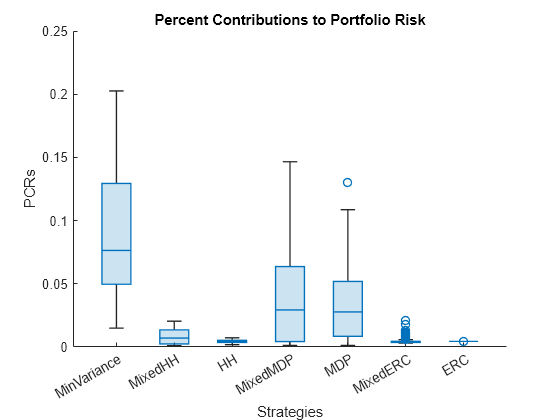
Figure contains an axes object. The axes object with title Percent Contributions to Portfolio Risk, xlabel Strategies, ylabel PCRs contains an object of type boxchart.

这个boxchart显示了每项资产对总投资组合风险的百分比风险贡献。风险贡献百分比计算如下

${(PRC)}_{i} = \frac{x_{i} {(Σ x)}_{i}}{x^{T} Σ x}$

正如预期的那样，所有 ERC 投资组合资产对投资组合的风险贡献都是相同的。正如权重分布图之后所讨论的，如果问题有其他类型的约束，ERC 投资组合的风险贡献对于所有资产来说不会相同，但它们的方差最低。此外，这张图片中显示的行为与权重分布显示的行为类似。

% Compute and plot the correlation of each individual asset to its
% portfolio
corrAsset2Port = correlationInfo(p.AssetCovar,...
    weightsTable.Variables);
% Boxplot of assets to portfolio correlations
figure
boxchart(corrAsset2Port)
xticklabels(varNames)
title('Correlation of Individual Assets to Their Portfolio')
xlabel('Strategies')
ylabel('Correlation')

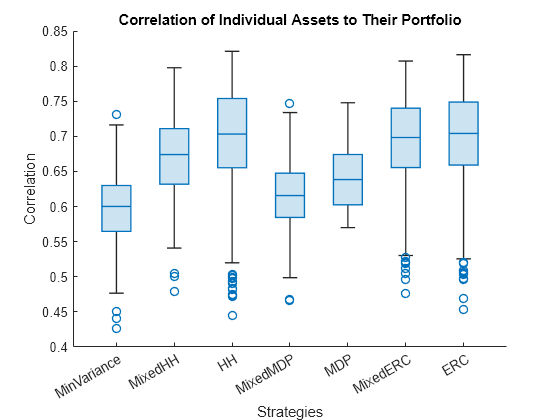
Figure contains an axes object. The axes object with title Correlation of Individual Assets to Their Portfolio, xlabel Strategies, ylabel Correlation contains an object of type boxchart.

这个boxchart显示了每种资产与其各自投资组合的相关性的分布。资产 $i$ 与其投资组合的相关性计算公式如下：

$ρ_{iP} = \frac{{(Σ x)}_{i}}{σ_{i} \sqrt{x^{T} Σ x}}$

MDP 是相关性较紧密的投资组合，其次是使用 MDP 惩罚项的策略。事实上，如果投资组合问题允许负权重，那么 MDP 的所有资产与其投资组合都会具有相同的相关性。此外，HH(EW) 和 ERC 投资组合的相关性变化几乎相同。

参考资料

Maillard, S., Roncalli, T., & Teïletche, J."The Properties of Equally Weighted Risk Contribution Portfolios."The Journal of Portfolio Management, 36(4), 2010, pp. 60-70.
Richard, J. C., & Roncalli, T."Smart Beta:Managing Diversification of Minimum Variance Portfolios."Risk-Based and Factor Investing.Elsevier, 2015, pp. 31-63.
Tütüncü, R., Peña, J., Cornuéjols, G. Optimization Methods in Finance.United Kingdom:Cambridge University Press, 2018.

局部函数

function [] = plotAssetAllocationChanges(wMinVar,wMix,wMaxDiv)
% Plots the weights' allocation from the strategies shown before 

figure
t = tiledlayout(1,3);
nexttile
bar(wMinVar')
axis([0 225 0 0.203])
title('Min Variance')
nexttile
bar(wMix')
axis([0 225 0 0.203])
title('Mixed Strategy')
nexttile
bar(wMaxDiv')
axis([0 225 0 0.203])
title('Max Diversity')
ylabel(t,'Asset Weight')
xlabel(t,'Asset Number')

end

function [weightsTable,TnonZero] = ...
    tableWithNonZeroWeights(weightsTable,cutOff,varNames)
% Creates a table with the number of nonzero weights for each strategy

% Select only meaningful weights
funSelect = @(x) (x >= cutOff).*x./sum(x(x >= cutOff));
weightsTable = varfun(funSelect,weightsTable);

% Number of assets with positive weights
funSum = @(x) sum(x > 0);
TnonZero = varfun(funSum,weightsTable);
TnonZero.Properties.VariableNames = varNames;
TnonZero.Properties.RowNames = {'Nonzero weights'};

end

function [corrAsset2Port] = correlationInfo(Sigma,portWeights)
% Returns a matrix with the correlation of each individual asset to its
% portfolio

nX = size(portWeights,1); % Number of assets
nP = size(portWeights,2); % Number of portfolios

auxM = eye(nX);
corrAsset2Port = zeros(nX,nP);
for j = 1:nP
    % Portfolio's standard deviation
    sigmaPortfolio = sqrt(portWeights(:,j)'*Sigma*portWeights(:,j));
    for i = 1:nX
        % Assets's standard deviation
        sigmaAsset = sqrt(Sigma(i,i));
        % Asset to portfolio correlation
        corrAsset2Port(i,j) = (auxM(:,i)'*Sigma*portWeights(:,j))/...
            (sigmaAsset*sigmaPortfolio);
    end
end

end

function [riskContribution] = portfolioRiskContribution(Sigma,...
    portWeights)
% Returns a matrix with the risk contribution of each asset to
% the underlying portfolio.

nX = size(portWeights,1); % Number of assets
nP = size(portWeights,2); % Number of portfolios

riskContribution = zeros(nX,nP);
for i = 1:nP
    weights = portWeights(:,i);
    % Portfolio variance
    portVar = weights'*Sigma*weights;
    % Marginal constribution to portfoli risk (MCR)
    margRiskCont = weights.*(Sigma*weights)/sqrt(portVar);
    % Percent contribution to portfolio risk
    riskContribution(:,i) = margRiskCont/sqrt(portVar);
end

end

另请参阅

Portfolio (Financial Toolbox)

主题

基于问题的优化工作流
Diversify Portfolios Using Custom Objective (Financial Toolbox)