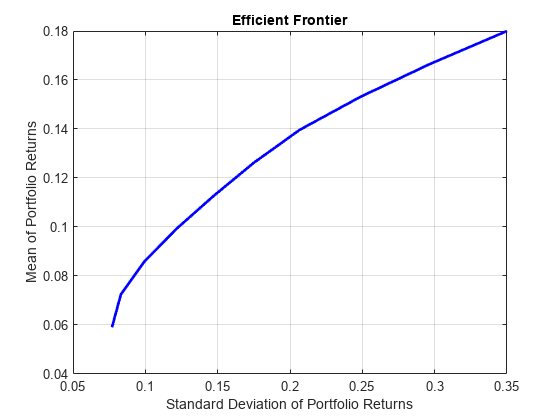
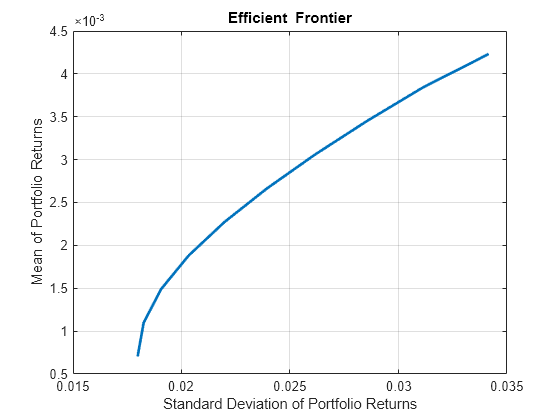
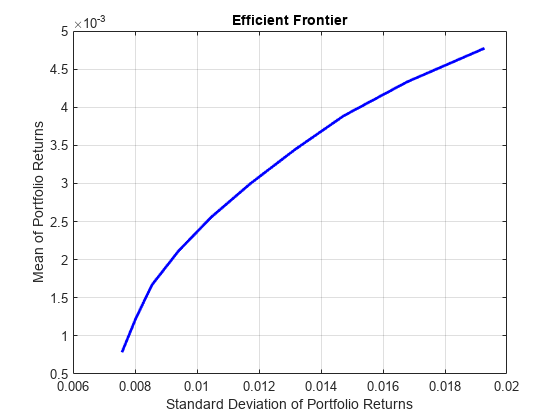
Portfolio

创建 Portfolio 对象以进行均值-方差投资组合优化和分析

说明

使用 Portfolio 函数创建一个 Portfolio 对象，用于均值-方差投资组合优化。

投资组合优化的主要工作流是创建一个 Portfolio 对象实例来完整指定一个投资组合优化问题，并使用支持的函数对 Portfolio 对象进行运算，以求取和分析有效投资组合。有关此工作流的详细信息，请参阅 Portfolio 对象工作流。

您可通过几种方式使用 Portfolio 对象。要使用 Portfolio 对象创建投资组合优化问题，最简单的语法是：

p = Portfolio;

此语法可创建一个 Portfolio 对象 p，其中所有对象属性都为空。

Portfolio 对象也接受用一系列名称-值对组参量指定属性及其值。Portfolio 对象接受采用以下一般语法的输入作为属性：

	p = Portfolio('property1',value1,'property2',value2, ... );

如果已有 Portfolio 对象，则该语法允许且仅允许 Portfolio 对象的第一个参量为已有对象，后续名称-值对组参量则表示要添加或修改的属性。例如，假定已有 Portfolio 对象 p，一般语法为：

p = Portfolio(p,'property1',value1,'property2',value2, ... );

输入参量名称不区分大小写，但必须完整指定。此外，部分属性可采用简写参量名称指定（请参阅简写属性名称）。Portfolio 对象会尝试从输入中检测问题的维度，一旦确定，则对后续输入进行各种标量或矩阵扩展运算，从而简化构建问题的整个过程。此外，Portfolio 对象是值对象，因此，假定有投资组合 p，则以下代码将创建一个不同于 p 的新对象 q：

q = Portfolio(p, ...)

创建 Portfolio 对象后，您可以使用关联的对象函数来设置投资组合约束，分析有效边界并验证投资组合模型。

有关均值-方差优化理论基础的详细信息，请参阅投资组合优化理论。

创建对象

语法

p = Portfolio

p = Portfolio(Name,Value)

p = Portfolio(p,Name,Value)

描述

p = Portfolio 创建一个空的 Portfolio 对象，用于均值-方差投资组合优化和分析。然后，您可以使用支持的 "add" 和 "set" 函数将元素添加到 Portfolio 对象。有关详细信息，请参阅创建 Portfolio 对象。

示例

p = Portfolio(Name,Value) 创建一个 Portfolio 对象（p）并使用名称-值对组设置属性。例如，p = Portfolio('AssetList',Assets(1:12))。您可以指定多个名称-值对组。

示例

p = Portfolio(p,Name,Value) 使用之前创建的 Portfolio 对象 p 创建一个 Portfolio 对象 (p)，并使用名称-值对组设置属性。您可以指定多个名称-值对组。

示例

输入参量

全部展开

`p` — 之前构造的 Portfolio 对象
对象

之前构造的 Portfolio 对象，使用 Portfolio 指定。

属性

全部展开

设置 Portfolio 对象

`AssetList` — 池内资产名称或符号
`[]` (默认) | 字符向量元胞数组 | 字符串数组

池内资产名称或符号，指定为字符向量元胞数组或字符串数组。

数据类型: cell | string

`InitPort` — 初始投资组合
`[]` (默认) | 向量

初始投资组合，指定为向量。

数据类型: double

`Name` — Portfolio 对象实例的名称
`[]` (默认) | 字符向量 | 字符串

Portfolio 对象实例的名称，指定为字符向量或字符串。

数据类型: char | string

`NumAssets` — 池内资产数量
`[]` (默认) | 正整数标量

池内资产数量，指定为正整数标量。

数据类型: double

Portfolio 对象约束

`AEquality` — 线性等式约束矩阵
`[]` (默认) | 矩阵

线性等式约束矩阵，指定为矩阵。有关详细信息，请参阅Linear Equality Constraints。

数据类型: double

`AInequality` — 线性不等式约束矩阵
`[]` (默认) | 矩阵

线性不等式约束矩阵，指定为矩阵。有关详细信息，请参阅Linear Inequality Constraints。

数据类型: double

`bEquality` — 线性等式约束向量
`[]` (默认) | 向量

线性等式约束向量，指定为向量。有关详细信息，请参阅Linear Equality Constraints。

数据类型: double

`bInequality` — 线性不等式约束向量
`[]` (默认) | 向量

线性不等式约束向量，指定为向量。有关详细信息，请参阅Linear Inequality Constraints。

数据类型: double

`GroupA` — 受 B 组权重限制的 A 组权重
`[]` (默认) | 矩阵

受 B 组权重限制的 A 组权重，指定为矩阵。有关详细信息，请参阅Group Constraints。

数据类型: double

`GroupB` — B 组权重
`[]` (默认) | 矩阵

B 组权重，指定为矩阵。有关详细信息，请参阅Group Constraints。

数据类型: double

`GroupMatrix` — 组成员关系矩阵
`[]` (默认) | 矩阵

组成员关系矩阵，指定为矩阵。有关详细信息，请参阅Group Ratio Constraints。

数据类型: double

`LowerBound` — 下界约束
`[]` (默认) | 向量

下界约束，指定为向量。有关详细信息，请参阅'Simple' Bound Constraints和'Conditional' Bound Constraints。

数据类型: double

`LowerBudget` — 下界预算约束
`[]` (默认) | 标量

下界预算约束，指定为标量。有关详细信息，请参阅Budget Constraints。

数据类型: double

`LowerGroup` — 下界组约束
`[]` (默认) | 向量

下界组约束，指定为向量。有关详细信息，请参阅Group Constraints。

数据类型: double

`LowerRatio` — A 组和 B 组之间的最低配置比例
`[]` (默认) | 向量

GroupA 和 GroupB 之间的最低配置比例，指定为向量。有关详细信息，请参阅Group Ratio Constraints。

数据类型: double

`TrackingError` — 跟踪误差约束的上界
`[]` (默认) | 标量

跟踪误差约束的上界，指定为标量。有关详细信息，请参阅Tracking Error Constraints。

数据类型: double

`TrackingPort` — 用于跟踪误差约束的跟踪投资组合
`[]` (默认) | 向量

用于跟踪误差约束的跟踪投资组合，指定为向量。

数据类型: double

`UpperBound` — 上界约束
`[]` (默认) | 向量

上界约束，指定为向量。有关详细信息，请参阅'Simple' Bound Constraints和'Conditional' Bound Constraints。

数据类型: double

`UpperBudget` — 上界预算约束
`[]` (默认) | 标量

上界预算约束，指定为标量。有关详细信息，请参阅Budget Constraints。

数据类型: double

`UpperGroup` — 上界组约束
`[]` (默认) | 向量

上界组约束，指定为向量。有关详细信息，请参阅Group Constraints。

数据类型: double

`UpperRatio` — A 组和 B 组之间的最高配置比例
`[]` (默认) | 向量

GroupA 和 GroupB 之间的最高配置比例，指定为向量。有关详细信息，请参阅Group Ratio Constraints。

数据类型: double

`BoundType` — 每个资产权重的边界类型
`'Simple'` (默认) | 值为 `'Simple'` 或 `'Conditional'` 的字符向量 | 值为 `"Simple"` 或 `"Conditional"` 的字符串 | 值为 `'Simple'` 或 `'Conditional'` 的字符向量元胞数组 | 值为 `"Simple"` 或 `"Conditional"` 的字符串数组

每个资产权重的边界类型，指定为标量字符向量或字符串，或者字符向量元胞数组或字符串数组。有关详细信息，请参阅 setBounds。

数据类型: char | cell | string

`MinNumAssets` — 在投资组合中配置的最小资产数
`[]` (默认) | 数值

在投资组合中配置的最小资产数，指定为标量数值。有关详细信息，请参阅 setMinMaxNumAssets 和Cardinality Constraints。

数据类型: double

`MaxNumAssets` — 在投资组合中配置的最大资产数
`[]` (默认) | 数值

在投资组合中配置的最大资产数，指定为标量数值。有关详细信息，请参阅 setMinMaxNumAssets 和Cardinality Constraints。

数据类型: double

`SellTurnover` — 出售的换手率约束
`[]` (默认) | 标量

出售的换手率约束，指定为标量。有关详细信息，请参阅Average Turnover Constraints和One-Way Turnover Constraints。

数据类型: double

`BuyTurnover` — 购买的换手率约束
`[]` (默认) | 标量

购买的换手率约束，指定为标量。有关详细信息，请参阅Average Turnover Constraints和One-Way Turnover Constraints。

数据类型: double

`Turnover` — 换手率约束
`[]` (默认) | 标量

换手率约束，指定为标量。有关详细信息，请参阅Average Turnover Constraints和One-Way Turnover Constraints。

数据类型: double

Portfolio 对象建模

`AssetCovar` — 资产收益的协方差
`[]` (默认) | 方阵

资产收益的协方差，指定为方阵。

如果 AssetCovar 不是对称半正定矩阵，则使用 nearcorr 为相关矩阵创建半正定矩阵。
在某些情况下，传统的协方差矩阵样本逼近方法表现不佳。一个直观的示例是当变量数目大于观测值数目：这导致了一个不可逆的协方差矩阵。此外，由于协方差估计是使用随机数据的观测值进行的，因此估计器包含一定量的噪声。这种噪声通常会导致病态协方差估计。使用病态矩阵会放大估计误差的影响。您可以使用 covarianceShrinkage 和 covarianceDenoising 来进行协方差估计和降噪。

数据类型: double

`AssetMean` — 资产收益均值
`[]` (默认) | 向量

资产收益的均值，指定为向量。

数据类型: double

`BuyCost` — 比例购买成本
`[]` (默认) | 向量

比例购买成本，指定为向量。有关详细信息，请参阅净投资组合收益。

数据类型: double

`RiskFreeRate` — 无风险率
`[]` (默认) | 标量

无风险率，指定为标量。

数据类型: double

`SellCost` — 比例出售成本
`[]` (默认) | 向量

比例出售成本，指定为向量。有关详细信息，请参阅净投资组合收益。

数据类型: double

对象函数

`setAssetList`	Set up list of identifiers for assets
`setInitPort`	Set up initial or current portfolio
`setDefaultConstraints`	使用总和为 1 的非负权重设置投资组合约束
`getAssetMoments`	从 Portfolio 对象获取资产收益的均值和协方差
`setAssetMoments`	设置 Portfolio 对象资产收益的矩（均值和协方差）
`estimateAssetMoments`	Estimate mean and covariance of asset returns from data
`setCosts`	Set up proportional transaction costs for portfolio
`addEquality`	Add linear equality constraints for portfolio weights to existing constraints
`addGroupRatio`	Add group ratio constraints for portfolio weights to existing group ratio constraints
`addGroups`	Add group constraints for portfolio weights to existing group constraints
`addInequality`	Add linear inequality constraints for portfolio weights to existing constraints
`getBounds`	Obtain bounds for portfolio weights from portfolio object
`getBudget`	Obtain budget constraint bounds from portfolio object
`getCosts`	Obtain buy and sell transaction costs from portfolio object
`getEquality`	Obtain equality constraint arrays from portfolio object
`getGroupRatio`	Obtain group ratio constraint arrays from portfolio object
`getGroups`	Obtain group constraint arrays from portfolio object
`getInequality`	Obtain inequality constraint arrays from portfolio object
`getOneWayTurnover`	Obtain one-way turnover constraints from portfolio object
`setGroups`	Set up group constraints for portfolio weights
`setInequality`	Set up linear inequality constraints for portfolio weights
`setBounds`	Set up bounds for portfolio weights for portfolio
`setBudget`	Set up budget constraints for portfolio
`setCosts`	Set up proportional transaction costs for portfolio
`setEquality`	Set up linear equality constraints for portfolio weights
`setGroupRatio`	Set up group ratio constraints for portfolio weights
`setInitPort`	Set up initial or current portfolio
`setOneWayTurnover`	Set up one-way portfolio turnover constraints
`setTurnover`	Set up maximum portfolio turnover constraint
`setTrackingPort`	Set up benchmark portfolio for tracking error constraint
`setTrackingError`	Set up maximum portfolio tracking error constraint
`setMinMaxNumAssets`	Set cardinality constraints on the number of assets invested in a portfolio
`checkFeasibility`	Check feasibility of input portfolios against portfolio object
`estimateBounds`	Estimate global lower and upper bounds for set of portfolios
`estimateFrontier`	估计有效边界上指定数量的最优投资组合
`estimateFrontierByReturn`	Estimate optimal portfolios with targeted portfolio returns
`estimateFrontierByRisk`	Estimate optimal portfolios with targeted portfolio risks
`estimateFrontierLimits`	Estimate optimal portfolios at endpoints of efficient frontier
`plotFrontier`	绘制有效边界
`estimateMaxSharpeRatio`	估计有效投资组合以最大化 Portfolio 对象的夏普比率
`estimatePortMoments`	估计 Portfolio 对象的投资组合收益矩
`estimatePortReturn`	估计投资组合收益均值
`estimatePortRisk`	Estimate portfolio risk according to risk proxy associated with corresponding object
`estimateCustomObjectivePortfolio`	Estimate optimal portfolio for user-defined objective function for `Portfolio` object
`setSolver`	Choose main solver and specify associated solver options for portfolio optimization
`setSolverMINLP`	Choose mixed integer nonlinear programming (MINLP) solver for portfolio optimization

示例

全部折叠

创建一个空的 Portfolio 对象

打开实时脚本

您可以创建一个不带输入参量的 Portfolio 对象 p，并使用 disp 显示该对象。

p = Portfolio;
disp(p);

  Portfolio with properties:

          BuyCost: []
         SellCost: []
     RiskFreeRate: []
        AssetMean: []
       AssetCovar: []
    TrackingError: []
     TrackingPort: []
         Turnover: []
      BuyTurnover: []
     SellTurnover: []
             Name: []
        NumAssets: []
        AssetList: []
         InitPort: []
      AInequality: []
      bInequality: []
        AEquality: []
        bEquality: []
       LowerBound: []
       UpperBound: []
      LowerBudget: []
      UpperBudget: []
      GroupMatrix: []
       LowerGroup: []
       UpperGroup: []
           GroupA: []
           GroupB: []
       LowerRatio: []
       UpperRatio: []
     MinNumAssets: []
     MaxNumAssets: []
        BoundType: []

借助此方法，您可以使用 Portfolio 函数创建投资组合优化问题。然后，您可以使用相关的 set 函数来设置和修改 Portfolio 对象中的一系列属性。

单步设置创建 Portfolio 对象

打开实时脚本

您可以用变量 m 和 C 指定资产收益的均值和协方差，直接使用 Portfolio 对象来创建“标准”投资组合优化问题。

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];

p = Portfolio('assetmean', m, 'assetcovar', C, ...
'lowerbudget', 1, 'upperbudget', 1, 'lowerbound', 0)

p = 
  Portfolio with properties:

          BuyCost: []
         SellCost: []
     RiskFreeRate: []
        AssetMean: [4x1 double]
       AssetCovar: [4x4 double]
    TrackingError: []
     TrackingPort: []
         Turnover: []
      BuyTurnover: []
     SellTurnover: []
             Name: []
        NumAssets: 4
        AssetList: []
         InitPort: []
      AInequality: []
      bInequality: []
        AEquality: []
        bEquality: []
       LowerBound: [4x1 double]
       UpperBound: []
      LowerBudget: 1
      UpperBudget: 1
      GroupMatrix: []
       LowerGroup: []
       UpperGroup: []
           GroupA: []
           GroupB: []
       LowerRatio: []
       UpperRatio: []
     MinNumAssets: []
     MaxNumAssets: []
        BoundType: []

请注意，LowerBound 属性值进行标量扩展，因为 AssetMean 和 AssetCovar 提供问题的维度。

多步设置创建 Portfolio 对象

打开实时脚本

您也可以用变量 m 和 C 指定资产收益的均值和协方差（这也表明参量名称不区分大小写），采用多步设置来创建同样的“标准”投资组合优化问题。

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];

p = Portfolio;
p = Portfolio(p, 'assetmean', m, 'assetcovar', C);
p = Portfolio(p, 'lowerbudget', 1, 'upperbudget', 1);
p = Portfolio(p, 'lowerbound', 0);
 
plotFrontier(p);

这种方法之所以有效，是因为对 Portfolio 的调用是按此特定顺序进行的。在本例中，初始化 AssetMean 和 AssetCovar 的那次调用确定了问题的维度。如果您最后执行这次调用，则必须显式设置 LowerBound 属性的维度，如下所示：

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];

p = Portfolio;
p = Portfolio(p, 'LowerBound', zeros(size(m)));
p = Portfolio(p, 'LowerBudget', 1, 'UpperBudget', 1);
p = Portfolio(p, 'AssetMean', m, 'AssetCovar', C);
 
plotFrontier(p);

如果未指定 LowerBound 的大小，而是输入标量参量，则 Portfolio 对象假设您正在定义单资产问题，并在设置包含四个资产的资产矩的调用中产生错误。

使用简写属性名称创建 Portfolio 对象

打开实时脚本

使用 Portfolio 创建 Portfolio 对象 p 时，您可以使用简写属性名称。

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];

p = Portfolio('mean', m, 'covar', C, 'budget', 1, 'lb', 0)

p = 
  Portfolio with properties:

          BuyCost: []
         SellCost: []
     RiskFreeRate: []
        AssetMean: [4x1 double]
       AssetCovar: [4x4 double]
    TrackingError: []
     TrackingPort: []
         Turnover: []
      BuyTurnover: []
     SellTurnover: []
             Name: []
        NumAssets: 4
        AssetList: []
         InitPort: []
      AInequality: []
      bInequality: []
        AEquality: []
        bEquality: []
       LowerBound: [4x1 double]
       UpperBound: []
      LowerBudget: 1
      UpperBudget: 1
      GroupMatrix: []
       LowerGroup: []
       UpperGroup: []
           GroupA: []
           GroupB: []
       LowerRatio: []
       UpperRatio: []
     MinNumAssets: []
     MaxNumAssets: []
        BoundType: []

直接设置 Portfolio 对象属性

打开实时脚本

虽然不推荐，但您可以直接设置属性，然而系统不会对输入进行错误检查。

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];

p = Portfolio;
p.NumAssets = numel(m);
p.AssetMean = m;
p.AssetCovar = C;
p.LowerBudget = 1;
p.UpperBudget = 1;
p.LowerBound = zeros(size(m));
disp(p)

  Portfolio with properties:

          BuyCost: []
         SellCost: []
     RiskFreeRate: []
        AssetMean: [4x1 double]
       AssetCovar: [4x4 double]
    TrackingError: []
     TrackingPort: []
         Turnover: []
      BuyTurnover: []
     SellTurnover: []
             Name: []
        NumAssets: 4
        AssetList: []
         InitPort: []
      AInequality: []
      bInequality: []
        AEquality: []
        bEquality: []
       LowerBound: [4x1 double]
       UpperBound: []
      LowerBudget: 1
      UpperBudget: 1
      GroupMatrix: []
       LowerGroup: []
       UpperGroup: []
           GroupA: []
           GroupB: []
       LowerRatio: []
       UpperRatio: []
     MinNumAssets: []
     MaxNumAssets: []
        BoundType: []

创建 `Portfolio` 对象并确定有效投资组合

打开实时脚本

创建有效投资组合：

load CAPMuniverse

p = Portfolio('AssetList',Assets(1:12));
p = estimateAssetMoments(p, Data(:,1:12),'missingdata',true);
p = setDefaultConstraints(p);
plotFrontier(p);

pwgt = estimateFrontier(p, 5);

pnames = cell(1,5);
for i = 1:5
	pnames{i} = sprintf('Port%d',i);
end

Blotter = dataset([{pwgt},pnames],'obsnames',p.AssetList);

disp(Blotter);

            Port1        Port2       Port3       Port4      Port5
    AAPL     0.017926    0.058247    0.097816    0.12955    0    
    AMZN            0           0           0          0    0    
    CSCO            0           0           0          0    0    
    DELL    0.0041906           0           0          0    0    
    EBAY            0           0           0          0    0    
    GOOG      0.16144     0.35678     0.55228    0.75116    1    
    HPQ      0.052566    0.032302    0.011186          0    0    
    IBM       0.46422     0.36045     0.25577    0.11928    0    
    INTC            0           0           0          0    0    
    MSFT      0.29966     0.19222    0.082949          0    0    
    ORCL            0           0           0          0    0    
    YHOO            0           0           0          0    0

混合整数均值-方差投资组合优化问题

打开实时脚本

此示例说明如何求解具有选定资产数量或条件（半连续）边界约束的均值方差投资组合优化问题。若要求解此问题，您可以使用 Portfolio 对象以及不同的混合整数非线性规划 (MINLP) 求解器。

均值-方差投资组合

加载 CAPMuniverse.mat 中的收益数据。然后，使用默认约束创建一个权重总和为 1 的纯多头投资组合均值方差 Portfolio 对象。对于此示例，您可以将权重 $X$ 的可行域定义为

$X = {x | \sum_{i = 1}^{n} x_{i} = 1, x_{i} \geq 0} .$

% Load data
load CAPMuniverse.mat

% Create a mean-variance Portfolio object with default constraints
p = Portfolio(AssetList=Assets(1:12));
p = estimateAssetMoments(p,Data(:,1:12));
p = setDefaultConstraints(p);

通过设置条件（半连续）边界来包含此场景的二元变量。条件边界是指 $x_{i} = 0$ 或 $x_{i} \geq ℓ_{i}$ 这样的边界。在此示例中，所有资产的边界为 $ℓ_{i} = 0.1$ 。

% Set conditional bounds
condLB = 0.1;
condUB = 0.5;
p = setBounds(p,condLB,condUB,BoundType="conditional");

使用 estimateFrontier 估计有效边界上的一组投资组合。有效边界是一条曲线，该曲线显示帕累托最优投资组合实现的收益和风险之间的平衡。对于给定的收益水平，有效边界上的投资组合是指在保持期望收益的同时将风险降至最低的投资组合。与之相对，对于给定的风险水平，有效边界上的投资组合是指在保持预期风险水平的同时最大化收益的投资组合。

% Compute efficient frontier
pwgt = estimateFrontier(p)

pwgt = 12×10

         0         0    0.1000    0.1253    0.1745    0.2236    0.2715    0.3327    0.4111    0.5000
         0         0         0         0         0         0         0         0         0         0
         0         0         0         0         0         0         0         0         0         0
    0.1350         0         0         0         0         0         0         0         0         0
         0         0         0         0         0         0         0         0         0         0
    0.1000    0.1450    0.1406    0.1910    0.2344    0.2778    0.3200    0.3726    0.4415    0.5000
    0.1000    0.1609    0.1642    0.2121    0.2415    0.2709    0.3085    0.2947    0.1474         0
    0.2354    0.1875    0.1290         0         0         0         0         0         0         0
         0         0         0         0         0         0         0         0         0         0
    0.4296    0.4066    0.3662    0.3717    0.2496    0.1277         0         0         0         0
      ⋮

% Compute risk and returns of the portfolios on the efficient frontier
[rsk,ret] = estimatePortMoments(p,pwgt)

使用 plotFrontier 根据边界估计值绘制权重。生成的曲线呈分段凹形，凹区间之间有垂直跳跃（不连续性）。

% Plot efficient frontier
plotFrontier(p,pwgt)

更改 MINLP 求解器

在上一部分，您使用了 estimateFrontier 的默认求解器。但其实您可以使用 setSolverMINLP 支持的下面三种算法中的任意一种来求解混合整数投资组合问题：OuterApproximation、ExtendedCP 和 TrustRegionCP。此外，OuterApproximation 算法在求解 Portfolo 问题时还接受一个额外的名称-值参量 (ExtendedFormulation)，可以重新表述问题的二次函数形式，从而能够在扩展空间中进行处理，这通常会减少计算时间。包括 OuterApproximation 算法的扩展公式变体在内的所有算法，都会在数值精度范围内返回相同的值。可用的求解器包括：

OuterApproximation - 默认算法，该算法非常稳健，通常比 ExtenedCP 速度更快
OuterApproximation，其中 ExtendedFormulation 设置为 true - 一种稳健的算法，通常比其他算法更快，但仅支持求解 Portfolio 对象问题
ExtendedCP - 该求解器稳健性最佳，但通常速度最慢
TrustRegionCP - 该算法速度最快，但稳健性较差，可能提供次优解

有关混合整数投资组合问题求解器的详细信息，请参阅Choose MINLP Solvers for Portfolio Problems。

若要更改 MINLP 求解器，请使用 setSolverMINLP。

% Select the extended formulation version of 'OuterApproximation'
p_EOA = setSolverMINLP(p,'OuterApproximation',...
    ExtendedFormulation=true);
pwgt_EOA = estimateFrontier(p_EOA);
[rskEOA,retEOA] = estimatePortMoments(p_EOA,pwgt_EOA);

% Select 'TrustRegionCP' as solver
p_TR = setSolverMINLP(p,'TrustRegionCP');
pwgt_TR = estimateFrontier(p_TR);
[rskTR,retTR] = estimatePortMoments(p_TR,pwgt_TR);

% Select 'ExtendedCP' as solver using 'midway' cuts as 'CutGeneration'
p_ECP = setSolverMINLP(p,'ExtendedCP','CutGeneration','midway');
pwgt_ECP = estimateFrontier(p_ECP);
[rskECP,retECP] = estimatePortMoments(p_ECP,pwgt_ECP);

比较使用不同的求解器得到的有效边界上的投资组合收益和风险。它们在数值精度内是相同的，其中绝对误差为 $\leq 10^{- 4}$ 。

retTable = table(ret,retEOA,retTR,retECP,...
    'VariableNames',{'OA','EOA','TR','ECP'})

retTable=10×4 table
        OA           EOA            TR           ECP    
    __________    __________    __________    __________

    0.00078336    0.00078336    0.00078334    0.00078348
     0.0012267     0.0012267     0.0012267     0.0012268
       0.00167       0.00167       0.00167     0.0016701
     0.0021133     0.0021133     0.0021133     0.0021134
     0.0025566     0.0025566     0.0025566     0.0025567
     0.0029999     0.0029999     0.0029999         0.003
     0.0034432     0.0034432     0.0034432     0.0034433
     0.0038865     0.0038865     0.0038865     0.0038866
     0.0043298     0.0043298     0.0043298     0.0043299
     0.0047731     0.0047731     0.0047731     0.0047731

rskTable = table(rsk,rskEOA,rskTR,rskECP,...
    'VariableNames',{'OA','EOA','TR','ECP'})

rskTable=10×4 table
       OA           EOA          TR           ECP   
    _________    _________    _________    _________

    0.0075778    0.0075778    0.0075778    0.0075778
    0.0080234    0.0080234    0.0080235    0.0080236
    0.0085488    0.0085488    0.0085488     0.008549
    0.0094024    0.0094024     0.009405    0.0094025
     0.010456     0.010456     0.010456     0.010456
     0.011727     0.011727     0.011776     0.011728
     0.013155     0.013155     0.013155     0.013155
     0.014729     0.014729     0.014729     0.014729
     0.016764     0.016764     0.016764     0.016764
     0.019273     0.019273     0.019273     0.019273

% Compare risks from the different OuterApproximation formulations
norm(rskTable.OA-rskTable.EOA,Inf) <= 1e-4

ans = logical
   1

详细信息

全部展开

均值-方差投资组合优化

均值-方差优化问题可以由三个元素完整指定。

均值-方差优化问题的三个元素是：

资产池，包含对某一时期内资产总收益的预期均值和协方差所作的估计。
一个投资组合集，根据一系列约束指定一组投资组合选择。
一个模型，表示投资组合收益和风险，在均值-方差优化中，即投资组合收益的总均值或净均值，以及投资组合收益的标准差。

在明确指定这三个元素后，您可以求解和分析投资组合优化问题。最简单的均值-方差投资组合优化问题包括：

资产总收益的均值和协方差
所有投资组合的非负权重，总和为 1（求和约束称为预算约束）
投资组合收益和风险的内置模型，采用了资产总收益的均值和协方差

有关 Financial Toolbox™ 中投资组合优化工具支持的均值-方差优化理论和定义的详细信息，请参阅投资组合优化理论。

投资组合问题充分性

如果满足两个条件，则均值-方差投资组合优化问题可由 Portfolio 对象完整指定。

以下是必须满足的两个条件：

必须指定资产收益矩，以使属性 AssetMean 包含资产收益的有效有限均值向量，且属性 AssetCovar 包含资产收益协方差的有效对称正半定矩阵。
要满足第一个条件，可以设置与资产收益矩相关的属性。
可行投资组合集必须是非空紧凑集，其中紧凑集是封闭且有界的。
要满足第二个条件，需要由多个属性定义不同类型的约束以形成一组可行投资组合。由于此类集合必须是有界的，因此可以施加显式或隐式约束，您可以使用 estimateBounds 等函数来确保恰当地表示问题。

假定资产收益的均值和协方差分别为变量 AssetMean 和 AssetCovar，此问题可完整指定如下：

p = Portfolio('AssetMean', AssetMean, 'AssetCovar', AssetCovar,...
'LowerBound', 0, 'UpperBudget',1, 'LowerBudget',1)

或等效指定为：

p = Portfolio;
p = setAssetMoments(p, AssetMean, AssetCovar); 
p = setDefaultConstraints(p);

虽然均值-方差投资组合优化的一般充分条件不止这两个条件，但在 Financial Toolbox 中实现的 Portfolio 对象会隐式处理这些额外条件。有关均值-方差投资组合优化的马科维茨模型的详细信息，请参阅 Portfolio Optimization。

简写属性名称

Portfolio 对象支持部分参量名称简写，以替代 Portfolio 对象某些属性的较长参量名称。

例如，除了 'assetcovar'，Portfolio 对象也支持使用名称 'covar'（不区分大小写）设置 Portfolio 对象的 AssetCovar 属性。每个简写参量名称对应于 Portfolio 对象的一个属性。唯一的例外是简写参量名称 'budget'，它既可以表示 LowerBudget 属性，也可以表示 UpperBudget 属性。当使用 'budget' 时，则 LowerBudget 和 UpperBudget 属性设置为相同的值以构成等式预算约束。

简写属性名称

简写参量名称	等效参量 / 属性名称
`ae`	`AEquality`
`ai`	`AInequality`
`covar`	`AssetCovar`
`assetnames` 或 `assets`	`AssetList`
`mean`	`AssetMean`
`be`	`bEquality`
`bi`	`bInequality`
`group`	`GroupMatrix`
`lb`	`LowerBound`
`n` 或 `num`	`NumAssets`
`rfr`	`RiskFreeRate`
`ub`	`UpperBound`
`budget`	`UpperBudget` 和 `LowerBudget`

参考

[1] For a complete list of references for the Portfolio object, see Portfolio Optimization.

版本历史记录

在 R2011a 中推出

另请参阅

主题

外部网站

投资组合优化入门（4 分 12 秒）

Portfolio

说明

创建对象

语法

描述

输入参量

p — 之前构造的 Portfolio 对象 对象

属性

设置 Portfolio 对象

AssetList — 池内资产名称或符号 [] (默认) | 字符向量元胞数组 | 字符串数组

InitPort — 初始投资组合 [] (默认) | 向量

Name — Portfolio 对象实例的名称 [] (默认) | 字符向量 | 字符串

NumAssets — 池内资产数量 [] (默认) | 正整数标量

Portfolio 对象约束

AEquality — 线性等式约束矩阵 [] (默认) | 矩阵

AInequality — 线性不等式约束矩阵 [] (默认) | 矩阵

bEquality — 线性等式约束向量 [] (默认) | 向量

bInequality — 线性不等式约束向量 [] (默认) | 向量

GroupA — 受 B 组权重限制的 A 组权重 [] (默认) | 矩阵

GroupB — B 组权重 [] (默认) | 矩阵

GroupMatrix — 组成员关系矩阵 [] (默认) | 矩阵

LowerBound — 下界约束 [] (默认) | 向量

LowerBudget — 下界预算约束 [] (默认) | 标量

LowerGroup — 下界组约束 [] (默认) | 向量

LowerRatio — A 组和 B 组之间的最低配置比例 [] (默认) | 向量

TrackingError — 跟踪误差约束的上界 [] (默认) | 标量

TrackingPort — 用于跟踪误差约束的跟踪投资组合 [] (默认) | 向量

UpperBound — 上界约束 [] (默认) | 向量

UpperBudget — 上界预算约束 [] (默认) | 标量

UpperGroup — 上界组约束 [] (默认) | 向量

UpperRatio — A 组和 B 组之间的最高配置比例 [] (默认) | 向量

BoundType — 每个资产权重的边界类型 'Simple' (默认) | 值为 'Simple' 或 'Conditional' 的字符向量 | 值为 "Simple" 或 "Conditional" 的字符串 | 值为 'Simple' 或 'Conditional' 的字符向量元胞数组 | 值为 "Simple" 或 "Conditional" 的字符串数组

MinNumAssets — 在投资组合中配置的最小资产数 [] (默认) | 数值

MaxNumAssets — 在投资组合中配置的最大资产数 [] (默认) | 数值

SellTurnover — 出售的换手率约束 [] (默认) | 标量

BuyTurnover — 购买的换手率约束 [] (默认) | 标量

Turnover — 换手率约束 [] (默认) | 标量

Portfolio 对象建模

AssetCovar — 资产收益的协方差 [] (默认) | 方阵

AssetMean — 资产收益均值 [] (默认) | 向量

BuyCost — 比例购买成本 [] (默认) | 向量

RiskFreeRate — 无风险率 [] (默认) | 标量

SellCost — 比例出售成本 [] (默认) | 向量

对象函数

示例

创建一个空的 Portfolio 对象

单步设置创建 Portfolio 对象

多步设置创建 Portfolio 对象

使用简写属性名称创建 Portfolio 对象

直接设置 Portfolio 对象属性

创建 Portfolio 对象并确定有效投资组合

混合整数均值-方差投资组合优化问题

详细信息

均值-方差投资组合优化

投资组合问题充分性

简写属性名称

参考

版本历史记录

另请参阅

主题

外部网站

WeChat

`p` — 之前构造的 Portfolio 对象
对象

`AssetList` — 池内资产名称或符号
`[]` (默认) | 字符向量元胞数组 | 字符串数组

`InitPort` — 初始投资组合
`[]` (默认) | 向量

`Name` — Portfolio 对象实例的名称
`[]` (默认) | 字符向量 | 字符串

`NumAssets` — 池内资产数量
`[]` (默认) | 正整数标量

`AEquality` — 线性等式约束矩阵
`[]` (默认) | 矩阵

`AInequality` — 线性不等式约束矩阵
`[]` (默认) | 矩阵

`bEquality` — 线性等式约束向量
`[]` (默认) | 向量

`bInequality` — 线性不等式约束向量
`[]` (默认) | 向量

`GroupA` — 受 B 组权重限制的 A 组权重
`[]` (默认) | 矩阵

`GroupB` — B 组权重
`[]` (默认) | 矩阵

`GroupMatrix` — 组成员关系矩阵
`[]` (默认) | 矩阵

`LowerBound` — 下界约束
`[]` (默认) | 向量

`LowerBudget` — 下界预算约束
`[]` (默认) | 标量

`LowerGroup` — 下界组约束
`[]` (默认) | 向量

`LowerRatio` — A 组和 B 组之间的最低配置比例
`[]` (默认) | 向量

`TrackingError` — 跟踪误差约束的上界
`[]` (默认) | 标量

`TrackingPort` — 用于跟踪误差约束的跟踪投资组合
`[]` (默认) | 向量

`UpperBound` — 上界约束
`[]` (默认) | 向量

`UpperBudget` — 上界预算约束
`[]` (默认) | 标量

`UpperGroup` — 上界组约束
`[]` (默认) | 向量

`UpperRatio` — A 组和 B 组之间的最高配置比例
`[]` (默认) | 向量

`MinNumAssets` — 在投资组合中配置的最小资产数
`[]` (默认) | 数值

`MaxNumAssets` — 在投资组合中配置的最大资产数
`[]` (默认) | 数值

`SellTurnover` — 出售的换手率约束
`[]` (默认) | 标量

`BuyTurnover` — 购买的换手率约束
`[]` (默认) | 标量

`Turnover` — 换手率约束
`[]` (默认) | 标量

`AssetCovar` — 资产收益的协方差
`[]` (默认) | 方阵

`AssetMean` — 资产收益均值
`[]` (默认) | 向量

`BuyCost` — 比例购买成本
`[]` (默认) | 向量

`RiskFreeRate` — 无风险率
`[]` (默认) | 标量

`SellCost` — 比例出售成本
`[]` (默认) | 向量

创建 `Portfolio` 对象并确定有效投资组合