covarianceDenoising
Syntax
Description
SigmaHat = covarianceDenoising(AssetReturns)
In addition, you can use covarianceShrinkage to compute an estimate of covariance matrix
using shrinkage estimation. For information on which covariance estimation method to
choose, see Comparison of Methods for Covariance Estimation.
SigmaHat = covarianceDenoising(Sigma,SampleSize)Sigma) and the sample size used to estimate the initial
covariance (sampleSize).
[
returns a covariance estimate and the number of eigenvalues that are associated with
signal in combination with either of the input argument combinations in the previous
syntaxes.SigmaHat,numSignalEig] = covarianceDenoising(___)
Examples
Input Arguments
Output Arguments
More About
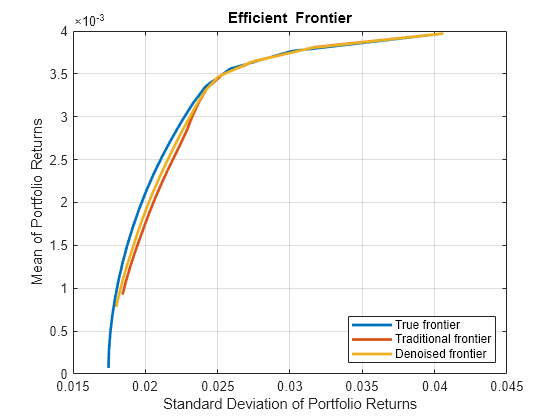
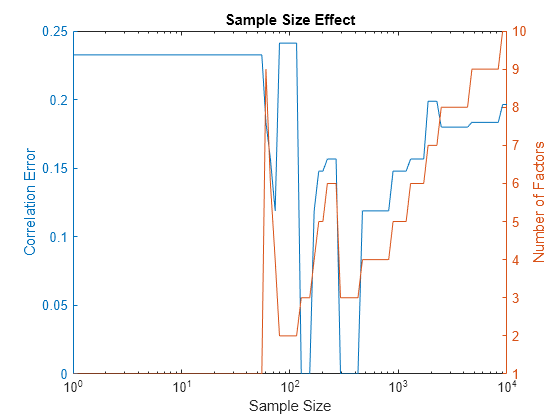
Algorithms
The covarianceDenoising function shrinks only the part of the
covariance that corresponds with noise as follows:
Compute the correlation matrix C associated with the traditional covariance estimate Σ.
Compute the eigendecomposition of C = VΛ VT.
Estimate the empirical distribution of the eigenvalues using kernel density estimation with
fitdist(x,'Kernel'). For more information, seefitdist.Fit the Marchenko-Pastur distribution to the empirical distribution by minimizing the mean squared error (MSE) between the empirical probability density function (pdf) and the fitted Marchenko-Pastur pdf. This gives the theoretical bounds λ+ and λ- on the eigenvalues associated with noise.
Let be the average of the eigenvalues smaller than λ+. Set all eigenvalues smaller than λ+ to . These are the eigenvalues associated with noise.
Compute the denoised version of the correlation matrix and rescale so that the main diagonal only has ones. is a correlation matrix.
Compute the denoised covariance estimate from .
References
[1] Lòpez de Prado, M. Machine Learning for Asset Managers (Elements in Quantitative Finance). Cambridge University Press, 2020.
Version History
Introduced in R2023a