Compare Performance of Covariance Denoising with Factor Modeling Using Backtesting

Open Live Script

This example uses backtesting to compare the performance of two investment strategies that use factor information to compute the portfolio weights. The first investment strategy uses covarianceDenoising to estimate both the covariance matrix and the number of factors to use in the second investment strategy. The second investment strategy uses a principal component analysis (PCA) factor model to estimate the covariance matrix with the number of factors obtained with covarianceDenoising. The PCA factor model follows the process in Portfolio Optimization Using Factor Models.

Load Data

Load a simulated data set that includes asset returns for a total $n = 100$ assets and 2000 daily observations.

load('asset_return_100_simulated.mat');
[numObservations,numAssets] = size(stockReturns)

numObservations = 
2000

numAssets = 
100

Create a timetable of asset prices from the asset returns.

% Convert the returns to prices
pricesT = ret2tick(stockReturns,'StartPrice',100);

% Create timetable
rowTimes = datetime("today"):datetime("today")+numObservations;
pricesTT = table2timetable(pricesT,'RowTimes',rowTimes);

Visualize the equity curve for each stock. For this example, plot the first five stocks.

figure;
plot(0:2000,pricesTT{:,1:5})
xlabel('Timestep');
ylabel('Value');
title('Equity Curve');
legend(pricesTT.Properties.VariableNames(1:5));

Figure contains an axes object. The axes object with title Equity Curve, xlabel Timestep, ylabel Value contains 5 objects of type line. These objects represent Asset1, Asset2, Asset3, Asset4, Asset5.

Optimize Asset Allocation Using Covariance Denoising

Covariance denoising is a technique that you can use to reduce the noise and enhance the signal in a covariance matrix. First, the eigenvalues that are associated with noise are separated from the eigenvalues associated with signal. Then, the eigenvalues associated with noise are shrunk towards a target value. This technique helps improve the stability of the covariance matrix over time as well as its condition number.

The function covarianceDenoising computes the denoised estimate of the covariance matrix and returns as a second output the number of eigenvalues identified with signal. You use this number in the Optimize the Asset Allocation Using Factor Modeling section to determine the number of factors that the factor model allocation uses.

This example uses the first 42 days (approximately 2 months) of the data set to select the initial portfolio allocations.

% Warm-up period
warmupPeriod = 42;

% No current weights (100% cash position)
w0 = zeros(1,numAssets);

% Warm-up partition of prices timetable
warmupTT = pricesTT(1:warmupPeriod,:);

Compute the maximum return portfolio subject to a target risk of 0.008 using the denoised covariance estimate.

% Compute weights with denoised strategy
wDenoised_initial = denoising(w0,warmupTT);

Check for asset allocations that are over 5% to identify assets with large investment weights.

percentage = 0.05;
AssetName = pricesTT.Properties.VariableNames(...
    wDenoised_initial>=percentage)';
Weight = wDenoised_initial(wDenoised_initial>=percentage);
T1 = table(AssetName,Weight)

T1=5×2 table
     AssetName      Weight 
    ___________    ________

    {'Asset6' }    0.066014
    {'Asset47'}     0.10991
    {'Asset50'}     0.24654
    {'Asset75'}     0.11752
    {'Asset94'}     0.31708

Optimize Asset Allocation Using Factor Modeling

For factor modeling, you can use statistical factors extracted from the asset return series. In this example, PCA is used to extract these factors [1]. You can then use this factor model to solve the portfolio optimization problem.

With a factor model, $n$ asset returns can be expressed as a linear combination of $k$ factor returns, $r_{a} = μ_{a} + F r_{f} + ε_{a}$ , where $k ≪ p$ . In the mean-variance framework, portfolio risk is

$Var (R_{p}) = Var ({r_{a}}^{T} w_{a}) = Var ({(μ_{a} + F r_{f} + ε_{a})}^{T} w_{a}) = w_{a}^{T} (F Σ_{f} F^{T} + D) w_{a}$ ,

where:

$R_{p}$ is the portfolio return (a scalar).
$r_{a}$ is the asset returns.
$μ_{a}$ is the mean of asset returns.
$F$ is the factor loading, with dimension $n \times k$ .
$r_{f}$ is the factor return.
$ε_{a}$ is the idiosyncratic return related to each asset.
$w_{a}$ is the asset weight.
$Σ_{f}$ is the covariance of factor returns.
$D$ is the variance of idiosyncratic returns.

The parameters $r_{a}$ , $w_{a}$ , $μ_{a}$ and $ε_{a}$ are $n \times 1$ column vectors, $r_{f}$ and $w_{f}$ are $k \times 1$ column vectors, and $Σ_{k}$ and $D$ are a $k \times k$ and a $n \times n$ matrices, respectively.

Therefore, the mean-variance optimization problem is formulated as

$\begin{array}{l} \max_{w_{a}} μ_{a}^{T} w_{a} \\ s . t . w_{a}^{T} (F Σ_{f} F^{T} + D) w_{a} \leq τ, \\ \sum_{a \in A} w_{a} = 1, \\ 0 \leq w_{a} \leq 1 . \end{array}$

In the dimensional space formed by $n$ asset returns, PCA finds the $k$ directions that capture the most important variations in the returns. Usually, $k$ is less than $n$ . Therefore, by using PCA, you can decompose the $n$ asset returns into $k$ directions that are interpreted as factor loadings. The scores from the decomposition are interpreted as the factor returns. For more information, see pca (Statistics and Machine Learning Toolbox™). In this example, the factor model uses $k =$ nFactors, where covarianceDenoising determines the numFactors.

Compute the maximum return portfolio subject to a target risk of 0.008 using the factor model covariance estimate. For details on how to obtain the weights allocation using factor modeling, see Portfolio Optimization Using Factor Models.

% Compute weights with denoised strategy
userData.numFactors = [];
[wFactorModel_initial,userData] = factorModeling(w0,warmupTT, ...
    userData);

Check for asset allocations that are over 5% to show assets with large investment weights.

percentage = 0.05;
AssetName = pricesTT.Properties.VariableNames( ...
    wFactorModel_initial>=percentage)';
Weight = wFactorModel_initial(wFactorModel_initial>=percentage);
T2 = table(AssetName,Weight)

T2=6×2 table
     AssetName      Weight 
    ___________    ________

    {'Asset6' }    0.075366
    {'Asset35'}    0.069395
    {'Asset47'}     0.10676
    {'Asset50'}     0.21628
    {'Asset75'}     0.12423
    {'Asset94'}      0.3068

The assets with large investment weights are almost the same for both investment strategies. Asset35 is the only asset that appears in one table, namely in the factor model strategy, and not the other. Even the weights of the assets are similar.

Backtesting

Use backtestStrategy to create strategy objects for the two investment strategies. Compare the denoising strategy (strat1) against the factor model strategy (strat2) using backtesting.

% Rebalance approximately every month
rebalFreq = 21;

% Set the rolling lookback window to be at least 2 months and at
% most 6 months
lookback  = [42 126];

% Use a fixed transaction cost (buy and sell costs are both 0.5%
% of amount traded)
transactionsFixed = 0.005;

% Strategies
strat1 = backtestStrategy('Factor Modeling', @factorModeling, ...
    UserData=userData, ...
    RebalanceFrequency=rebalFreq, ...
    LookbackWindow=lookback, ...
    TransactionCosts=transactionsFixed, ...
    InitialWeights=wFactorModel_initial);

strat2 = backtestStrategy('Denoising', @denoising, ...
    RebalanceFrequency=rebalFreq, ...
    LookbackWindow=lookback, ...
    TransactionCosts=transactionsFixed, ...
    InitialWeights=wDenoised_initial);

% Aggregate the strategy objects into an array
strategies = [strat1, strat2];

Create a backtestEngine object for the strategies, run the backtest using runBacktest, and generate a report using summary.

% Create the backtesting engine object
backtester = backtestEngine(strategies);

% Run backtest
backtester = runBacktest(backtester,pricesTT,'Start',warmupPeriod);

% Generate summary table of strategies performance
summary(backtester)

ans=9×2 table
                       Factor_Modeling    Denoising 
                       _______________    __________

    TotalReturn             0.28079          0.31501
    SharpeRatio            0.018583         0.020462
    Volatility            0.0089592        0.0086696
    AverageTurnover        0.014646         0.013843
    MaxTurnover             0.56184          0.58224
    AverageReturn        0.00016644       0.00017736
    MaxDrawdown             0.23384          0.24536
    AverageBuyCost          0.84446          0.79536
    AverageSellCost         0.84446          0.79536

Use equityCurve to plot the equity curve to compare the performance of both strategies.

equityCurve(backtester)

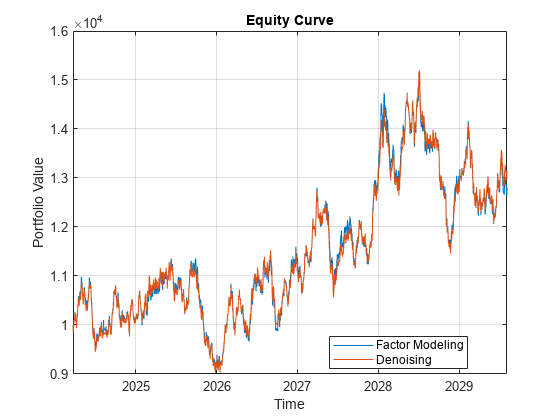
Figure contains an axes object. The axes object with title Equity Curve, xlabel Time, ylabel Portfolio Value contains 2 objects of type line. These objects represent Factor Modeling, Denoising.

The performance of both strategies is similar, although not identical. This similarity is because the factor model strategy uses the number of factors identified by covarianceDenoising to select the number of principal components. Factor model strategies are usually not implemented this way, but rather the number of factors is a fixed parameter that is chosen a priori.

In this example, the number of factors that is most frequently identified is 1.

% Count the number of different factors
categoricalNumFactors = ...
    categorical(backtester.Strategies(1).UserData.numFactors);
[N,uniqueFactors] = histcounts(categoricalNumFactors);
factorFrequency = table(uniqueFactors',N', ...
    'VariableNames',{'NumFactors','Frequency'})

factorFrequency=3×2 table
    NumFactors    Frequency
    __________    _________

      {'1' }         81    
      {'2' }         12    
      {'17'}          1

Therefore, you can run the factor modeling strategy using 1 as the number of factors instead of using covarianceDenoising to identify the number of factors at each rebalancing period.

Reference

Meucci, Attilio. “Modeling the Market.” In Risk and Asset Allocation, by Attilio Meucci, 101–66. Berlin, Heidelberg: Springer Berlin Heidelberg, 2009.

Local Functions

function [new_weights,userData] =...
    factorModeling(~,pricesTT,userData)
% Compute minimum variance portfolio using traditional covariance estimate.

% Compute returns from prices timetable.
assetReturns = tick2ret(pricesTT);

% Compute the number of factors identified using covariance denoising.
[~,numFactors] = covarianceDenoising(assetReturns.Variables);
userData.numFactors = [userData.numFactors; numFactors];

% Compute the covariance using the factors model
%   SigmaFactorModel = F*Sigma_f*F' + D
%   r_a = mu_a + F*r_f + epsilon_a
[factorLoading,factorRetn,~,~,~,factorMean] = ...
    pca(assetReturns.Variables,'NumComponents',numFactors);
covFactor = cov(factorRetn);
retnHat = factorRetn*factorLoading' + factorMean;
unexplainedRetn = assetReturns.Variables - retnHat;
unexplainedCovar = diag(cov(unexplainedRetn));
D = diag(unexplainedCovar);

% Define the mean and covariance of the returns.
mu = mean(assetReturns.Variables);
Sigma = factorLoading*covFactor*factorLoading' + D;

% Create the portfolio problem.
p = Portfolio(AssetMean=mu,AssetCovar=Sigma);
% Specify long-only, fully-invested contraints
p = setDefaultConstraints(p);

% Compute the maximum return portfolio subject to the target risk.
targetRisk = 0.008;
new_weights = estimateFrontierByRisk(p,targetRisk);
end

function new_weights = denoising(~, pricesTT) 
% Compute minimum variance portfolio using covariance denoising.

% Compute the returns from the prices timetable.
assetReturns = tick2ret(pricesTT);
mu = mean(assetReturns.Variables);
Sigma = covarianceDenoising(assetReturns.Variables);

% Create the portfolio problem.
p = Portfolio(AssetMean=mu,AssetCovar=Sigma);
% Long-only fully invested contraints
p = setDefaultConstraints(p);

% Compute maximum return portfolio subject to the target risk.
targetRisk = 0.008;
new_weights = estimateFrontierByRisk(p,targetRisk);
end

Related Examples

Portfolio Optimization Against a Benchmark

More About

Comparison of Methods for Covariance Estimation