estimateFrontier

估计有效边界上指定数量的最优投资组合

全页折叠

语法

[pwgt,pbuy,psell] = estimateFrontier(obj)
[pwgt,pbuy,psell] = estimateFrontier(obj,NumPorts)

说明

[pwgt,pbuy,psell] = estimateFrontier(obj) 基于 Portfolio、PortfolioCVaR 或 PortfolioMAD 对象估计有效边界上指定数量的最优投资组合。有关使用这些不同对象时各自工作流的详细信息，请参阅 Portfolio 对象工作流、PortfolioCVaR 对象工作流和 PortfolioMAD 对象工作流。

示例

[pwgt,pbuy,psell] = estimateFrontier(obj,NumPorts) 还指定一个额外选项 NumPorts 来估计有效边界上指定数量的最优投资组合。

示例

示例

全部折叠

打开实时脚本

创建有效投资组合： 

load CAPMuniverse

p = Portfolio('AssetList',Assets(1:12));
p = estimateAssetMoments(p, Data(:,1:12),'missingdata',true);
p = setDefaultConstraints(p);
plotFrontier(p);

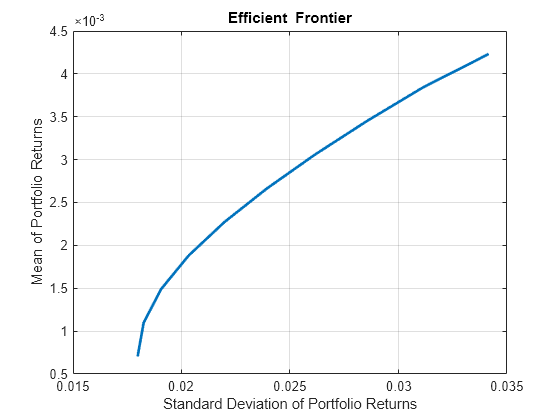
Figure contains an axes object. The axes object with title Efficient Frontier, xlabel Standard Deviation of Portfolio Returns, ylabel Mean of Portfolio Returns contains an object of type line. This object represents Efficient Frontier.

pwgt = estimateFrontier(p, 5);

pnames = cell(1,5);
for i = 1:5
	pnames{i} = sprintf('Port%d',i);
end

Blotter = dataset([{pwgt},pnames],'obsnames',p.AssetList);

disp(Blotter);
            Port1        Port2       Port3       Port4      Port5
    AAPL     0.017926    0.058247    0.097816    0.12955    0    
    AMZN            0           0           0          0    0    
    CSCO            0           0           0          0    0    
    DELL    0.0041906           0           0          0    0    
    EBAY            0           0           0          0    0    
    GOOG      0.16144     0.35678     0.55228    0.75116    1    
    HPQ      0.052566    0.032302    0.011186          0    0    
    IBM       0.46422     0.36045     0.25577    0.11928    0    
    INTC            0           0           0          0    0    
    MSFT      0.29966     0.19222    0.082949          0    0    
    ORCL            0           0           0          0    0    
    YHOO            0           0           0          0    0
打开实时脚本

根据 CAPMuniverse.mat 为 12 支股票创建一个 Portfolio 对象。 

load CAPMuniverse
p0 = Portfolio('AssetList',Assets(1:12));
p0 = estimateAssetMoments(p0, Data(:,1:12),'missingdata',true);
p0 = setDefaultConstraints(p0);

使用 setMinMaxNumAssets 定义最多 3 项资产。

p1 = setMinMaxNumAssets(p0, [], 3);

使用 setBounds 定义下限、上限和为 'Conditional' 的 BoundType。

p1 = setBounds(p1, 0.1, 0.5,'BoundType', 'Conditional');
pwgt = estimateFrontier(p1, 5);

下表显示，优化后的配置只投资了最多 3 项资产，并避免了小于 0.1 的小头寸。

result = table(p0.AssetList', pwgt)
result=12×2 table
      Var1                                     pwgt                                
    ________    ___________________________________________________________________

    {'AAPL'}          0              0              0        0.14232              0
    {'AMZN'}          0              0              0              0              0
    {'CSCO'}          0              0              0              0              0
    {'DELL'}          0              0              0              0              0
    {'EBAY'}          0              0              0              0            0.5
    {'GOOG'}    0.16891        0.29534        0.42177            0.5            0.5
    {'HPQ' }          0              0      4.996e-15    -2.7756e-17              0
    {'IBM' }    0.49968        0.43657        0.37326        0.35768              0
    {'INTC'}          0              0              0              0              0
    {'MSFT'}     0.3314         0.2681        0.20496     4.6838e-17              0
    {'ORCL'}          0              0              0              0              0
    {'YHOO'}          0              0              0              0              0

estimateFrontier 函数使用 MINLP 求解器来求解此问题。使用 setSolverMINLP 函数来配置 SolverType 和选项。

p1.solverTypeMINLP
ans = 
'OuterApproximation'

p1.solverOptionsMINLP
ans = struct with fields:
                           MaxIterations: 1000
                    AbsoluteGapTolerance: 1.0000e-07
                    RelativeGapTolerance: 1.0000e-05
                  NonlinearScalingFactor: 1000
                  ObjectiveScalingFactor: 1000
                                 Display: 'off'
                           CutGeneration: 'basic'
                MaxIterationsInactiveCut: 30
                      ActiveCutTolerance: 1.0000e-07
                    IntMainSolverOptions: [1×1 optim.options.Intlinprog]
    NumIterationsEarlyIntegerConvergence: 30
                     ExtendedFormulation: 0
                            NumInnerCuts: 10
                     NumInitialOuterCuts: 10
打开实时脚本

创建有效投资组合： 

load CAPMuniverse

p = PortfolioCVaR('AssetList',Assets(1:12));
p = simulateNormalScenariosByData(p, Data(:,1:12), 20000 ,'missingdata',true);
p = setDefaultConstraints(p);
p = setProbabilityLevel(p, 0.95);

plotFrontier(p);

Figure contains an axes object. The axes object with title Efficient Frontier, xlabel Conditional Value-at-Risk of Portfolio, ylabel Mean of Portfolio Returns contains an object of type line. This object represents Efficient Frontier.

pwgt = estimateFrontier(p, 5);

pnames = cell(1,5);
for i = 1:5
	pnames{i} = sprintf('Port%d',i);
end

Blotter = dataset([{pwgt},pnames],'obsnames',p.AssetList);

disp(Blotter);
            Port1       Port2       Port3       Port4      Port5
    AAPL    0.010223    0.073393     0.11939    0.13137    0    
    AMZN           0           0           0          0    0    
    CSCO           0           0           0          0    0    
    DELL     0.02301           0           0          0    0    
    EBAY           0           0           0          0    0    
    GOOG     0.20389     0.38068     0.56253    0.75919    1    
    HPQ     0.041396    0.009472           0          0    0    
    IBM      0.44369     0.36472     0.26247    0.10944    0    
    INTC           0           0           0          0    0    
    MSFT     0.27779     0.17174    0.055611          0    0    
    ORCL           0           0           0          0    0    
    YHOO           0           0           0          0    0
打开实时脚本

创建有效投资组合： 

load CAPMuniverse

p = PortfolioMAD('AssetList',Assets(1:12));
p = simulateNormalScenariosByData(p, Data(:,1:12), 20000 ,'missingdata',true);
p = setDefaultConstraints(p);

plotFrontier(p);

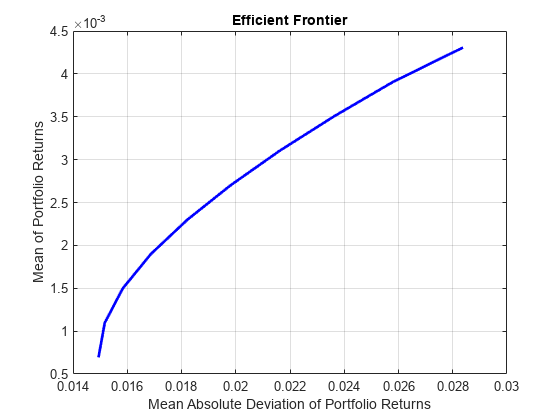
Figure contains an axes object. The axes object with title Efficient Frontier, xlabel Mean Absolute Deviation of Portfolio Returns, ylabel Mean of Portfolio Returns contains an object of type line. This object represents Efficient Frontier.

pwgt = estimateFrontier(p, 5);

pnames = cell(1,5);
for i = 1:5
	pnames{i} = sprintf('Port%d',i);
end

Blotter = dataset([{pwgt},pnames],'obsnames',p.AssetList);

disp(Blotter);
            Port1        Port2       Port3       Port4      Port5
    AAPL     0.029643    0.075874     0.11335    0.13405    0    
    AMZN            0           0           0          0    0    
    CSCO            0           0           0          0    0    
    DELL    0.0086367           0           0          0    0    
    EBAY            0           0           0          0    0    
    GOOG      0.16177     0.35217     0.54489    0.74913    1    
    HPQ      0.056891    0.023419           0          0    0    
    IBM       0.45916     0.37921     0.29376    0.11682    0    
    INTC            0           0           0          0    0    
    MSFT       0.2839     0.16933    0.048005          0    0    
    ORCL            0           0           0          0    0    
    YHOO            0           0           0          0    0
打开实时脚本

获得整个有效边界范围上的默认有效投资组合数量。 

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];

p = Portfolio;
p = setAssetMoments(p, m, C);
p = setDefaultConstraints(p);
pwgt = estimateFrontier(p);
disp(pwgt);
    0.8891    0.7215    0.5540    0.3865    0.2190    0.0515         0         0         0         0
    0.0369    0.1289    0.2209    0.3129    0.4049    0.4969    0.4049    0.2314    0.0579         0
    0.0404    0.0567    0.0730    0.0893    0.1056    0.1219    0.1320    0.1394    0.1468         0
    0.0336    0.0929    0.1521    0.2113    0.2705    0.3297    0.4630    0.6292    0.7953    1.0000
打开实时脚本

从初始投资组合开始，estimateFrontier 函数返回从您的初始投资组合到有效边界上每个有效投资组合的买入交易和卖出交易。给定 pwgt0 中的初始投资组合，您可以得到买入交易和卖出交易。 

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
      0.00408 0.0289 0.0204 0.0119;
      0.00192 0.0204 0.0576 0.0336;
      0 0.0119 0.0336 0.1225 ];
 
p = Portfolio;
p = setAssetMoments(p, m, C);
p = setDefaultConstraints(p);
pwgt0 = [ 0.3; 0.3; 0.2; 0.1 ];
p = setInitPort(p, pwgt0);
[pwgt, pbuy, psell] = estimateFrontier(p);

display(pwgt);
pwgt = 4×10

    0.8891    0.7215    0.5540    0.3865    0.2190    0.0515         0         0         0         0
    0.0369    0.1289    0.2209    0.3129    0.4049    0.4969    0.4049    0.2314    0.0579         0
    0.0404    0.0567    0.0730    0.0893    0.1056    0.1219    0.1320    0.1394    0.1468         0
    0.0336    0.0929    0.1521    0.2113    0.2705    0.3297    0.4630    0.6292    0.7953    1.0000


display(pbuy);
pbuy = 4×10

    0.5891    0.4215    0.2540    0.0865         0         0         0         0         0         0
         0         0         0    0.0129    0.1049    0.1969    0.1049         0         0         0
         0         0         0         0         0         0         0         0         0         0
         0         0    0.0521    0.1113    0.1705    0.2297    0.3630    0.5292    0.6953    0.9000


display(psell);
psell = 4×10

         0         0         0         0    0.0810    0.2485    0.3000    0.3000    0.3000    0.3000
    0.2631    0.1711    0.0791         0         0         0         0    0.0686    0.2421    0.3000
    0.1596    0.1433    0.1270    0.1107    0.0944    0.0781    0.0680    0.0606    0.0532    0.2000
    0.0664    0.0071         0         0         0         0         0         0         0         0
打开实时脚本

获得整个有效边界范围上的默认有效投资组合数量。 

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;

rng(11);

AssetScenarios = mvnrnd(m, C, 20000);

p = PortfolioCVaR;
p = setScenarios(p, AssetScenarios);
p = setDefaultConstraints(p);
p = setProbabilityLevel(p, 0.95);

pwgt = estimateFrontier(p);

disp(pwgt);
    0.8445    0.6841    0.5148    0.3534    0.1897    0.0303         0         0         0         0
    0.0609    0.1429    0.2302    0.3171    0.3987    0.4742    0.3524    0.1803         0         0
    0.0458    0.0640    0.0945    0.1081    0.1340    0.1590    0.1738    0.1918    0.2211         0
    0.0488    0.1090    0.1606    0.2215    0.2776    0.3365    0.4738    0.6280    0.7789    1.0000

函数 rng(seed) 重置了随机数生成器以得到文档中的结果。在模拟场景时重置随机数生成器这一步并不是必需的。

打开实时脚本

从初始投资组合开始，estimateFrontier 函数返回从您的初始投资组合到有效边界上每个有效投资组合的买入交易和卖出交易。给定 pwgt0 中的初始投资组合，您可以得到买入交易和卖出交易。 

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;

rng(11);

AssetScenarios = mvnrnd(m, C, 20000);
p = PortfolioCVaR;
p = setScenarios(p, AssetScenarios);
p = setDefaultConstraints(p);
p = setProbabilityLevel(p, 0.95);

pwgt0 = [ 0.3; 0.3; 0.2; 0.1 ];
p = setInitPort(p, pwgt0);
[pwgt, pbuy, psell] = estimateFrontier(p);

display(pwgt);
pwgt = 4×10

    0.8445    0.6841    0.5148    0.3534    0.1897    0.0303         0         0         0         0
    0.0609    0.1429    0.2302    0.3171    0.3987    0.4742    0.3524    0.1803         0         0
    0.0458    0.0640    0.0945    0.1081    0.1340    0.1590    0.1738    0.1918    0.2211         0
    0.0488    0.1090    0.1606    0.2215    0.2776    0.3365    0.4738    0.6280    0.7789    1.0000


display(pbuy);
pbuy = 4×10

    0.5445    0.3841    0.2148    0.0534         0         0         0         0         0         0
         0         0         0    0.0171    0.0987    0.1742    0.0524         0         0         0
         0         0         0         0         0         0         0         0    0.0211         0
         0    0.0090    0.0606    0.1215    0.1776    0.2365    0.3738    0.5280    0.6789    0.9000


display(psell);
psell = 4×10

         0         0         0         0    0.1103    0.2697    0.3000    0.3000    0.3000    0.3000
    0.2391    0.1571    0.0698         0         0         0         0    0.1197    0.3000    0.3000
    0.1542    0.1360    0.1055    0.0919    0.0660    0.0410    0.0262    0.0082         0    0.2000
    0.0512         0         0         0         0         0         0         0         0         0

函数 rng(seed) 重置了随机数生成器以得到文档中的结果。在模拟场景时重置随机数生成器这一步并不是必需的。

打开实时脚本

获得整个有效边界范围上的默认有效投资组合数量。 

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;

rng(11);

AssetScenarios = mvnrnd(m, C, 20000);

p = PortfolioMAD;
p = setScenarios(p, AssetScenarios);
p = setDefaultConstraints(p);

pwgt = estimateFrontier(p);

disp(pwgt);
    0.8817    0.7150    0.5488    0.3811    0.2173    0.0503         0         0         0         0
    0.0435    0.1290    0.2130    0.2987    0.3821    0.4668    0.3614    0.1751         0         0
    0.0385    0.0600    0.0826    0.1061    0.1242    0.1477    0.1780    0.2101    0.2267         0
    0.0363    0.0960    0.1556    0.2141    0.2764    0.3352    0.4605    0.6148    0.7733    1.0000

函数 rng(seed) 重置了随机数生成器以得到文档中的结果。在模拟场景时重置随机数生成器这一步并不是必需的。

打开实时脚本

从初始投资组合开始，estimateFrontier 函数返回从您的初始投资组合到有效边界上每个有效投资组合的买入交易和卖出交易。给定 pwgt0 中的初始投资组合，您可以得到买入交易和卖出交易。 

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;

rng(11);

AssetScenarios = mvnrnd(m, C, 20000);
p = PortfolioMAD;
p = setScenarios(p, AssetScenarios);
p = setDefaultConstraints(p);

pwgt0 = [ 0.3; 0.3; 0.2; 0.1 ];
p = setInitPort(p, pwgt0);
[pwgt, pbuy, psell] = estimateFrontier(p);

display(pwgt);
pwgt = 4×10

    0.8817    0.7150    0.5488    0.3811    0.2173    0.0503         0         0         0         0
    0.0435    0.1290    0.2130    0.2987    0.3821    0.4668    0.3614    0.1751         0         0
    0.0385    0.0600    0.0826    0.1061    0.1242    0.1477    0.1780    0.2101    0.2267         0
    0.0363    0.0960    0.1556    0.2141    0.2764    0.3352    0.4605    0.6148    0.7733    1.0000


display(pbuy);
pbuy = 4×10

    0.5817    0.4150    0.2488    0.0811         0         0         0         0         0         0
         0         0         0         0    0.0821    0.1668    0.0614         0         0         0
         0         0         0         0         0         0         0    0.0101    0.0267         0
         0         0    0.0556    0.1141    0.1764    0.2352    0.3605    0.5148    0.6733    0.9000


display(psell);
psell = 4×10

         0         0         0         0    0.0827    0.2497    0.3000    0.3000    0.3000    0.3000
    0.2565    0.1710    0.0870    0.0013         0         0         0    0.1249    0.3000    0.3000
    0.1615    0.1400    0.1174    0.0939    0.0758    0.0523    0.0220         0         0    0.2000
    0.0637    0.0040         0         0         0         0         0         0         0         0

函数 rng(seed) 重置了随机数生成器以得到文档中的结果。在模拟场景时重置随机数生成器这一步并不是必需的。

输入参数

全部折叠

投资组合对象，使用 Portfolio、PortfolioCVaR 或 PortfolioMAD 对象指定。有关创建 Portfolio 对象的详细信息，请参阅

数据类型: object

要在有效边界上获得的点数，指定为整数标量。

注意

如果没有为 NumPorts 指定任何值，则从隐藏属性 defaultNumPorts 获得默认值（默认值为 10）。如果 NumPorts = 1，则此函数返回隐藏属性 defaultFrontierLimit 指定的投资组合（当前默认值为 'min'）。

数据类型: double

输出参量

全部折叠

有效边界上指定数量的最优投资组合，按从最小到最大的投资组合收益等间距分布，以 NumAssets×NumPorts 的矩阵形式返回。 为 Portfolio、PortfolioCVaR 或 PortfolioMAD 输入对象 (obj) 返回 pwgt。

为建立有效边界上的最优投资组合，相对于初始投资组合需要进行的买入交易，以 NumAssets×NumPorts 矩阵形式返回。

注意

如果没有在 obj.InitPort 中指定初始投资组合，则假定该值为 0，以便 pbuy = max(0, pwgt) 且 psell = max(0, -pwgt)。

对于 Portfolio、PortfolioCVaR 或 PortfolioMAD 输入对象 (obj)，返回 pbuy。

为建立有效边界上的最优投资组合，相对于初始投资组合需要进行的卖出交易，以 NumAssets×NumPorts 矩阵形式返回。

注意

如果没有在 obj.InitPort 中指定初始投资组合，则假定该值为 0，以便 pbuy = max(0, pwgt) 且 psell = max(0, -pwgt)。

为 Portfolio、PortfolioCVaR 或 PortfolioMAD 输入对象 (obj) 返回 psell。

详细信息

全部折叠

提示

  • 您还可以使用圆点表示法来估计整个有效边界上指定数量的最优投资组合。

     	[pwgt, pbuy, psell] = obj.estimateFrontier(NumPorts);

  • 向 Portfolio、PortfolioCVaR 或 PortfolioMAD 对象引入交易成本和周转约束后，投资组合优化目标会包含一个绝对值项。有关 Financial Toolbox™ 如何通过算法处理这类情况的详细信息，请参阅参考。

参考

[1] Cornuejols, G., and R. Tutuncu. Optimization Methods in Finance. Cambridge University Press, 2007.

版本历史记录

在 R2011a 中推出

另请参阅

| | | |

主题