使用 Financial Toolbox 的投资组合优化示例
通过一组示例来了解 Portfolio 对象的主要功能。具体来说，这些示例使用 Portfolio 对象来展示如何设置重点关注两基金分离定理、交易成本和换手率约束影响的均值-方差投资组合优化问题，如何获取最大化夏普比率的投资组合，以及如何建立两种流行的对冲基金策略（美元中性和 130/30 投资组合）。
设置数据
每个示例都对一个包含 30 支蓝筹股的股票池的月总收益矩进行处理。虽然这些数据从实际数据得来，但并不代表特定的资产或市场表现，仅供说明之用。数据包含在文件 BlueChipStockMoments.mat 中；在该文件中，资产标识符列表显示在 AssetList 变量中，资产收益的均值和方差分别显示在 AssetMean 和 AssetCovar 变量中，现金收益的均值和方差以及市场收益的均值和方差分别显示在 CashMean、CashVar、MarketMean 和 MarketVar 变量中。由于大多数分析要求使用资产收益的标准差作为风险代理，因此将现金和市场收益的方差转换为标准差。
load BlueChipStockMoments
mret = MarketMean;
mrsk = sqrt(MarketVar);
cret = CashMean;
crsk = sqrt(CashVar);创建 Portfolio 对象
首先，使用 Portfolio 创建一个标准 Portfolio 对象，以将资产列表、无风险利率和资产收益矩纳入该对象中。
p = Portfolio('AssetList',AssetList,'RiskFreeRate',CashMean); p = setAssetMoments(p,AssetMean,AssetCovar);
为了提供一个比较的基础，需建立一个等权重投资组合，并将其设为 Portfolio 对象中的初始投资组合。请记住，稍后要构造的对冲投资组合将需要一个不同的初始投资组合。创建初始投资组合后，estimatePortMoments 函数会估计等权重投资组合收益的均值和标准差。
p = setInitPort(p,1/p.NumAssets); [ersk,eret] = estimatePortMoments(p,p.InitPort);
通过专用的辅助函数 portfolioexamples_plot，可以绘制要在这里生成的所有结果。第一个绘图根据单个资产收益的均值和标准差显示各资产的分布情况。此外，等权重投资组合、市场投资组合和现金投资组合都绘制在同一绘图上。请注意，portfolioexamples_plot 函数会将月总收益转换为年化总收益。
clf; portfolioexamples_plot('Asset Risks and Returns', ... {'scatter', mrsk, mret, {'Market'}}, ... {'scatter', crsk, cret, {'Cash'}}, ... {'scatter', ersk, eret, {'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
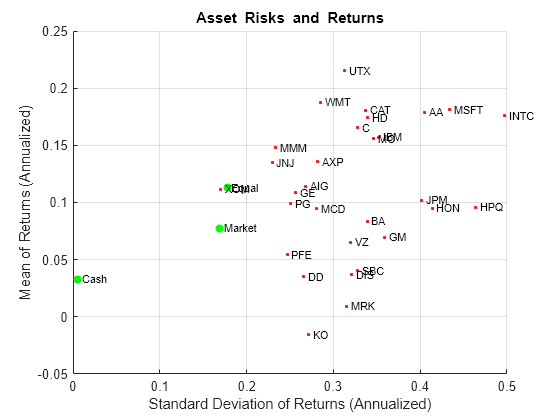
设置投资组合优化问题
使用 setDefaultConstraints 函数设置一个标准或默认的均值-方差投资组合优化问题，该函数要求满仓纯多头的投资组合（非负权重的总和必须为 1）。在给定此初始问题的情况下，使用 estimateFrontier 和 estimatePortMoments 函数估计有效边界，其中 estimateFrontier 估计有效投资组合，estimatePortMoments 估计这些投资组合的风险和收益。下一张图在之前的绘图上叠加了有效边界。
p = setDefaultConstraints(p); pwgt = estimateFrontier(p,20); [prsk,pret] = estimatePortMoments(p,pwgt); % Plot the efficient frontier. clf; portfolioexamples_plot('Efficient Frontier', ... {'line', prsk, pret}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
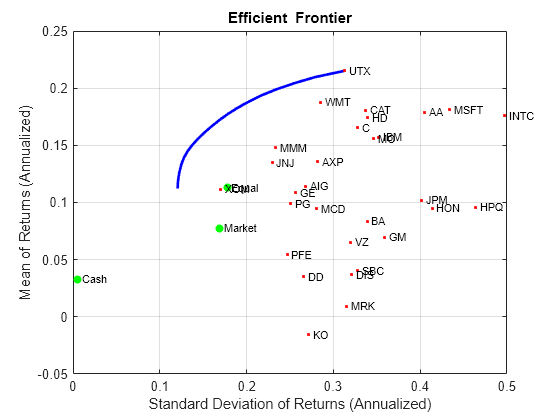
说明有效边界的切线
Tobin 的共同基金定理 (Tobin 1958) 指出，投资组合配置问题被视为在无风险资产和风险投资组合之间做出的一种配置决策。在均值-方差框架中，现金作为无风险资产的代理，有效边界上的一个有效投资组合作为风险投资组合，这样现金与该投资组合之间的任何配置都将主导有效边界上的所有其他投资组合。这一投资组合被称为切点投资组合，因为它是从无风险资产处开始向有效边界绘制的切线的切点。
在 Portfolio 对象已经具有无风险利率的情况下，通过创建 Portfolio 对象的副本来获取切线，该副本具有预算约束，允许 0% 到 100% 之间的现金配置。因为 Portfolio 对象是一个值对象，所以通过将 Portfolio 的输出或 "set" 函数分配给新的 Portfolio 对象实例，很容易就能创建一个副本。绘图显示了有效边界以及形成有效边界切线的 Tobin 配置。
q = setBudget(p, 0, 1); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); % Plot efficient frontier with tangent line (0 to 1 cash). clf; portfolioexamples_plot('Efficient Frontier with Tangent Line', ... {'line', prsk, pret}, ... {'line', qrsk, qret, [], [], 1}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
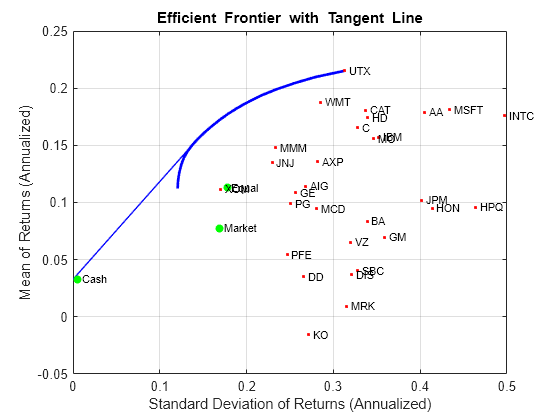
请注意，实际上现金也有一点儿小风险，因此切线并未穿过现金资产。
获取风险和收益范围
为了获取具有风险或收益目标值的有效投资组合，有必要获得有效边界上所有投资组合的风险和收益范围。这可以通过 estimateFrontierLimits 函数来实现。
[rsk,ret] = estimatePortMoments(p,estimateFrontierLimits(p)); display(rsk)
rsk = 2×1
0.0348
0.0903
display(ret)
ret = 2×1
0.0094
0.0179
月投资组合收益在 0.9% 到 1.8% 的范围内，投资组合风险在 3.5% 和 9.0% 的范围内。按年计算，投资组合收益在 11.2% 到 21.5% 的范围内，投资组合风险在 12.1% 到 31.3% 的范围内。
查找具有目标收益和目标风险的投资组合
在给定风险和收益范围的情况下，可以使用 estimateFrontierByReturn 和 estimateFrontierByRisk 函数在有效边界上找到具有目标收益和风险值的特定投资组合。
TargetReturn = 0.20; % Input target annualized return and risk here. TargetRisk = 0.15; % Obtain portfolios with targeted return and risk. awgt = estimateFrontierByReturn(p,TargetReturn/12); [arsk,aret] = estimatePortMoments(p,awgt); bwgt = estimateFrontierByRisk(p,TargetRisk/sqrt(12)); [brsk,bret] = estimatePortMoments(p,bwgt); % Plot efficient frontier with targeted portfolios. clf; portfolioexamples_plot('Efficient Frontier with Targeted Portfolios', ... {'line', prsk, pret}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', arsk, aret, {sprintf('%g%% Return',100*TargetReturn)}}, ... {'scatter', brsk, bret, {sprintf('%g%% Risk',100*TargetRisk)}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
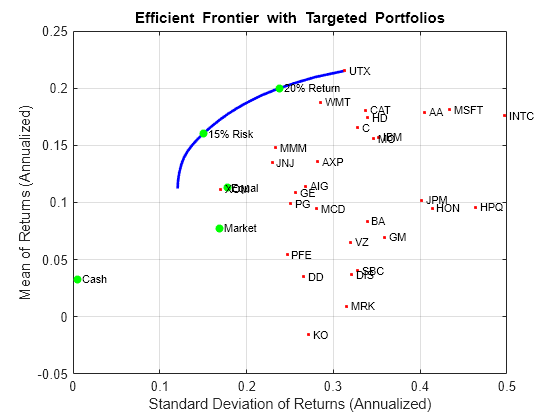
若要查看这些目标投资组合看起来怎么样，可使用 dataset 对象设置包含投资组合权重和资产名称（这些信息通过 Portfolio 对象获取）的“交易记事本”。
aBlotter = dataset({100*awgt(awgt > 0),'Weight'}, 'obsnames', p.AssetList(awgt > 0));
displayPortfolio(sprintf('Portfolio with %g%% Target Return', 100*TargetReturn), aBlotter, false);Portfolio with 20% Target Return
Weight
CAT 1.1445
INTC 0.17452
MO 9.6521
MSFT 0.85862
UTX 56.918
WMT 31.253
bBlotter = dataset({100*bwgt(bwgt > 0),'Weight'}, 'obsnames', p.AssetList(bwgt > 0));
displayPortfolio(sprintf('Portfolio with %g%% Target Risk', 100*TargetRisk), bBlotter, false);Portfolio with 15% Target Risk
Weight
AA 1.8565e-21
AIG 5.962e-21
AXP 1.1063e-20
CAT 1.9038e-20
DD 3.2518e-21
DIS 1.6003e-20
GE 9.607e-22
HPQ 2.4156e-21
IBM 5.8501e-21
INTC 2.2585
JNJ 9.2162
MMM 16.603
MO 15.388
MSFT 4.4467
PFE 3.4596e-21
PG 4.086
UTX 10.281
WMT 25.031
XOM 12.69
交易成本
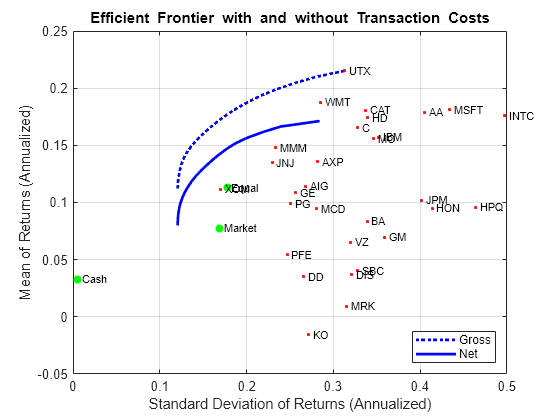
使用 Portfolio 对象可以将交易成本作为优化问题的一部分进行考虑。虽然可以为每个资产设置单独的成本，但使用 Portfolio 对象函数的标量扩展功能，可以为所有资产设置统一的交易成本，并将投资组合总收益和净收益两者的有效边界进行比较。
BuyCost = 0.0020; SellCost = 0.0020; q = setCosts(p,BuyCost,SellCost); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); % Plot efficient frontiers with gross and net returns. clf; portfolioexamples_plot('Efficient Frontier with and without Transaction Costs', ... {'line', prsk, pret, {'Gross'}, ':b'}, ... {'line', qrsk, qret, {'Net'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
换手率约束
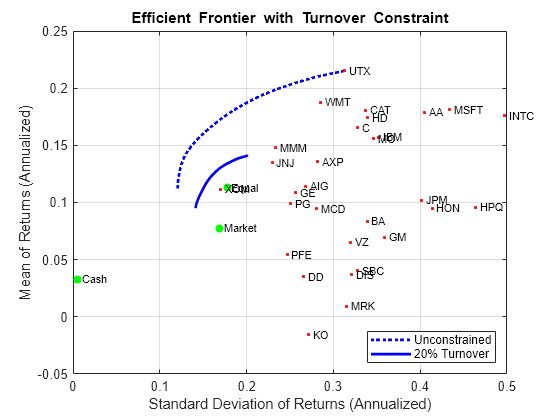
除了交易成本，Portfolio 对象还可以处理换手率约束。以下示例说明，施加换手率约束会在初始投资组合的邻域产生一个有效边界，这可能会限制交易。此外，引入换手率约束通常意味着，从初始投资组合转向无约束有效边界可能需要多次交易。因此，换手率约束引入了一种时间多样化形式，这种形式可以将交易分散到多个时间段。在此示例中，请注意，从 estimateFrontier 函数得出的买入交易和卖出交易的总和确认满足换手率约束。
BuyCost = 0.0020; SellCost = 0.0020; Turnover = 0.2; q = setCosts(p, BuyCost,SellCost); q = setTurnover(q,Turnover); [qwgt,qbuy,qsell] = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); % Plot efficient frontier with turnover constraint. clf; portfolioexamples_plot('Efficient Frontier with Turnover Constraint', ... {'line', prsk, pret, {'Unconstrained'}, ':b'}, ... {'line', qrsk, qret, {sprintf('%g%% Turnover', 100*Turnover)}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
displaySumOfTransactions(Turnover, qbuy, qsell)
Sum of Purchases by Portfolio along Efficient Frontier (Max. Turnover 20%) 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 Sum of Sales by Portfolio along Efficient Frontier (Max. Turnover 20%) 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000
跟踪误差约束
Portfolio 可以处理跟踪误差约束，其中跟踪误差是一个投资组合与跟踪投资组合相比的相对风险。在此示例中，包含九个资产的子集合形成了一个等权重跟踪投资组合。目标是找到跟踪误差在此跟踪投资组合的 5% 范围内的有效投资组合。
ii = [15, 16, 20, 21, 23, 25, 27, 29, 30]; % Indexes of assets to include in the tracking portfolio. TrackingError = 0.05/sqrt(12); TrackingPort = zeros(30, 1); TrackingPort(ii) = 1; TrackingPort = (1/sum(TrackingPort))*TrackingPort; q = setTrackingError(p,TrackingError,TrackingPort); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); [trsk,tret] = estimatePortMoments(q,TrackingPort); % Plot the efficient frontier with tracking-error constraint. clf; portfolioexamples_plot('Efficient Frontier with 5% Tracking-Error Constraint', ... {'line', prsk, pret, {'Unconstrained'}, ':b'}, ... {'line', qrsk, qret, {'Tracking'}}, ... {'scatter', [mrsk, crsk], [mret, cret], {'Market', 'Cash'}}, ... {'scatter', trsk, tret, {'Tracking'}, 'r'});
换手率和跟踪误差组合约束
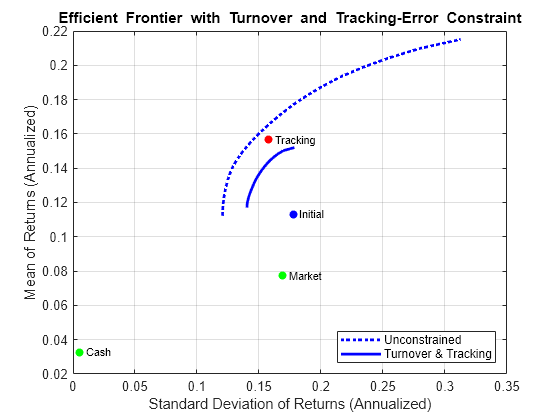
此示例说明了将不同约束组合应用时发生的交互效应。在这种情况下，必须同时满足相对于初始等权重投资组合的换手率约束和相对于跟踪投资组合的跟踪误差约束。换手率约束要求换手率不超过 30%，跟踪误差约束要求跟踪误差不超过 5%。请注意，从初始投资组合到跟踪投资组合的换手率为 70%，所以 30% 的换手率上界意味着有效边界将位于初始投资组合和跟踪投资组合之间的某个位置。
Turnover = 0.3; InitPort = (1/q.NumAssets)*ones(q.NumAssets, 1); ii = [15, 16, 20, 21, 23, 25, 27, 29, 30]; % Indexes of assets to include in tracking portfolio. TrackingError = 0.05/sqrt(12); TrackingPort = zeros(30, 1); TrackingPort(ii) = 1; TrackingPort = (1/sum(TrackingPort))*TrackingPort; q = setTurnover(q,Turnover,InitPort); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); [trsk,tret] = estimatePortMoments(q,TrackingPort); [ersk,eret] = estimatePortMoments(q,InitPort); % Plot the efficient frontier with combined turnover and tracking-error constraint. clf; portfolioexamples_plot('Efficient Frontier with Turnover and Tracking-Error Constraint', ... {'line', prsk, pret, {'Unconstrained'}, ':b'}, ... {'line', qrsk, qret, {'Turnover & Tracking'}}, ... {'scatter', [mrsk, crsk], [mret, cret], {'Market', 'Cash'}}, ... {'scatter', trsk, tret, {'Tracking'}, 'r'}, ... {'scatter', ersk, eret, {'Initial'}, 'b'});
最大化夏普比率
夏普比率 (Sharpe 1966) 是衡量收益与风险的一个测度，在投资组合分析中发挥着重要作用。具体说来，根据共同基金定理，最大化夏普比率的投资组合也就是有效边界上的切点投资组合。通过 estimateMaxSharpeRatio 函数得出有效边界上的最大夏普比率投资组合，再用 dataset 对象列出此投资组合中的资产。
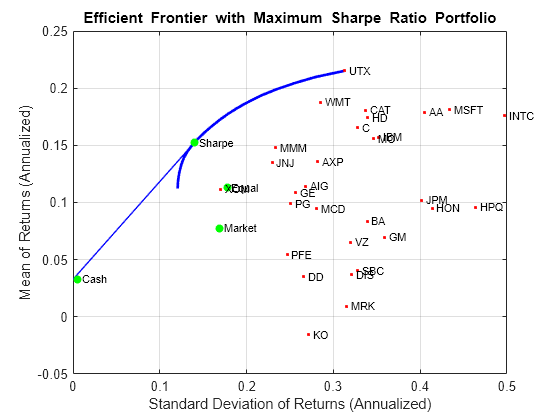
p = setInitPort(p, 0); swgt = estimateMaxSharpeRatio(p); [srsk,sret] = estimatePortMoments(p,swgt); % Plot the efficient frontier with portfolio that attains maximum Sharpe ratio. clf; portfolioexamples_plot('Efficient Frontier with Maximum Sharpe Ratio Portfolio', ... {'line', prsk, pret}, ... {'scatter', srsk, sret, {'Sharpe'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
% Set up a dataset object that contains the portfolio that maximizes the Sharpe ratio. Blotter = dataset({100*swgt(swgt > 0),'Weight'}, 'obsnames', AssetList(swgt > 0)); displayPortfolio('Portfolio with Maximum Sharpe Ratio', Blotter, false);
Portfolio with Maximum Sharpe Ratio
Weight
AA 1.9673e-15
AIG 1.9059e-15
AXP 1.0567e-15
BA 5.6012e-16
C 2.0055e-15
CAT 2.9715e-15
DD 3.1346e-16
DIS 5.9556e-16
GE 5.6143e-15
GM 7.3245e-16
HD 2.0342e-11
HON 3.309e-16
HPQ 2.0307e-15
IBM 8.8744e-15
INTC 2.6638
JNJ 9.0044
JPM 5.4025e-16
KO 2.4602e-16
MCD 8.7471e-16
MMM 15.502
MO 13.996
MRK 3.2239e-16
MSFT 4.4777
PFE 7.3425e-16
PG 7.4588
SBC 3.8329e-16
UTX 6.0056
VZ 3.9079e-16
WMT 22.051
XOM 18.841
确认最大夏普比率是最大值
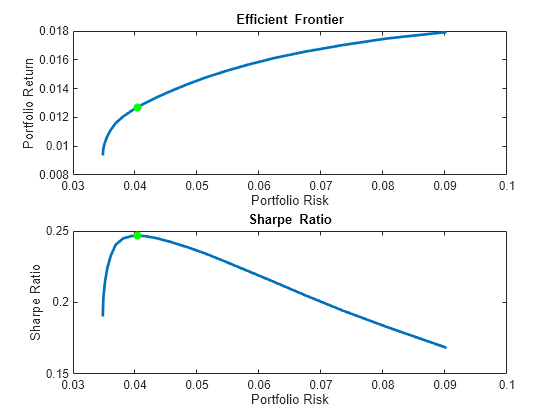
以下绘图说明了在有效边界上的所有投资组合中，此投资组合（用绘图上的点表示）的确最大化了夏普比率。
psratio = (pret - p.RiskFreeRate) ./ prsk; ssratio = (sret - p.RiskFreeRate) / srsk; clf; subplot(2,1,1); plot(prsk, pret, 'LineWidth', 2); hold on scatter(srsk, sret, 'g', 'filled'); title('\bfEfficient Frontier'); xlabel('Portfolio Risk'); ylabel('Portfolio Return'); hold off subplot(2,1,2); plot(prsk, psratio, 'LineWidth', 2); hold on scatter(srsk, ssratio, 'g', 'filled'); title('\bfSharpe Ratio'); xlabel('Portfolio Risk'); ylabel('Sharpe Ratio'); hold off
说明最大夏普比率投资组合是切点投资组合
下一个绘图说明了最大化夏普比率的投资组合也是切点投资组合（在这种情况下，预算约束被放开，允许 0% 到 100% 之间的现金配置）。
q = setBudget(p, 0, 1); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); % Plot showing that the Sharpe ratio portfolio is the tangency portfolio. clf; portfolioexamples_plot('Efficient Frontier with Maximum Sharpe Ratio Portfolio', ... {'line', prsk, pret}, ... {'line', qrsk, qret, [], [], 1}, ... {'scatter', srsk, sret, {'Sharpe'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
美元中性对冲基金结构
为了说明如何在对冲基金管理中使用投资组合优化工具，本文检验了两种流行的投资组合策略：美元中性投资组合和 130/30 投资组合策略。美元中性策略在多头头寸和空头头寸中进行等额投资，因此净投资组合头寸为 0。这样的投资组合被称为“美元中性”。
要建立美元中性投资组合，可从标准投资组合开始，并在 Exposure 变量中设置在多头头寸和空头头寸中的最大敞口。单个资产权重的边界为 ± Exposure。因为净头寸必须是美元中性，所以预算约束为 0，初始投资组合也必须为 0。最后，单向换手率约束提供了必要的多头和空头限制，以防止对多头头寸和空头头寸进行“双重计算”。交易记事本显示了使夏普比率最大化的美元中性投资组合的投资组合权重。多头头寸和空头头寸是从相对于初始投资组合的买入交易和卖出交易中获得的。
Exposure = 1; q = setBounds(p, -Exposure, Exposure); q = setBudget(q, 0, 0); q = setOneWayTurnover(q, Exposure, Exposure, 0); [qwgt,qlong,qshort] = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); [qswgt,qslong,qsshort] = estimateMaxSharpeRatio(q); [qsrsk,qsret] = estimatePortMoments(q,qswgt); % Plot the efficient frontier for a dollar-neutral fund structure with tangency portfolio. clf; portfolioexamples_plot('Efficient Frontier with Dollar-Neutral Portfolio', ... {'line', prsk, pret, {'Standard'}, 'b:'}, ... {'line', qrsk, qret, {'Dollar-Neutral'}, 'b'}, ... {'scatter', qsrsk, qsret, {'Sharpe'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
% Set up a dataset object that contains the portfolio that maximizes the Sharpe ratio. Blotter = dataset({100*qswgt(abs(qswgt) > 1.0e-4), 'Weight'}, ... {100*qslong(abs(qswgt) > 1.0e-4), 'Long'}, ... {100*qsshort(abs(qswgt) > 1.0e-4), 'Short'}, ... 'obsnames', AssetList(abs(qswgt) > 1.0e-4)); displayPortfolio('Dollar-Neutral Portfolio with Maximum Sharpe Ratio', Blotter, true, 'Dollar-Neutral');
Dollar-Neutral Portfolio with Maximum Sharpe Ratio
Weight Long Short
AA 0.5088 0.5088 0
AIG 3.0394 3.0394 0
AXP 0.92797 0.92797 0
BA -3.4952 0 3.4952
C 14.003 14.003 0
CAT 3.7261 3.7261 0
DD -18.063 0 18.063
DIS -4.8236 0 4.8236
GE -3.6178 0 3.6178
GM -3.7211 0 3.7211
HD 1.101 1.101 0
HON -1.4349 0 1.4349
HPQ 0.09909 0.09909 0
IBM -8.0585 0 8.0585
INTC 1.7693 1.7693 0
JNJ 1.3696 1.3696 0
JPM -2.5271 0 2.5271
KO -14.205 0 14.205
MCD 3.91 3.91 0
MMM 7.5995 7.5995 0
MO 4.0855 4.0855 0
MRK 3.747 3.747 0
MSFT 4.0769 4.0769 0
PFE -9.096 0 9.096
PG 1.6493 1.6493 0
SBC -5.2547 0 5.2547
UTX 5.7454 5.7454 0
VZ -2.438 0 2.438
WMT 0.84843 0.84843 0
XOM 18.529 18.529 0
Confirm Dollar-Neutral Portfolio
(Net, Long, Short)
0.0000 76.7350 76.7350
130/30 基金结构
最后，换手率约束用于设置 130/30 投资组合结构，这是一种净多头头寸的结构，但允许通过多头头寸和空头头寸在最大杠杆限度内加杠杆。在 130/30 投资组合的情况下，杠杆率为 30%。
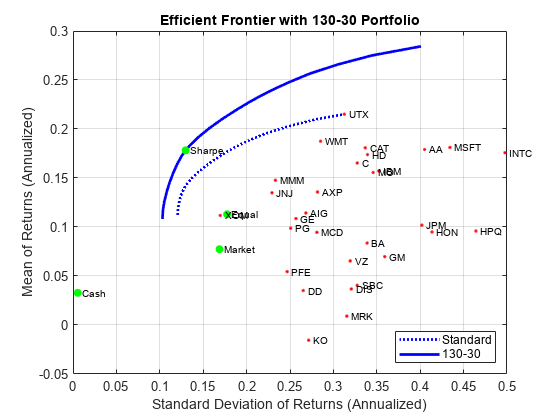
要建立 130/30 投资组合，可从标准投资组合问题开始，并在 Leverage 变量中设置杠杆率的最大值。单个资产权重的界限范围在 -Leverage 和 1 + Leverage 之间。因为净头寸必须是多头的，所以预算约束为 1，初始投资组合仍旧为 0。最后，单向换手率约束提供了必要的多头和空头限制，以防止对多头头寸和空头头寸进行“双重计算”。交易记事本显示了使夏普比率最大化的 130/30 投资组合的投资组合权重。多头头寸和空头头寸是从相对于初始投资组合的买入交易和卖出交易中获得的。
Leverage = 0.3; q = setBounds(p, -Leverage, 1 + Leverage); q = setBudget(q, 1, 1); q = setOneWayTurnover(q, 1 + Leverage, Leverage); [qwgt,qbuy,qsell] = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); [qswgt,qslong,qsshort] = estimateMaxSharpeRatio(q); [qsrsk,qsret] = estimatePortMoments(q,qswgt); % Plot the efficient frontier for a 130-30 fund structure with tangency portfolio. clf; portfolioexamples_plot(sprintf('Efficient Frontier with %g-%g Portfolio', ... 100*(1 + Leverage),100*Leverage), ... {'line', prsk, pret, {'Standard'}, 'b:'}, ... {'line', qrsk, qret, {'130-30'}, 'b'}, ... {'scatter', qsrsk, qsret, {'Sharpe'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
% Set up a dataset object that contains the portfolio that maximizes the Sharpe ratio. Blotter = dataset({100*qswgt(abs(qswgt) > 1.0e-4), 'Weight'}, ... {100*qslong(abs(qswgt) > 1.0e-4), 'Long'}, ... {100*qsshort(abs(qswgt) > 1.0e-4), 'Short'}, ... 'obsnames', AssetList(abs(qswgt) > 1.0e-4)); displayPortfolio(sprintf('%g-%g Portfolio with Maximum Sharpe Ratio', 100*(1 + Leverage), 100*Leverage), Blotter, true, sprintf('%g-%g', 100*(1 + Leverage), 100*Leverage));
130-30 Portfolio with Maximum Sharpe Ratio
Weight Long Short
DD -9.5565 0 9.5565
HON -6.0244 0 6.0244
INTC 4.0335 4.0335 0
JNJ 7.1234 7.1234 0
JPM -0.44583 0 0.44583
KO -13.646 0 13.646
MMM 20.908 20.908 0
MO 14.433 14.433 0
MSFT 4.5592 4.5592 0
PG 17.243 17.243 0
SBC -0.32712 0 0.32712
UTX 5.3584 5.3584 0
WMT 21.018 21.018 0
XOM 35.323 35.323 0
Confirm 130-30 Portfolio
(Net, Long, Short)
100.0000 130.0000 30.0000
参考资料
R. C. Grinold and R. N. Kahn.Active Portfolio Management.2nd ed.,2000.
H. M. Markowitz."Portfolio Selection."Journal of Finance.Vol. 1, No. 1, pp. 77-91, 1952.
J. Lintner."The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets."Review of Economics and Statistics.Vol. 47, No. 1, pp. 13-37, 1965.
H. M. Markowitz.Portfolio Selection:Efficient Diversification of Investments.John Wiley & Sons, Inc., 1959.
W. F. Sharpe."Mutual Fund Performance."Journal of Business.Vol. 39, No. 1, Part 2, pp. 119-138, 1966.
J. Tobin."Liquidity Preference as Behavior Towards Risk."Review of Economic Studies.Vol. 25, No.1, pp. 65-86, 1958.
J. L. Treynor and F. Black."How to Use Security Analysis to Improve Portfolio Selection."Journal of Business.Vol. 46, No. 1, pp. 68-86, 1973.
局部函数
function displaySumOfTransactions(Turnover, qbuy, qsell) fprintf('Sum of Purchases by Portfolio along Efficient Frontier (Max. Turnover %g%%)\n', ... 100*Turnover); fprintf('%.4f ', 100*sum(qbuy)), sprintf('\n\n'); fprintf('\n') fprintf('Sum of Sales by Portfolio along Efficient Frontier (Max. Turnover %g%%)\n', ... 100*Turnover); fprintf('%.4f ', 100*sum(qsell)); end function displayPortfolio(Description, Blotter, LongShortFlag, portfolioType) fprintf('%s\n', Description); disp(Blotter); if (LongShortFlag) fprintf('Confirm %s Portfolio\n', portfolioType); fprintf(' (Net, Long, Short)\n'); fprintf('%.4f ' , [ sum(Blotter.Weight), sum(Blotter.Long), sum(Blotter.Short) ]); end end
另请参阅
Portfolio | setBounds | addGroups | setAssetMoments | estimateAssetMoments | estimateBounds | plotFrontier | estimateFrontierLimits | estimateFrontierByRisk | estimatePortRisk
相关示例
- 创建 Portfolio 对象
- Working with Portfolio Constraints Using Defaults
- Validate the Portfolio Problem for Portfolio Object
- 估计 Portfolio 对象整个有效边界上的有效投资组合
- Estimate Efficient Frontiers for Portfolio Object
- 使用后处理结果设置可交易投资组合
- Portfolio Optimization with Semicontinuous and Cardinality Constraints
- Black-Litterman Portfolio Optimization Using Financial Toolbox
- Portfolio Optimization Against a Benchmark
- Asset Allocation Case Study
- Portfolio Analysis with Turnover Constraints
- Leverage in Portfolio Optimization with a Risk-Free Asset
- Black-Litterman Portfolio Optimization Using Financial Toolbox
- Portfolio Optimization Using Factor Models
- Portfolio Optimization Using Social Performance Measure
- Diversify Portfolios Using Custom Objective
详细信息
外部网站
You can also select a web site from the following list:
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)