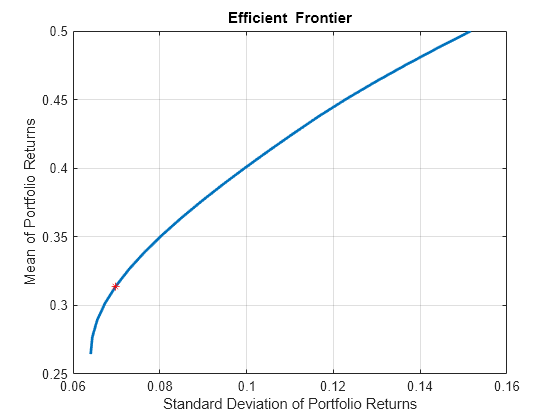
estimateMaxSharpeRatio
估计有效投资组合以最大化 Portfolio 对象的夏普比率
语法
说明
示例
估计使夏普比率最大化的有效投资组合。estimateMaxSharpeRatio 函数可使有效边界上的投资组合中的夏普比率最大化。此示例使用默认的 'direct' 方法估计最大夏普比率。有关 'direct 方法的详细信息，请参阅算法。
p = Portfolio('AssetMean',[0.3, 0.1, 0.5], 'AssetCovar',... [0.01, -0.010, 0.004; -0.010, 0.040, -0.002; 0.004, -0.002, 0.023]); p = setDefaultConstraints(p); plotFrontier(p, 20); weights = estimateMaxSharpeRatio(p); [risk, ret] = estimatePortMoments(p, weights); hold on plot(risk,ret,'*r');
估计使夏普比率最大化的有效投资组合。estimateMaxSharpeRatio 函数可使有效边界上的投资组合中的夏普比率最大化。此示例对未指定跟踪误差且仅使用线性约束的 Portfolio 对象 (p) 使用 'direct' 方法。setSolver 函数用于控制 SolverType 和 SolverOptions。在本例中，SolverType 为 quadprog。有关 'direct' 方法的详细信息，请参阅算法。
p = Portfolio('AssetMean',[0.3, 0.1, 0.5], 'AssetCovar',... [0.01, -0.010, 0.004; -0.010, 0.040, -0.002; 0.004, -0.002, 0.023]); p = setDefaultConstraints(p); plotFrontier(p, 20); p = setSolver(p,'quadprog','Display','off','ConstraintTolerance',1.0e-8,'OptimalityTolerance',1.0e-8,'StepTolerance',1.0e-8,'MaxIterations',10000); weights = estimateMaxSharpeRatio(p); [risk, ret] = estimatePortMoments(p, weights); hold on plot(risk,ret,'*r');
估计使夏普比率最大化的有效投资组合。estimateMaxSharpeRatio 函数可使有效边界上的投资组合中的夏普比率最大化。此示例对指定了跟踪误差且使用非线性约束的 Portfolio 对象 (p) 使用 'direct' 方法。setSolver 函数用于控制 SolverType 和 SolverOptions。在本例中，fmincon 为 SolverType。
p = Portfolio('AssetMean',[0.3, 0.1, 0.5], 'AssetCovar',... [0.01, -0.010, 0.004; -0.010, 0.040, -0.002; 0.004, -0.002, 0.023],'lb', 0,'budget', 1); plotFrontier(p, 20); p = setSolver(p, 'fmincon', 'Display', 'off', 'Algorithm', 'sqp', ... 'SpecifyObjectiveGradient', true, 'SpecifyConstraintGradient', true, ... 'ConstraintTolerance', 1.0e-8, 'OptimalityTolerance', 1.0e-8, 'StepTolerance', 1.0e-8); weights = estimateMaxSharpeRatio(p); te = 0.08; p = setTrackingError(p,te,weights); [risk, ret] = estimatePortMoments(p,weights); hold on plot(risk,ret,'*r');
estimateMaxSharpeRatio 函数可使有效边界上的投资组合中的夏普比率最大化。在具有无风险资产的投资组合的情况下，有多个有效的投资组合可以最大化资产线的夏普比率。鉴于 'direct' 和 'iterative' 方法自身的性质，上述每种方法的投资组合权重 (pwgts) 输出可能会有所不同，但夏普比率是相同的。此示例演示了 pwgts 不同而夏普比率相同的情形。
load BlueChipStockMoments mret = MarketMean; mrsk = sqrt(MarketVar); cret = CashMean; crsk = sqrt(CashVar); p = Portfolio('AssetList', AssetList, 'RiskFreeRate', CashMean); p = setAssetMoments(p, AssetMean, AssetCovar); p = setInitPort(p, 1/p.NumAssets); [ersk, eret] = estimatePortMoments(p, p.InitPort); p = setDefaultConstraints(p); pwgt = estimateFrontier(p, 20); [prsk, pret] = estimatePortMoments(p, pwgt); pwgtshpr_fully = estimateMaxSharpeRatio(p,'Method','direct'); [riskshpr_fully, retshpr_fully] = estimatePortMoments(p,pwgtshpr_fully); q = setBudget(p, 0, 1); qwgt = estimateFrontier(q, 20); [qrsk, qret] = estimatePortMoments(q, qwgt);
绘制有效边界及其切线（现金比例为 0 到 1）。
pwgtshpr_direct = estimateMaxSharpeRatio(q,'Method','direct'); pwgtshpr_iter = estimateMaxSharpeRatio(q,'Method','iterative'); % Default for 'TolX' is 1e-8 [riskshpr_diret, retshpr_diret] = estimatePortMoments(q,pwgtshpr_direct); [riskshpr_iter, retshpr_iter] = estimatePortMoments(q,pwgtshpr_iter); clf; portfolioexamples_plot('Efficient Frontier with Capital Allocation Line', ... {'line', prsk, pret, {'EF'}, '-r', 2}, ... {'line', qrsk, qret, {'EF with riskfree'}, '-b', 1}, ... {'scatter', [mrsk, crsk, ersk, riskshpr_fully, riskshpr_diret, riskshpr_iter], ... [mret, cret, eret, retshpr_fully , retshpr_diret, retshpr_iter], {'Market', 'Cash', 'Equal','Sharpe fully invest', 'Sharpe diret','Sharpe iter'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
当投资组合中没有无风险资产时，换句话说，当投资组合满仓时，有效边界为曲线，对应于上图中的红线。因此，存在一个使夏普比率最大化的唯一（风险, 收益）点，'iterative' 和 'direct' 方法都可以找到该点。如果允许投资组合投资无风险资产，则红色有效边界线的一部分将被资产配置线代替，从而得到具有无风险投资的投资组合的有效边界（蓝线）。直的蓝线上的所有（风险, 收益）点都具有相同的夏普比率。此外，'iterative' 和 'direct' 方法很可能以不同的点结束，因此存在不同的投资组合分配。
在使用 'iterative' 方法时，您可以使用可选的 'TolX' 名称-值参量。TolX 是与有效边界可能的收益水平相关的终止容差。如果选择的 TolX 值与收益范围相比较大，则解的准确性较差。TolX 应该是一个小于 0.01*(maxReturn - minReturn) 的数值。
maxReturn = max(qret); % Max return portfolio minReturn = min(qret); % Min return portfolio display(0.01*(maxReturn-minReturn))
1.5193e-04
增大终止容差的目的是加快 'iterative' 算法的收敛速度。但是，如前所述，解的准确性将降低。您可以在下表中看到这一点。
pwgtshpr_iter_largerTol = estimateMaxSharpeRatio(q, 'Method', 'iterative',... 'TolX', 1e-4); display(table(pwgtshpr_iter, pwgtshpr_iter_largerTol,... 'VariableNames', {'Default TolX = 1e-8','TolX = 1e-4'}))
30×2 table
Default TolX = 1e-8 TolX = 1e-4
___________________ ___________
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0.015523 0.015523
0.052472 0.052473
0 0
0 0
0 0
0.090335 0.090335
0.081562 0.081562
0 0
0.026094 0.026094
0 0
0.043466 0.043466
0 0
0.034997 0.034998
0 0
0.1285 0.1285
0.10979 0.10979
在上表中，权重的值与使用默认容差获得的权重相比略有不同，这符合预期。
为三项资产创建一个 Portfolio 对象。
AssetMean = [ 0.0101110; 0.0043532; 0.0137058 ];
AssetCovar = [ 0.00324625 0.00022983 0.00420395;
0.00022983 0.00049937 0.00019247;
0.00420395 0.00019247 0.00764097 ];
p = Portfolio('AssetMean', AssetMean, 'AssetCovar', AssetCovar);
p = setDefaultConstraints(p); 使用 setBounds 为 i = 1,...NumAssets 的所有资产设置半连续约束，使 xi = 0 或 0.02 <= xi <= 0.5。
p = setBounds(p, 0.02, 0.5,'BoundType', 'Conditional', 'NumAssets', 3);
当使用 Portfolio 对象时，setMinMaxNumAssets 函数支持您为纯多头投资组合设置基数约束。这为 Portfolio 对象设置了基数约束，其中满足非零半连续约束的已分配资产总数介于 MinNumAssets 和 MaxNumAssets 之间。通过设置 MinNumAssets = MaxNumAssets = 2，仅对投资组合的三项资产中的两项进行了投资。
p = setMinMaxNumAssets(p, 2, 2);
使用 estimateMaxSharpeRatio 估计有效投资组合以最大化夏普比率。
weights = estimateMaxSharpeRatio(p,'Method','iterative')
weights = 3×1
0
0.5000
0.5000
estimateMaxSharpeRatio 函数使用 MINLP 求解器来求解此问题。使用 setSolverMINLP 函数来配置 SolverType 和选项。
p.solverOptionsMINLP
ans = struct with fields:
MaxIterations: 1000
AbsoluteGapTolerance: 1.0000e-07
RelativeGapTolerance: 1.0000e-05
NonlinearScalingFactor: 1000
ObjectiveScalingFactor: 1000
Display: 'off'
CutGeneration: 'basic'
MaxIterationsInactiveCut: 30
ActiveCutTolerance: 1.0000e-07
IntMainSolverOptions: [1×1 optim.options.Intlinprog]
NumIterationsEarlyIntegerConvergence: 30
ExtendedFormulation: 0
NumInnerCuts: 10
NumInitialOuterCuts: 10
输入参数
名称-值参数
输出参量
详细信息
提示
您也可以使用圆点表示法来估计最大化夏普比率的有效投资组合。
[pwgt,pbuy,psell] = obj.estimateMaxSharpeRatio;
算法
通过使用 'direct' 或 'iterative' 方法来实现夏普比率最大化。对于 'direct' 方法，假定有以下情形。最大化夏普比率的公式为：
其中，μ 和 C 是均值和协方差矩阵，rf 为无风险利率。
对于所有 x，如果 μT x - rf ≤ 0，则使夏普比率最大化的投资组合就是具有最大收益率的投资组合。
如果 μTx - rf > 0，则使
且 y = tx (Cornuejols [1] section 8.2)。然后，通过一些替换，您可以将原始问题转换为以下形式：
只需求解一次优化，因此称为 “direct”。可以通过以下方式恢复投资组合权重：x* = y* / t*。
对于 'iterative' 方法，目的是通过迭代方式在有效边界上探索不同收益率水平的投资组合，并找到具有最大夏普比率的投资组合。因此，在此过程中会求解多个优化问题，而不像使用 'direct' 方法时只需求解一次。因此，与 'direct' 方法相比，'iterative' 方法要慢一些。
参考
[1] Cornuejols, G. and Reha Tütüncü. Optimization Methods in Finance. Cambridge University Press, 2007.
版本历史记录
在 R2011b 中推出
