estimatePortMoments
估计 Portfolio 对象的投资组合收益矩
说明
示例
给定投资组合 p，使用 estimatePortMoments 函数来显示有效投资组合的风险和收益范围。
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p = setAssetMoments(p, m, C);
p = setDefaultConstraints(p);
pwgt = estimateFrontierLimits(p);
[prsk, pret] = estimatePortMoments(p, pwgt);
disp([prsk, pret]); 0.0769 0.0590
0.3500 0.1800
为三项资产创建一个 Portfolio 对象。
AssetMean = [ 0.0101110; 0.0043532; 0.0137058 ];
AssetCovar = [ 0.00324625 0.00022983 0.00420395;
0.00022983 0.00049937 0.00019247;
0.00420395 0.00019247 0.00764097 ];
p = Portfolio('AssetMean', AssetMean, 'AssetCovar', AssetCovar);
p = setDefaultConstraints(p); 使用 setBounds 为 i=1,...NumAssets 的所有资产设置半连续约束，使 xi=0 或 0.02<=xi<=0.5。
p = setBounds(p, 0.02, 0.5,'BoundType', 'Conditional', 'NumAssets', 3);
当使用 Portfolio 对象时，setMinMaxNumAssets 函数支持您为纯多头投资组合设置基数约束。这为 Portfolio 对象设置了基数约束，其中满足非零半连续约束的已分配资产总数介于 MinNumAssets 和 MaxNumAssets 之间。通过设置 MinNumAssets=MaxNumAssets=2，仅对投资组合的三项资产中的两项进行了投资。
p = setMinMaxNumAssets(p, 2, 2);
使用 estimatePortMoments 估计 Portfolio 对象的投资组合收益矩。
pwgt = estimateFrontierLimits(p); [prsk, pret] = estimatePortMoments(p, pwgt)
prsk = 2×1
0.0324
0.0695
pret = 2×1
0.0072
0.0119
estimatePortMoments 函数使用 MINLP 求解器来求解此问题。使用 setSolverMINLP 函数来配置 SolverType 和选项。
p.solverOptionsMINLP
ans = struct with fields:
MaxIterations: 1000
AbsoluteGapTolerance: 1.0000e-07
RelativeGapTolerance: 1.0000e-05
NonlinearScalingFactor: 1000
ObjectiveScalingFactor: 1000
Display: 'off'
CutGeneration: 'basic'
MaxIterationsInactiveCut: 30
ActiveCutTolerance: 1.0000e-07
IntMainSolverOptions: [1×1 optim.options.Intlinprog]
NumIterationsEarlyIntegerConvergence: 30
ExtendedFormulation: 0
NumInnerCuts: 10
NumInitialOuterCuts: 10
Portfolio 对象能够找到与指定的目标风险相关的有效投资组合。
加载投资组合
加载一个 30 支股票的预期收益向量和协方差矩阵。
load StockStats使用默认约束创建 Portfolio 对象
Portfolio 对象的默认约束是，它是一个纯多头投资组合并且满仓。还可以使用很多其他约束类型。
P = Portfolio('mean',expRet,'covar',expCov); P = setDefaultConstraints(P);
绘制完整有效边界
将 plotFrontier 函数与 Portfolio 对象结合使用以可视化完整边界。还存在其他函数可以让您沿着边界查看特定投资组合。
P.plotFrontier
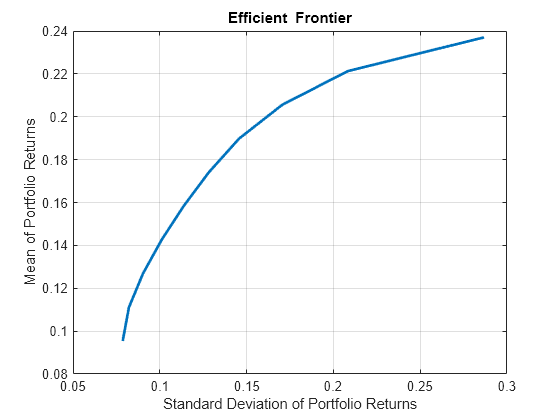
捕获投资组合风险和收益的上界和下界
它有助于了解沿有效边界投资组合矩的上限和下限是什么。通过此信息可确定可行目标有哪些。将 estimateFrontierLimits 函数与 Portfolio 对象结合使用以确定这些极值的权重。然后，您可以对 Portfolio 对象使用 estimatePortMoments 函数来计算极限矩。
P_Weights1 = P.estimateFrontierLimits; [P_risklimits, P_returnlimits] = P.estimatePortMoments(P_Weights1)
P_risklimits = 2×1
0.0786
0.2868
P_returnlimits = 2×1
0.0954
0.2370
使用目标收益估计有效投资组合
在可行域中的某个位置为投资组合选择一个目标收益。您可以使用 estimateFrontierByRisk 估计投资组合中的各投资的比例，然后使用 estimatePortMoments 确定它的矩。
targetReturn = 0.15; P_Weights2 = P.estimateFrontierByReturn(targetReturn); [P_risk2, P_return2] = P.estimatePortMoments(P_Weights2)
P_risk2 = 0.1068
P_return2 = 0.1500
收益与 targetReturn 值匹配，风险与有效边界图一致。
使用目标风险估计有效投资组合
Portfolio 对象能够使用指定目标风险找到有效投资组合。
targetRisk = 0.2; P_Weights3 = P.estimateFrontierByRisk(targetRisk); [P_risk3, P_return3] = P.estimatePortMoments(P_Weights3)
P_risk3 = 0.2000
P_return3 = 0.2182
estimateFrontierByReturn 和 estimateFrontierByRisk 函数的另一个有用的功能是，在您指定了不可行（太高或太低）目标时触发特定事件。在这种情况下，这些函数提供一条警告消息来给出最佳方案。
输入参数
输出参量
详细信息
提示
您还可以使用圆点表示法来估计投资组合收益矩。
[prsk, pret] = obj.estimatePortMoments(pwgt);
版本历史记录
在 R2011a 中推出
