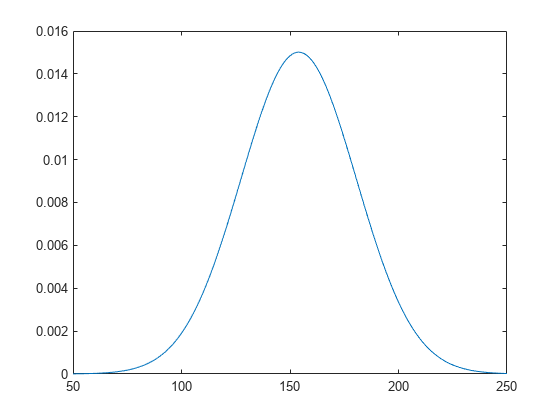
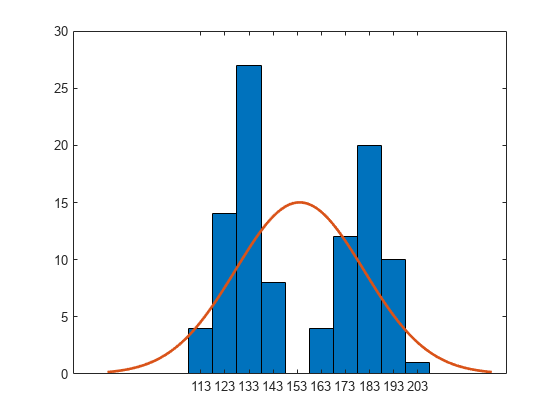
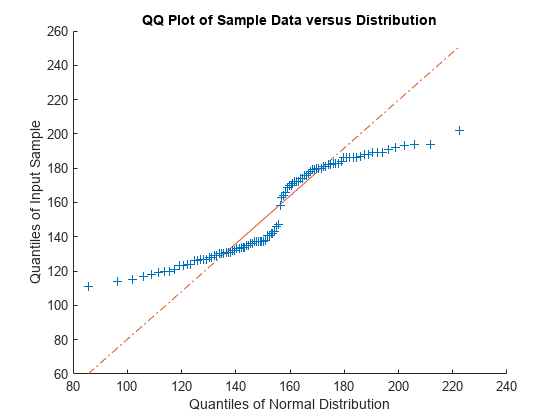
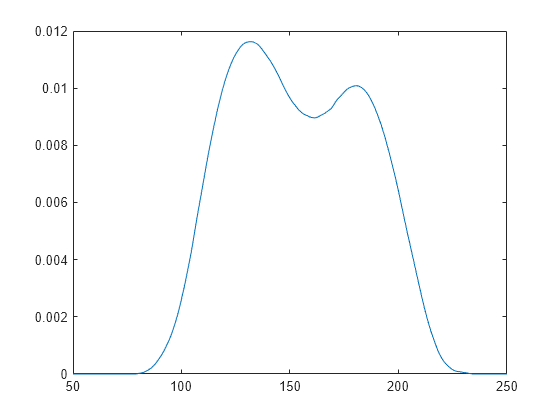
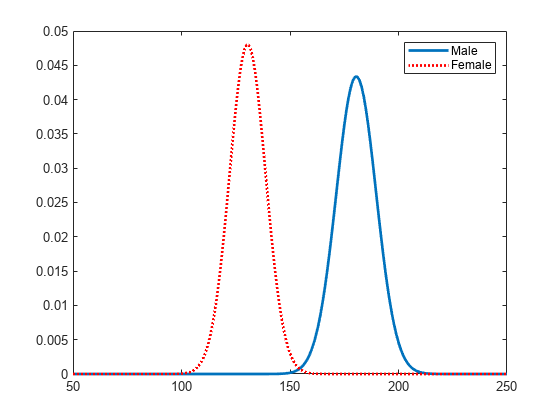
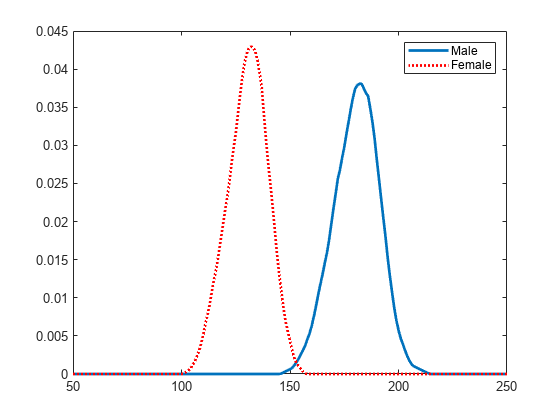
fitdist
对数据进行概率分布对象拟合
语法
说明
pd = fitdist(x,distname,Name,Value)
示例
对样本数据进行正态分布拟合，并使用直方图和分位数-分位数图检查拟合情况。
从数据文件 patients.mat 中加载患者体重。
load patients
x = Weight;通过对数据进行正态分布拟合来创建正态分布对象。
pd = fitdist(x,'Normal')pd =
NormalDistribution
Normal distribution
mu = 154 [148.728, 159.272]
sigma = 26.5714 [23.3299, 30.8674]
分布对象的输出包括均值 (mu) 和标准差 (sigma) 的参数估计值，以及每个参数的 95% 置信区间。
您可以使用 pd 的对象函数来计算分布并生成随机数。显示支持的对象函数。
methods(pd)
Methods for class prob.NormalDistribution: cdf gather icdf iqr mean median negloglik paramci pdf plot proflik random std truncate var
例如，使用 paramci 函数获得 95% 置信区间。
ci95 = paramci(pd)
ci95 = 2×2
148.7277 23.3299
159.2723 30.8674
指定显著性水平 (Alpha) 以获得具有不同置信水平的置信区间。计算 99% 置信区间。
ci99 = paramci(pd,'Alpha',.01)ci99 = 2×2
147.0213 22.4257
160.9787 32.4182
计算并绘制分布的 pdf 值。
x_values = 50:1:250; y = pdf(pd,x_values); plot(x_values,y)
使用 histfit 函数创建具有正态分布拟合的直方图。histfit 使用 fitdist 对数据进行分布拟合。
histfit(x)
直方图显示数据有两种模式，正态分布拟合模式介于这两种模式之间。
使用 qqplot 创建样本数据 x 的分位数对拟合分布的理论分位数值的分位数-分位数图。
qqplot(x,pd)
绘图不是一条直线，说明数据不遵循正态分布。
从数据文件 patients.mat 中加载患者体重。
load patients
x = Weight;通过对数据进行核分布拟合来创建核分布对象。使用依潘涅契科夫核函数。
pd = fitdist(x,'Kernel','Kernel','epanechnikov')
pd =
KernelDistribution
Kernel = epanechnikov
Bandwidth = 14.3792
Support = unbounded
绘制分布的 pdf。
x_values = 50:1:250; y = pdf(pd,x_values); plot(x_values,y)
从数据文件 patients.mat 中加载患者体重和性别。
load patients
x = Weight;通过对按患者性别分组的数据进行正态分布拟合来创建正态分布对象。
[pdca,gn,gl] = fitdist(x,'Normal','By',Gender)
pdca=1×2 cell array
{1×1 prob.NormalDistribution} {1×1 prob.NormalDistribution}
gn = 2×1 cell
{'Male' }
{'Female'}
gl = 2×1 cell
{'Male' }
{'Female'}
元胞数组 pdca 包含两个概率分布对象，分别对应每个性别组。元胞数组 gn 包含两个分组标签。元胞数组 gl 包含两个组水平。
查看元胞数组 pdca 中的各个分布，比较各性别的均值 mu 和标准差 sigma。
female = pdca{1} % Distribution for femalesfemale =
NormalDistribution
Normal distribution
mu = 180.532 [177.833, 183.231]
sigma = 9.19322 [7.63933, 11.5466]
male = pdca{2} % Distribution for malesmale =
NormalDistribution
Normal distribution
mu = 130.472 [128.183, 132.76]
sigma = 8.30339 [6.96947, 10.2736]
计算每个分布的 pdf。
x_values = 50:1:250; femalepdf = pdf(female,x_values); malepdf = pdf(male,x_values);
对 pdf 绘图，以直观地比较各性别的体重分布。
figure plot(x_values,femalepdf,'LineWidth',2) hold on plot(x_values,malepdf,'Color','r','LineStyle',':','LineWidth',2) legend(gn,'Location','NorthEast') hold off
从数据文件 patients.mat 中加载患者体重和性别。
load patients
x = Weight;通过对按患者性别分组的数据进行核分布拟合来创建核分布对象。使用三角核函数。
[pdca,gn,gl] = fitdist(x,'Kernel','By',Gender,'Kernel','triangle');
查看元胞数组 pdca 中的每个分布，以了解每个性别的核分布。
female = pdca{1} % Distribution for femalesfemale =
KernelDistribution
Kernel = triangle
Bandwidth = 5.08961
Support = unbounded
male = pdca{2} % Distribution for malesmale =
KernelDistribution
Kernel = triangle
Bandwidth = 4.25894
Support = unbounded
计算每个分布的 pdf。
x_values = 50:1:250; femalepdf = pdf(female,x_values); malepdf = pdf(male,x_values);
对 pdf 绘图，以直观地比较各性别的体重分布。
figure plot(x_values,femalepdf,'LineWidth',2) hold on plot(x_values,malepdf,'Color','r','LineStyle',':','LineWidth',2) legend(gn,'Location','NorthEast') hold off
输入参数
名称-值参数
输出参量
算法
fitdist 函数使用最大似然估计来拟合大多数分布。两个例外是带有未删失数据的正态分布和对数正态分布。
对于未删失的正态分布，sigma 参数的估计值是方差的无偏估计值的平方根。
对于未删失的对数正态分布，sigma 参数的估计值是数据对数的方差的无偏估计值的平方根。
替代功能
分布拟合器打开一个图形用户界面，以便您从工作区导入数据，并以交互方式对该数据进行概率分布拟合。然后，您可以将分布作为概率分布对象保存到工作区。在命令行中使用
distributionFitter打开分布拟合器，或点击 App 选项卡上的“分布拟合器”。要对左删失、双删失或区间删失数据进行分布拟合，请使用
mle。您可以使用mle函数找到最大似然估计值，并使用makedist函数创建一个概率分布对象。有关示例，请参阅Find MLEs for Double-Censored Data。
参考
[1] Johnson, N. L., S. Kotz, and N. Balakrishnan. Continuous Univariate Distributions. Vol. 1, Hoboken, NJ: Wiley-Interscience, 1993.
[2] Johnson, N. L., S. Kotz, and N. Balakrishnan. Continuous Univariate Distributions. Vol. 2, Hoboken, NJ: Wiley-Interscience, 1994.
[3] Bowman, A. W., and A. Azzalini. Applied Smoothing Techniques for Data Analysis. New York: Oxford University Press, 1997.
