cdf

累积分布函数

全页折叠

语法

y = cdf(name,x,A)

y = cdf(name,x,A,B)

y = cdf(name,x,A,B,C)

y = cdf(name,x,A,B,C,D)

y = cdf(pd,x)

y = cdf(___,'upper')

说明

y = cdf(name,x,A) 基于 x 中的值计算并返回由 name 和分布参数 A 指定的单参数分布族的累积分布函数 (cdf) 值。

y = cdf(name,x,A,B) 基于 x 中的值计算并返回由 name 以及分布参数 A 和 B 指定的双参数分布族的 cdf。

示例

y = cdf(name,x,A,B,C) 基于 x 中的值计算并返回由 name 以及分布参数 A、B 和 C 指定的三参数分布族的 cdf。

y = cdf(name,x,A,B,C,D) 基于 x 中的值计算并返回由 name 以及分布参数 A、B、C 和 D 指定的四参数分布族的 cdf。

y = cdf(pd,x) 基于 x 中的值计算并返回概率分布对象 pd 的 cdf。

示例

y = cdf(___,'upper') 使用可更精确计算极端上尾概率的算法返回 cdf 的补函数。'upper' 可以跟在上述语法中的任何输入参量之后。

示例

全部折叠

通过指定分布名称和参数计算正态分布 cdf

打开实时脚本

通过指定分布名称 'Normal' 和分布参数，计算正态分布的 cdf 值。

定义输入向量 x 以包含用于计算 cdf 的值。

x = [-2,-1,0,1,2];

计算均值 $μ$ 等于 1、标准差 $σ$ 等于 5 的正态分布的 cdf 值。

mu = 1;
sigma = 5;
y = cdf('Normal',x,mu,sigma)

y = 1×5

    0.2743    0.3446    0.4207    0.5000    0.5793

y 中的每个值对应于输入向量 x 中的一个值。例如，在值 x 等于 1 时，对应的 cdf 值 y 等于 0.5000。

使用分布对象计算正态分布 cdf

打开实时脚本

创建一个正态分布对象，并使用该对象计算正态分布的 cdf 值。

创建均值 $μ$ 等于 1、标准差 $σ$ 等于 5 的正态分布对象。

mu = 1;
sigma = 5;
pd = makedist('Normal','mu',mu,'sigma',sigma);

定义输入向量 x 以包含用于计算 cdf 的值。

x = [-2,-1,0,1,2];

基于 x 中的值计算正态分布的 cdf 值。

y = cdf(pd,x)

y = 1×5

    0.2743    0.3446    0.4207    0.5000    0.5793

y 中的每个值对应于输入向量 x 中的一个值。例如，在值 x 等于 1 时，对应的 cdf 值 y 等于 0.5000。

计算泊松分布 cdf

打开实时脚本

创建一个泊松分布对象，使用的速率参数 $λ$ 等于 2。

lambda = 2;
pd = makedist('Poisson','lambda',lambda);

定义输入向量 x 以包含用于计算 cdf 的值。

x = [0,1,2,3,4];

基于 x 中的值计算泊松分布的 cdf 值。

y = cdf(pd,x)

y = 1×5

    0.1353    0.4060    0.6767    0.8571    0.9473

y 中的每个值对应于输入向量 x 中的一个值。例如，在值 x 等于 3 时，对应的 cdf 值 y 等于 0.8571。

您也可以不创建概率分布对象而直接计算同样的 cdf 值。使用 cdf 函数，并使用相同的速率参数值指定泊松分布， $λ$ 。

y2 = cdf('Poisson',x,lambda)

y2 = 1×5

    0.1353    0.4060    0.6767    0.8571    0.9473

cdf 值与使用概率分布对象计算的值相同。

绘制标准正态分布 cdf

打开实时脚本

创建一个标准正态分布对象。

pd = makedist('Normal')

pd = 
  NormalDistribution

  Normal distribution
       mu = 0
    sigma = 1

指定 x 值并计算 cdf。

x = -3:.1:3;
p = cdf(pd,x);

绘制标准正态分布的 cdf。

plot(x,p)

Figure contains an axes object. The axes object contains an object of type line.

绘制 gamma 分布 cdf

打开实时脚本

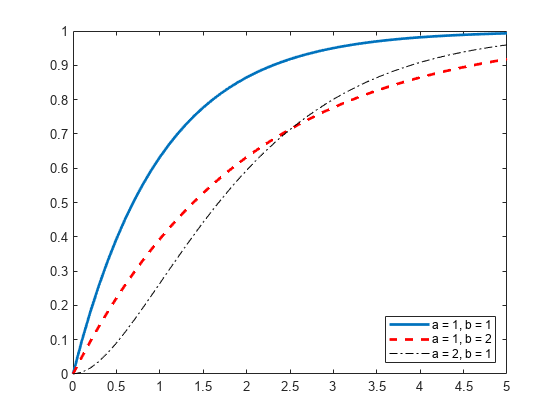
创建三个 gamma 分布对象。第一个使用默认参数值。第二个指定 a = 1 和 b = 2。第三个指定 a = 2 和 b = 1。

pd_gamma = makedist('Gamma')

pd_gamma = 
  GammaDistribution

  Gamma distribution
    a = 1
    b = 1

pd_12 = makedist('Gamma','a',1,'b',2)

pd_12 = 
  GammaDistribution

  Gamma distribution
    a = 1
    b = 2

pd_21 = makedist('Gamma','a',2,'b',1)

pd_21 = 
  GammaDistribution

  Gamma distribution
    a = 2
    b = 1

指定 x 值，并计算每个分布的 cdf。

x = 0:.1:5;
cdf_gamma = cdf(pd_gamma,x);
cdf_12 = cdf(pd_12,x);
cdf_21 = cdf(pd_21,x);

创建一个绘图，该绘图用于可视化在为形状参数 a 和 b 指定不同值时 gamma 分布的 cdf 如何变化。

figure;
J = plot(x,cdf_gamma);
hold on;
K = plot(x,cdf_12,'r--');
L = plot(x,cdf_21,'k-.');
set(J,'LineWidth',2);
set(K,'LineWidth',2);
legend([J K L],'a = 1, b = 1','a = 1, b = 2','a = 2, b = 1','Location','southeast');
hold off;

Figure contains an axes object. The axes object contains 3 objects of type line. These objects represent a = 1, b = 1, a = 1, b = 2, a = 2, b = 1.

对 t 分布进行帕累托尾拟合，并计算 cdf

打开实时脚本

对累积概率为 0.1 和 0.9 的 $t$ 分布进行帕累托尾拟合。

t = trnd(3,100,1);
obj = paretotails(t,0.1,0.9);
[p,q] = boundary(obj)

基于 q 中的值计算 cdf。

cdf(obj,q)

ans = 2×1

    0.1000
    0.9000

输入参数

全部折叠

`name` — 概率分布名称
概率分布名称的字符向量或字符串标量

概率分布名称，指定为下表中的概率分布名称之一。

`name`	分布	输入参数 `A`	输入参数 `B`	输入参数 `C`	输入参数 `D`
`'Beta'`	Beta Distribution	a 第一个形状参数	b 第二个形状参数	不适用	不适用
`'Binomial'`	Binomial Distribution	n 试验次数	p 每次试验成功的概率	不适用	不适用
`'BirnbaumSaunders'`	Birnbaum-Saunders Distribution	β 尺度参数	γ 形状参数	不适用	不适用
`'Burr'`	Burr Type XII Distribution	α 尺度参数	c 第一个形状参数	k 第二个形状参数	不适用
`'Chisquare'` 或 `'chi2'`	Chi-Square Distribution	ν 自由度	不适用	不适用	不适用
`'Exponential'`	Exponential Distribution	μ 均值	不适用	不适用	不适用
`'Extreme Value'` 或 `'ev'`	Extreme Value Distribution	μ 位置参量	σ 尺度参数	不适用	不适用
`'F'`	F Distribution	ν₁ 分子自由度	ν₂ 分母自由度	不适用	不适用
`'Gamma'`	Gamma Distribution	a 形状参数	b 尺度参数	不适用	不适用
`'Generalized Extreme Value'` 或 `'gev'`	Generalized Extreme Value Distribution	k 形状参数	σ 尺度参数	μ 位置参量	不适用
`'Generalized Pareto'` 或 `'gp'`	Generalized Pareto Distribution	k 尾部指数（形状）参数	σ 尺度参数	μ 阈值（位置）参数	不适用
`'Geometric'`	Geometric Distribution	p 概率参数	不适用	不适用	不适用
`'Half Normal'` 或 `'hn'`	Half-Normal Distribution	μ 位置参量	σ 尺度参数	不适用	不适用
`'Hypergeometric'` 或 `'hyge'`	Hypergeometric Distribution	m 总体的大小	k 总体中具有所需特征的项数	n 抽取的样本数量	不适用
`'InverseGaussian'`	逆高斯分布	μ 尺度参数	λ 形状参数	不适用	不适用
`'Logistic'`	逻辑分布	μ 均值	σ 尺度参数	不适用	不适用
`'LogLogistic'`	Loglogistic Distribution	μ 对数值的均值	σ 对数值的尺度参数	不适用	不适用
`'LogNormal'`	对数正态分布	μ 对数值的均值	σ 对数值的标准差	不适用	不适用
`'Loguniform'`	Loguniform Distribution	a 下部端点（最小值）	b 上部端点（最大值）	不适用	不适用
`'Pearson'`	Pearson Distribution	μ 均值	σ 标准差	γ 偏度	κ 峰度
`'Nakagami'`	Nakagami 分布	μ 形状参数	ω 尺度参数	不适用	不适用
`'Negative Binomial'` 或 `'nbin'`	Negative Binomial Distribution	r 成功次数	p 单个试验的成功概率	不适用	不适用
`'Noncentral F'` 或 `'ncf'`	Noncentral F Distribution	ν₁ 分子自由度	ν₂ 分母自由度	δ 非中心参数	不适用
`'Noncentral t'` 或 `'nct'`	Noncentral t Distribution	ν 自由度	δ 非中心参数	不适用	不适用
`'Noncentral Chi-square'` 或 `'ncx2'`	Noncentral Chi-Square Distribution	ν 自由度	δ 非中心参数	不适用	不适用
`'Normal'`	正态分布	μ 均值	σ 标准差	不适用	不适用
`'Poisson'`	泊松分布	λ 均值	不适用	不适用	不适用
`'Rayleigh'`	瑞利分布	b 尺度参数	不适用	不适用	不适用
`'Rician'`	Rician Distribution	s 非中心参数	σ 尺度参数	不适用	不适用
`'Stable'`	Stable Distribution	α 第一个形状参数	β 第二个形状参数	γ 尺度参数	δ 位置参量
`'T'`	Student's t Distribution	ν 自由度	不适用	不适用	不适用
`'tLocationScale'`	t Location-Scale Distribution	μ 位置参量	σ 尺度参数	ν 形状参数	不适用
`'Uniform'`	Uniform Distribution (Continuous)	a 下部端点（最小值）	b 上部端点（最大值）	不适用	不适用
`'Discrete Uniform'` 或 `'unid'`	Uniform Distribution (Discrete)	n 最大可观测值	不适用	不适用	不适用
`'Weibull'` 或 `'wbl'`	Weibull Distribution	a 尺度参数	b 形状参数	不适用	不适用

示例: 'Normal'

`x` — 用于计算 cdf 的值
标量值 | 标量值组成的数组

用于计算 cdf 的值，指定为标量值或标量值组成的数组。

如果输入参量 x、A、B、C 和 D 中的一个或多个是数组，则数组大小必须相同。在这种情况下，cdf 将每个标量输入扩展为与数组输入大小相同的常量数组。请参阅 name 了解每个分布的 A、B、C 和 D 的定义。

示例: [0.1,0.25,0.5,0.75,0.9]

数据类型: single | double

`A` — 第一概率分布参数
标量值 | 标量值组成的数组

第一概率分布参数，指定为标量值或标量值组成的数组。

数据类型: single | double

`B` — 第二概率分布参数
标量值 | 标量值组成的数组

第二概率分布参数，指定为标量值或标量值组成的数组。

数据类型: single | double

`C` — 第三概率分布参数
标量值 | 标量值组成的数组

第三概率分布参数，指定为标量值或标量值组成的数组。

数据类型: single | double

`D` — 第四概率分布参数
标量值 | 标量值组成的数组

第四概率分布参数，指定为标量值或标量值组成的数组。

数据类型: single | double

`pd` — 概率分布
概率分布对象

概率分布，指定为下表中的概率分布对象之一。

分布对象	用于创建概率分布对象的函数或 App
`BetaDistribution`	`makedist`、`fitdist`、分布拟合器
`BinomialDistribution`	`makedist`、`fitdist`、分布拟合器
`BirnbaumSaundersDistribution`	`makedist`、`fitdist`、分布拟合器
`BurrDistribution`	`makedist`、`fitdist`、分布拟合器
`ExponentialDistribution`	`makedist`、`fitdist`、分布拟合器
`ExtremeValueDistribution`	`makedist`、`fitdist`、分布拟合器
`GammaDistribution`	`makedist`、`fitdist`、分布拟合器
`GeneralizedExtremeValueDistribution`	`makedist`、`fitdist`、分布拟合器
`GeneralizedParetoDistribution`	`makedist`、`fitdist`、分布拟合器
`HalfNormalDistribution`	`makedist`、`fitdist`、分布拟合器
`InverseGaussianDistribution`	`makedist`、`fitdist`、分布拟合器
`KernelDistribution`	`fitdist`、分布拟合器
`LogisticDistribution`	`makedist`、`fitdist`、分布拟合器
`LoglogisticDistribution`	`makedist`、`fitdist`、分布拟合器
`LognormalDistribution`	`makedist`、`fitdist`、分布拟合器
`LoguniformDistribution`	`makedist`
`MultinomialDistribution`	`makedist`
`NakagamiDistribution`	`makedist`、`fitdist`、分布拟合器
`NegativeBinomialDistribution`	`makedist`、`fitdist`、分布拟合器
`NormalDistribution`	`makedist`、`fitdist`、分布拟合器
尾部具有广义帕累托分布的分段分布	`paretotails`
`PiecewiseLinearDistribution`	`makedist`
`PoissonDistribution`	`makedist`、`fitdist`、分布拟合器
`RayleighDistribution`	`makedist`、`fitdist`、分布拟合器
`RicianDistribution`	`makedist`、`fitdist`、分布拟合器
`StableDistribution`	`makedist`、`fitdist`、分布拟合器
`tLocationScaleDistribution`	`makedist`、`fitdist`、分布拟合器
`TriangularDistribution`	`makedist`
`UniformDistribution`	`makedist`
`WeibullDistribution`	`makedist`、`fitdist`、分布拟合器

输出参量

全部折叠

`y` — cdf 值
标量值 | 标量值组成的数组

cdf 值，以标量值或标量值组成的数组形式返回。在经过任何必要的标量扩展后，y 的大小与 x 相同。y 中的每个元素均为由分布参数（A、B、C 和 D）中的对应元素或概率分布对象 (pd) 指定的分布的 cdf 值，其值在 x 中的对应元素处进行计算。

替代功能

cdf 是泛型函数，它按名称 name 或概率分布对象 pd 接受分布。使用分布特有的函数更快，例如正态分布特有的 normcdf，二项分布特有的 binocdf。有关特定于分布的函数的列表，请参阅Supported Distributions。
使用 Probability Distribution Function 为概率分布创建累积分布函数 (cdf) 或概率密度函数 (pdf) 的交互图。

扩展功能

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

输入参量 name 必须为编译时常量。例如，要使用正态分布，请将 coder.Constant('Normal') 包含在 codegen (MATLAB Coder) 的 -args 值中。
输入参量 pd 可以是 beta、指数、极值、对数正态、正态和威布尔分布的拟合概率分布对象。通过对来自 fitdist 函数的样本数据进行概率分布拟合，创建 pd。有关示例，请参阅Code Generation for Probability Distribution Objects。

有关代码生成的详细信息，请参阅 Introduction to Code Generation 和 General Code Generation Workflow。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

此函数完全支持 GPU 数组。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

全部展开

R2023b: 支持皮尔逊分布

从 R2023b 开始，cdf 支持皮尔逊分布。

另请参阅

cdf

语法

说明

示例

通过指定分布名称和参数计算正态分布 cdf

使用分布对象计算正态分布 cdf

计算泊松分布 cdf

绘制标准正态分布 cdf

绘制 gamma 分布 cdf

对 t 分布进行帕累托尾拟合，并计算 cdf

输入参数

name — 概率分布名称 概率分布名称的字符向量或字符串标量

x — 用于计算 cdf 的值 标量值 | 标量值组成的数组

A — 第一概率分布参数 标量值 | 标量值组成的数组

B — 第二概率分布参数 标量值 | 标量值组成的数组

C — 第三概率分布参数 标量值 | 标量值组成的数组

D — 第四概率分布参数 标量值 | 标量值组成的数组

pd — 概率分布 概率分布对象

输出参量

y — cdf 值 标量值 | 标量值组成的数组

替代功能

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

版本历史记录

R2023b: 支持皮尔逊分布

另请参阅

主题

WeChat

`name` — 概率分布名称
概率分布名称的字符向量或字符串标量

`x` — 用于计算 cdf 的值
标量值 | 标量值组成的数组

`A` — 第一概率分布参数
标量值 | 标量值组成的数组

`B` — 第二概率分布参数
标量值 | 标量值组成的数组

`C` — 第三概率分布参数
标量值 | 标量值组成的数组

`D` — 第四概率分布参数
标量值 | 标量值组成的数组

`pd` — 概率分布
概率分布对象

`y` — cdf 值
标量值 | 标量值组成的数组

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。