正态分布
概述
正态分布,有时称为高斯分布,是双参数曲线族。使用正态分布建模的通常理由是中心极限定理,该定理(粗略地)指出,随着样本大小趋向无穷,来自任何具有有限均值和方差的分布的独立样本总和会收敛为正态分布。
Statistics and Machine Learning Toolbox™ 提供了几种处理正态分布的方法。
参数
正态分布使用下列参数。
| 参数 | 描述 | 支持 |
|---|---|---|
mu (μ) | 均值 | |
sigma (σ) | 标准差 |
标准正态分布具有零均值和单位标准差。如果 z 是标准正态,则 σz + µ 也是正态,其均值为 µ,标准差为 σ。相反,如果 x 是均值为 µ、标准差为 σ 的正态,则 z = (x – µ) / σ 为标准正态。
参数估计
最大似然估计 (MLE) 是最大化似然函数的参数估计。正态分布的 μ 和 σ2 的最大似然估计量分别是
和
是样本 x1, x2, …, xn 的样本均值。样本均值是参数 μ 的无偏估计量。但是,s2MLE 是参数 σ2 的有偏估计量,这意味着其预期值不等于参数。
最小方差无偏估计量 (MVUE) 通常用于估计正态分布的参数。MVUE 是参数的所有无偏估计量中方差最小的估计量。正态分布的参数 μ 和 σ2 的 MVUE 分别是样本均值 x̄ 和样本方差 s2。
要对数据进行正态分布拟合并求出参数估计值,请使用 normfit、fitdist 或 mle。
对于未删失数据,
normfit和fitdist计算无偏估计值,mle计算最大似然估计值。对于删失数据,
normfit、fitdist、mle计算最大似然估计值。
与返回参数估计值的 normfit 和 mle 不同,fitdist 返回拟合的概率分布对象 NormalDistribution。对象属性 mu 和 sigma 存储参数估计值。
有关示例,请参阅拟合正态分布对象。
概率密度函数
正态概率密度函数 (pdf) 是
似然函数是被视为参数函数的 pdf。最大似然估计 (MLE) 是 x 取固定值时最大化似然函数的参数估计。
有关示例,请参阅计算并绘制正态分布 pdf。
累积分布函数
正态累积分布函数 (cdf) 表示为
p 是参数为 μ 和 σ 的正态分布中的一个观测值落入 (-∞,x] 区间的概率。
标准正态累积分布函数 Φ(x) 在功能上与误差函数 erf 相关。
其中
有关示例,请参阅绘制标准正态分布 cdf。
示例
拟合正态分布对象
加载样本数据并创建包含学生考试成绩数据的第一列的向量。
load examgrades
x = grades(:,1);通过对数据进行正态分布拟合来创建正态分布对象。
pd = fitdist(x,'Normal')pd =
NormalDistribution
Normal distribution
mu = 75.0083 [73.4321, 76.5846]
sigma = 8.7202 [7.7391, 9.98843]
参数估计值旁边的区间是分布参数的 95% 置信区间。
估计参数
使用 normfit 函数估计正态分布参数(均值和标准差)。
加载样本数据并创建包含学生考试成绩数据的第一列的向量。
load examgrades
x = grades(:,1);求参数估计值和 95% 置信区间。
[mu,s,muci,sci] = normfit(x)
mu = 75.0083
s = 8.7202
muci = 2×1
73.4321
76.5846
sci = 2×1
7.7391
9.9884
normfit 函数返回 的最小方差无偏估计量 (MVUE)、 的 MVUE 的平方根以及 和 的 95% 置信区间。
请注意,s 的平方是方差的 MVUE。
s^2
ans = 76.0419
计算并绘制正态分布 pdf
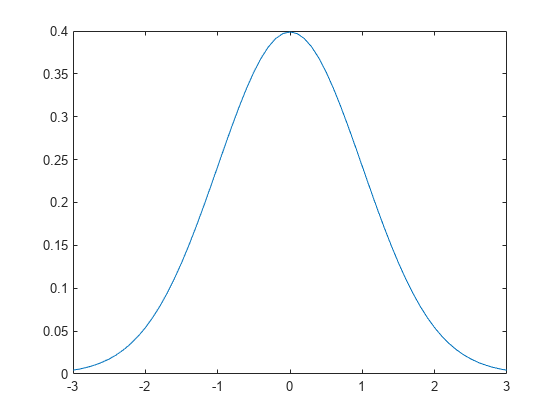
计算参数 等于 0、 等于 1 的标准正态分布的 pdf。
x = [-3:.1:3]; y = normpdf(x,0,1);
绘制 pdf。
plot(x,y)
绘制标准正态分布 cdf
创建一个标准正态分布对象。
pd = makedist('Normal')pd =
NormalDistribution
Normal distribution
mu = 0
sigma = 1
指定 x 值并计算 cdf。
x = -3:.1:3; p = cdf(pd,x);
绘制标准正态分布的 cdf。
plot(x,p)

比较 gamma 和正态分布 pdf
gamma 分布具有形状参数 和尺度参数 。如果 的值较大,gamma 分布非常接近均值 、方差 的正态分布。
计算参数 a = 100 和 b = 5 的 gamma 分布的 pdf。
a = 100; b = 5; x = 250:750; y_gam = gampdf(x,a,b);
为了进行比较,计算基于 gamma 分布逼近的正态分布的均值、标准差和 pdf。
mu = a*b
mu = 500
sigma = sqrt(a*b^2)
sigma = 50
y_norm = normpdf(x,mu,sigma);
将 gamma 分布和正态分布的 pdf 绘制在同一图窗上。
plot(x,y_gam,'-',x,y_norm,'-.') title('Gamma and Normal pdfs') xlabel('Observation') ylabel('Probability Density') legend('Gamma Distribution','Normal Distribution')
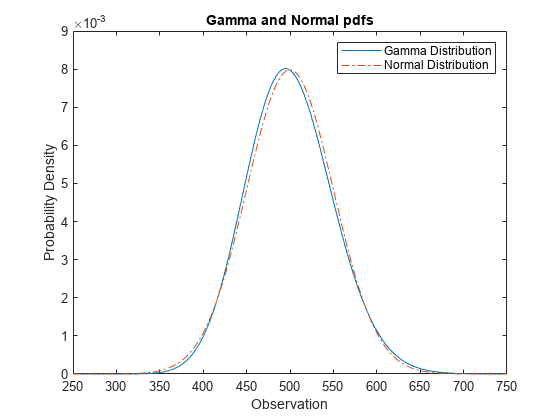
正态分布的 pdf 逼近 gamma 分布的 pdf。
正态分布和对数正态分布之间的关系
如果 X 遵循具有参数 µ 和 σ 的对数正态分布,则 log(X) 遵循具有均值 µ 和标准差 σ 的正态分布。使用分布对象检查正态分布和对数正态分布之间的关系。
通过指定参数值创建对数正态分布对象。
pd = makedist('Lognormal','mu',5,'sigma',2)
pd =
LognormalDistribution
Lognormal distribution
mu = 5
sigma = 2
计算对数正态分布的均值。
mean(pd)
ans = 1.0966e+03
对数正态分布的均值不等于 mu 参数。对数值的均值等于 mu。通过生成随机数来确认这种关系。
从对数正态分布中生成随机数,并计算其对数值。
rng('default'); % For reproducibility x = random(pd,10000,1); logx = log(x);
计算对数值的均值。
m = mean(logx)
m = 5.0033
x 的对数的均值接近 x 的 mu 参数,因为 x 具有对数正态分布。
用正态分布拟合构造 logx 的直方图。
histfit(logx)

该图显示 x 的对数值呈正态分布。
histfit 使用 fitdist 对数据进行分布拟合。使用 fitdist 获得在拟合中使用的参数。
pd_normal = fitdist(logx,'Normal')pd_normal =
NormalDistribution
Normal distribution
mu = 5.00332 [4.96445, 5.04219]
sigma = 1.98296 [1.95585, 2.01083]
估计的正态分布参数接近对数正态分布参数 5 和 2。
比较 Student t 和正态分布 pdf
Student t 分布是依赖于单参数 ν(自由度)的曲线族。随着自由度 ν 趋向无穷,t 分布逼近标准正态分布。
计算参数 nu = 5 的 Student t 分布和参数 nu = 15 的 Student t 分布的 pdf。
x = [-5:0.1:5]; y1 = tpdf(x,5); y2 = tpdf(x,15);
计算标准正态分布的 pdf。
z = normpdf(x,0,1);
将 Student t pdf 和标准正态 pdf 绘制在同一图窗上。
plot(x,y1,'-.',x,y2,'--',x,z,'-') legend('Student''s t Distribution with \nu=5', ... 'Student''s t Distribution with \nu=15', ... 'Standard Normal Distribution','Location','best') xlabel('Observation') ylabel('Probability Density') title('Student''s t and Standard Normal pdfs')

标准正态 pdf 的尾部比 Student t pdf 短。
相关分布
Binomial Distribution - 二项分布对 n 次重复尝试的成功总数和成功概率 p 进行建模。随着 n 的增长,二项分布可以用 µ = np 和 σ2 = np(1–p) 的正态分布来逼近。请参阅Compare Binomial and Normal Distribution pdfs。
Birnbaum-Saunders Distribution - 如果 x 具有参数为 β 和 γ 的伯恩鲍姆-桑德斯分布,则
具有标准正态分布。
卡方分布 - 卡方分布是平方和、独立、标准正态随机变量的分布。如果一组(包含 n 个)观测值呈正态分布,方差为 σ2、样本方差为 s2,则 (n–1)s2/σ2 具有自由度为 n–1 的卡方分布。
normfit函数使用此关系来计算正态参数 σ2 的估计的置信区间。Extreme Value Distribution - 极值分布适用于对尾部呈指数急剧衰减的分布(如正态分布)中的最小值或最大值建模。
Gamma Distribution - gamma 分布具有形状参数 a 和尺度参数 b。如果 a 的值较大,gamma 分布非常接近均值 μ = ab、方差 σ2 = ab2 的正态分布。gamma 分布仅对正实数才有密度。请参阅比较 gamma 和正态分布 pdf。
Half-Normal Distribution - 半正态分布是折叠正态分布和截断正态分布的特例。如果随机变量
Z具有标准正态分布,则 为具有参数 μ 和 σ 的半正态分布。逻辑分布 - 逻辑分布用于增长模型和逻辑回归。与正态分布相比,逻辑分布的尾部更长、峰度更高。
对数正态分布 - 如果 X 遵循具有参数 µ 和 σ 的对数正态分布,则 log(X) 遵循具有均值 µ 和标准差 σ 的正态分布。请参阅正态分布和对数正态分布之间的关系。
多元正态分布 - 多元正态分布是一元正态分布的双变量或多变量泛化。它是相关变量的随机向量的分布,其中每个元素都呈一元正态分布。在最简单的情形下,各变量之间没有相关性,向量的元素是独立的一元正态随机变量。
泊松分布 - 泊松分布是接受非负整数值的单参数离散分布。参数 λ 既是分布的均值,也是分布的方差。随着 λ 的增大,泊松分布可以用 µ = λ 和 σ2 = λ 的正态分布来逼近。
瑞利分布 - 瑞利分布是威布尔分布的特例,应用于通信理论中。如果粒子在 x 和 y 方向上的分量速度是两个独立的正态随机变量(均值为零并具有方差齐性),则粒子在每单位时间行进的距离遵循瑞利分布。
Stable Distribution - 正态分布是稳定分布的特例。第一个形状参数 α = 2 的稳定分布对应于正态分布。
Student's t Distribution - Student t 分布是一个依赖单参数 ν(自由度)的曲线族。随着自由度 ν 趋向无穷,t 分布逼近标准正态分布。请参阅比较 Student t 和正态分布 pdf。
如果 x 是大小为 n 的随机样本,来自均值为 μ 的正态分布,则统计量
(其中 是样本均值,s 是样本标准差)具有包含 n–1 个自由度的 Student t 分布。
t Location-Scale Distribution - t 位置尺度分布适用于对尾部比正态分布重(更容易出现离群值)的数据分布进行建模。当形状参数 ν 趋向无穷时,它逼近正态分布。
参考
[1] Abramowitz, M., and I. A. Stegun. Handbook of Mathematical Functions. New York: Dover, 1964.
[2] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed. Hoboken, NJ: John Wiley & Sons, Inc., 1993.
[3] Lawless, J. F. Statistical Models and Methods for Lifetime Data. Hoboken, NJ: Wiley-Interscience, 1982.
[4] Marsaglia, G., and W. W. Tsang. “A Fast, Easily Implemented Method for Sampling from Decreasing or Symmetric Unimodal Density Functions.” SIAM Journal on Scientific and Statistical Computing. Vol. 5, Number 2, 1984, pp. 349–359.
[5] Meeker, W. Q., and L. A. Escobar. Statistical Methods for Reliability Data. Hoboken, NJ: John Wiley & Sons, Inc., 1998.
另请参阅
NormalDistribution | normcdf | normpdf | norminv | normlike | normstat | normfit | normrnd | erf