卡方分布

概述

卡方 (χ2) 分布是一个单参数曲线族。卡方分布通常用于假设检验，特别是拟合优度卡方检验。

Statistics and Machine Learning Toolbox™ 提供了多种处理卡方分布的方法。

  • 使用分布特定的函数（chi2cdf、chi2inv、chi2pdf、chi2rnd、chi2stat）并指定分布参数。分布特定的函数可以接受多种卡方分布的参数。

  • 将一般分布函数（cdf、icdf、pdf、random）与指定的分布名称 ('Chisquare') 和参数结合使用。

参数

卡方分布使用以下参数。

参数描述支持
nu (ν)自由度ν = 1, 2, 3,...

自由度参数通常是整数，但卡方函数接受任何正值。

两个自由度为 ν1 和 ν2 的卡方随机变量之和是一个自由度为 ν = ν1 + ν2 的卡方随机变量。

概率密度函数

卡方分布的概率密度函数 (pdf) 为

y=f(x|ν)=x(ν−2)/2e−x/22ν2Γ(ν/2),

其中 ν 是自由度，Γ( · ) 是 gamma 函数。

有关示例，请参阅计算卡方分布 pdf。

累积分布函数

卡方分布的累积分布函数 (cdf) 为

p=F(x|ν)=∫0xt(ν−2)/2e−t/22ν/2Γ(ν/2)dt,

其中 ν 是自由度，Γ( · ) 是 Gamma 函数。结果 p 是来自自由度为 ν 的卡方分布的单个观测值落在区间 [0, x] 内的概率。

有关示例，请参阅计算卡方分布 cdf。

逆累积分布函数

卡方分布的逆累积分布函数 (icdf) 为

x=F−1(p|ν)={x:F(x|ν)=p},

其中

p=F(x|ν)=∫0xt(ν−2)/2e−t/22ν/2Γ(ν/2)dt,

ν 是自由度，Γ( · ) 是 gamma 函数。结果 p 是来自自由度为 ν 的卡方分布的单个观测值落在区间 [0, x] 内的概率。

描述性统计量

卡方分布的均值为 ν。

卡方分布的方差为 2ν。

示例

计算卡方分布 pdf

打开实时脚本

计算具有 4 个自由度的卡方分布的 pdf。

x = 0:0.2:15;
y = chi2pdf(x,4);

绘制 pdf。

figure;
plot(x,y)
xlabel('Observation')
ylabel('Probability Density')

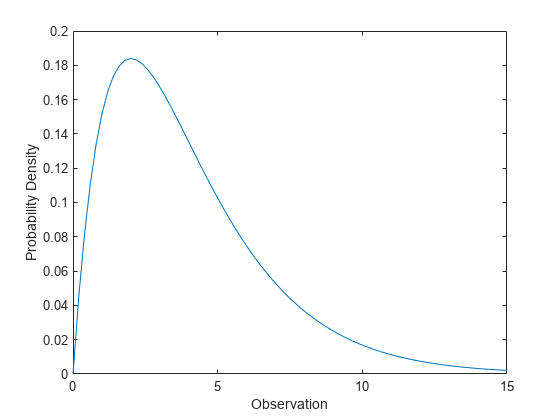
Figure contains an axes object. The axes object with xlabel Observation, ylabel Probability Density contains an object of type line.

卡方分布向右偏斜，尤其是在自由度数量较少时。

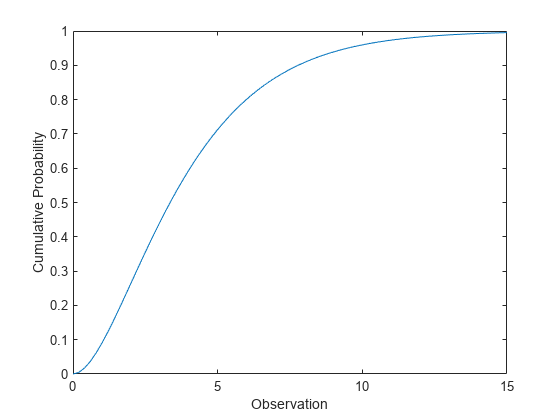
计算卡方分布 cdf

打开实时脚本

计算具有 4 个自由度的卡方分布的 cdf。

x = 0:0.2:15;
y = chi2cdf(x,4);

绘制 cdf。

figure;
plot(x,y)
xlabel('Observation')
ylabel('Cumulative Probability')

Figure contains an axes object. The axes object with xlabel Observation, ylabel Cumulative Probability contains an object of type line.

相关分布

  • F Distribution - F 分布是具有参数 ν1（分子自由度）和 ν2（分母自由度）的双参数化分布。F 分布可以定义为比率 F=χ12ν1χ22ν2，其中 χ21 和 χ22 都是独立的且分别服从具有 ν1 和 ν2 个自由度的卡方分布。

  • Gamma Distribution - gamma 分布是具有参数 a（形状）和 b（尺度）的双参数连续分布。卡方分布等于 2a = ν 和 b = 2 的 gamma 分布。

  • Noncentral Chi-Square Distribution - 非中心卡方分布是具有参数 ν（自由度）和 δ（非中心）的双参数连续分布。当 δ = 0 时，非中心卡方分布等于卡方分布。

  • 正态分布 - 正态分布是双参数连续分布，具有参数 μ（均值）和 σ（标准差）。当 μ = 0、σ = 1 时，便会出现标准正态分布。

    如果 Z1, Z2, …, Zn 是独立的标准正态随机变量，则 ∑i=1nZi2 具有自由度为 ν = n – 1 的卡方分布。

    如果一组（包含 n 个）观测值呈正态分布，方差为 σ2，样本方差为 s2，则 (n−1)s2σ2 具有自由度为 ν = n – 1 的卡方分布。此关系用于在函数 normfit 中计算正态参数 σ2 的估计的置信区间。

  • Student's t Distribution - Student t 分布是具有参数 ν（自由度）的单参数连续分布。如果 Z 具有标准正态分布，χ2 具有自由度为 ν 的卡方分布，并且 Z 和 χ2 是独立的，则 t = Zχ2/ν 具有自由度为 ν 的 Student t 分布。

  • Wishart Distribution - 威沙特分布是卡方分布的高维模拟。

参考

[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.

[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8

[3] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.

[4] Kreyszig, Erwin. Introductory Mathematical Statistics: Principles and Methods. New York: Wiley, 1970.

另请参阅

| | | | |

主题