多元正态分布

概述

多元正态分布是一元正态分布的双变量或多变量泛化。它是相关变量的随机向量分布，其中每个向量元素都具有一元正态分布。在最简单的情形下，各变量之间没有相关性，向量的元素是独立的一元正态随机变量。

由于它易于处理，因此多元正态分布通常用作多元数据的模型。

Statistics and Machine Learning Toolbox™ 提供了几个与多元正态分布相关的功能。

  • 使用 mvnrnd 从该分布中生成随机数。

  • 使用 mvnpdf 在特定值处计算概率密度函数 (pdf)。

  • 使用 mvncdf 在特定值处计算累积分布函数 (cdf)。

参数

多元正态分布使用下表中的参数。

参数描述一元正态对应参数
μ均值向量均值 μ（标量）
Σ协方差矩阵 - 对角线元素包含每个变量的方差，非对角线元素包含变量之间的协方差方差 σ2（标量）

请注意，在一维情况下，Σ 是方差，而不是标准差。有关一元正态分布参数的详细信息，请参阅参数。

概率密度函数

d 维多元正态分布的概率密度函数 (pdf) 是

y = f(x,μ,Σ) = 1|Σ|(2π)dexp(−12(x-μ) Σ-1(x-μ)')

，其中 x 和 μ 是 1×d 向量，而 Σ 是 d×d 对称正定矩阵。

请注意，Statistics and Machine Learning Toolbox：

  • 仅支持将奇异 Σ 用于随机向量生成。当 Σ 是奇异矩阵时，pdf 不能以相同的形式写入。

  • 使用 x 和 μ 作为行向量而不是列向量。

有关示例，请参阅二元正态分布 pdf。

累积分布函数

在 x 处计算的多元正态累积分布函数 (cdf) 定义为随机向量 v（以多元正态形式分布）位于上限由 x 定义的半无限矩形内的概率：

Pr{v(1)≤x(1),v(2)≤x(2),...,v(d)≤x(d)}.

尽管多元正态 cdf 没有封闭形式，但 mvncdf 能够以数值方式计算 cdf 值。

有关示例，请参阅二元正态分布 cdf。

示例

二元正态分布 pdf

打开实时脚本

计算并绘制具有参数 mu = [0 0] 和 Sigma = [0.25 0.3; 0.3 1] 的二元正态分布的 pdf。

定义参数 mu 和 Sigma。

mu = [0 0];
Sigma = [0.25 0.3; 0.3 1];

在二维空间中创建一个等间距点网格。

x1 = -3:0.2:3;
x2 = -3:0.2:3;
[X1,X2] = meshgrid(x1,x2);
X = [X1(:) X2(:)];

在网格点处计算正态分布的 pdf。

y = mvnpdf(X,mu,Sigma);
y = reshape(y,length(x2),length(x1));

绘制 pdf 值。

surf(x1,x2,y)
axis([-3 3 -3 3 0 0.4])
xlabel('x1')
ylabel('x2')
zlabel('Probability Density')

Figure contains an axes object. The axes object with xlabel x1, ylabel x2 contains an object of type surface.

二元正态分布 cdf

打开实时脚本

计算并绘制二元正态分布的 cdf。

定义均值向量 mu 和协方差矩阵 Sigma。

mu = [1 -1];
Sigma = [.9 .4; .4 .3];

在二维空间中创建一个包含 625 个等间距点的网格。

[X1,X2] = meshgrid(linspace(-1,3,25)',linspace(-3,1,25)');
X = [X1(:) X2(:)];

在网格点处计算正态分布的 cdf。

p = mvncdf(X,mu,Sigma);

绘制 cdf 值。

Z = reshape(p,25,25);
surf(X1,X2,Z)

Figure contains an axes object. The axes object contains an object of type surface.

矩形区域上的概率

打开实时脚本

计算二元正态分布单位正方形上的概率，并创建一个结果等高线图。

定义二元正态分布参数 mu 和 Sigma。

mu = [0 0];
Sigma = [0.25 0.3; 0.3 1];

计算单位正方形上的概率。

p = mvncdf([0 0],[1 1],mu,Sigma)
p = 
0.2097

为了可视化结果，首先需要在二维空间中创建一个等间距点网格。

x1 = -3:.2:3;
x2 = -3:.2:3;
[X1,X2] = meshgrid(x1,x2);
X = [X1(:) X2(:)];

然后，在网格点处计算正态分布的 pdf。

y = mvnpdf(X,mu,Sigma);
y = reshape(y,length(x2),length(x1));

最后，创建一个包含单位正方形的多元正态分布的等高线图。

contour(x1,x2,y,[0.0001 0.001 0.01 0.05 0.15 0.25 0.35])
xlabel('x')
ylabel('y')
line([0 0 1 1 0],[1 0 0 1 1],'Linestyle','--','Color','k')

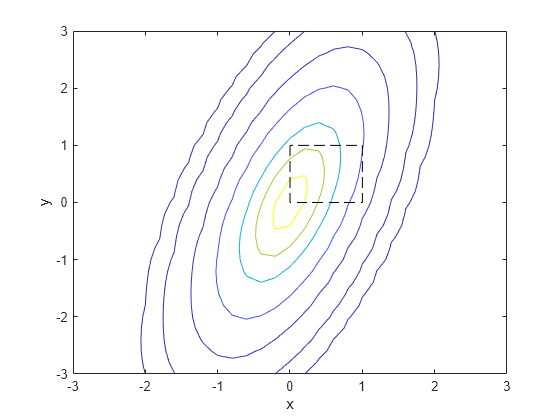
Figure contains an axes object. The axes object with xlabel x, ylabel y contains 2 objects of type contour, line.

计算多元累积概率需要比计算一元概率多很多的工作。默认情况下，mvncdf 函数计算的值小于完整计算机精度，并返回错误估计作为可选的第二个输出。查看这种情况下的错误估计。

[p,err] = mvncdf([0 0],[1 1],mu,Sigma)
p = 
0.2097

err = 
1.0000e-08

参考

[1] Kotz, S., N. Balakrishnan, and N. L. Johnson. Continuous Multivariate Distributions: Volume 1: Models and Applications. 2nd ed. New York: John Wiley & Sons, Inc., 2000.

另请参阅

| | |

主题