mvnpdf

多元正态概率密度函数

全页折叠

语法

y = mvnpdf(X)

y = mvnpdf(X,mu)

y = mvnpdf(X,mu,Sigma)

说明

y = mvnpdf(X) 返回一个 n×1 向量 y，其中包含具有零均值和单位协方差矩阵的 d 维多元正态分布的概率密度函数 (pdf) 值，在 n×d 矩阵 X 的每行处进行计算。有关详细信息，请参阅多元正态分布。

示例

y = mvnpdf(X,mu) 返回 X 中的点处的 pdf 值，其中 mu 确定每个关联的多元正态分布的均值。

示例

y = mvnpdf(X,mu,Sigma) 返回 X 中的点处的 pdf 值，其中 Sigma 确定每个关联的多元正态分布的协方差。

当您只想指定 Sigma 时，为 mu 指定 [] 以使用其默认值零。

示例

全部折叠

标准多元正态 pdf

打开实时脚本

在一组随机点处计算一个标准五维正态分布的 pdf。

从该标准五维正态分布中随机采样八个点。

mu = zeros(1,5);
Sigma = eye(5);
rng('default')  % For reproducibility
X = mvnrnd(mu,Sigma,8)

X = 8×5

    0.5377    3.5784   -0.1241    0.4889   -1.0689
    1.8339    2.7694    1.4897    1.0347   -0.8095
   -2.2588   -1.3499    1.4090    0.7269   -2.9443
    0.8622    3.0349    1.4172   -0.3034    1.4384
    0.3188    0.7254    0.6715    0.2939    0.3252
   -1.3077   -0.0631   -1.2075   -0.7873   -0.7549
   -0.4336    0.7147    0.7172    0.8884    1.3703
    0.3426   -0.2050    1.6302   -1.1471   -1.7115

在 X 中的各点处计算分布的 pdf。

y = mvnpdf(X)

找出 X 中 pdf 值最大的点。

[maxpdf,idx] = max(y)

maxpdf = 
0.0054

idx = 
5

maxPoint = X(idx,:)

maxPoint = 1×5

    0.3188    0.7254    0.6715    0.2939    0.3252

X 中的第五个点比任何其他随机选择的点具有更大的 pdf 值。

在不同点处计算的多元正态 pdf

打开实时脚本

创建六个三维正态分布，每个都有不同均值。在一个不同随机点处计算每个分布的 pdf。

指定分布的均值 mu 和协方差 Sigma。每个分布都有相同的协方差矩阵 - 单位矩阵。

firstDim = (1:6)';
mu = repmat(firstDim,1,3)

mu = 6×3

     1     1     1
     2     2     2
     3     3     3
     4     4     4
     5     5     5
     6     6     6

Sigma = eye(3)

Sigma = 3×3

     1     0     0
     0     1     0
     0     0     1

从六个分布的每个分布中随机采样一次。

rng('default')  % For reproducibility
X = mvnrnd(mu,Sigma)

X = 6×3

    1.5377    0.5664    1.7254
    3.8339    2.3426    1.9369
    0.7412    6.5784    3.7147
    4.8622    6.7694    3.7950
    5.3188    3.6501    4.8759
    4.6923    9.0349    7.4897

在 X 中的各点处计算分布的 pdf。第一个分布的 pdf 在点 X(1,:) 处计算，第二个分布的 pdf 在点 X(2,:) 处计算，依此类推。

y = mvnpdf(X,mu)

多元正态 pdf

打开实时脚本

计算一个二维正态分布在一组给定点处的 pdf。

指定该分布的均值 mu 和协方差 Sigma。

mu = [1 -1];
Sigma = [0.9 0.4; 0.4 0.3];

从分布中随机采样 100 次。将 X 指定为采样点矩阵。

rng('default')  % For reproducibility
X = mvnrnd(mu,Sigma,100);

在 X 中的各点处计算分布的 pdf。

y = mvnpdf(X,mu,Sigma);

绘制概率密度值。

scatter3(X(:,1),X(:,2),y)
xlabel('X1')
ylabel('X2')
zlabel('Probability Density')

Figure contains an axes object. The axes object with xlabel X1, ylabel X2 contains an object of type scatter.

在同一点处计算的多元正态 pdf

打开实时脚本

创建十个不同的五维正态分布，并比较它们在一个指定点处的 pdf 值。

将维度 n 和 d 分别设置为等于 10 和 5。

n = 10;
d = 5;

指定多元正态分布的均值 mu 和协方差 Sigma。让所有分布具有相同的均值向量，但协方差矩阵不同。

mu = ones(1,d)

mu = 1×5

     1     1     1     1     1

mat = eye(d);
nMat = repmat(mat,1,1,n);
var = reshape(1:n,1,1,n);
Sigma = nMat.*var;

显示 Sigma 中的前两个协方差矩阵。

Sigma(:,:,1:2)

ans = 
ans(:,:,1) =

     1     0     0     0     0
     0     1     0     0     0
     0     0     1     0     0
     0     0     0     1     0
     0     0     0     0     1


ans(:,:,2) =

     2     0     0     0     0
     0     2     0     0     0
     0     0     2     0     0
     0     0     0     2     0
     0     0     0     0     2

将 x 设为五维空间中的一个随机点。

rng('default')  % For reproducibility
x = normrnd(0,1,1,5)

x = 1×5

    0.5377    1.8339   -2.2588    0.8622    0.3188

计算十个分布中每个分布在 x 处的 pdf。

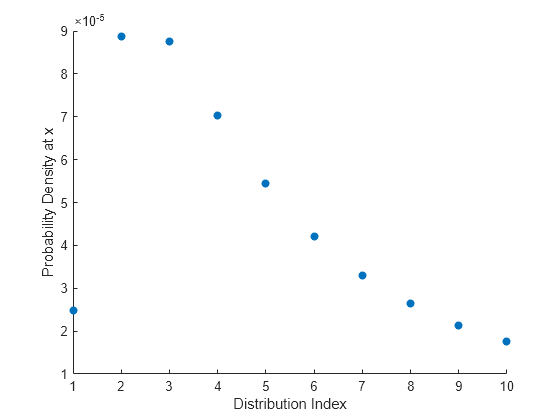
y = mvnpdf(x,mu,Sigma)

绘制结果。

scatter(1:n,y,'filled')
xlabel('Distribution Index')
ylabel('Probability Density at x')

Figure contains an axes object. The axes object with xlabel Distribution Index, ylabel Probability Density at x contains an object of type scatter.

输入参数

全部折叠

`X` — 计算点
数值向量 | 数值矩阵

计算点，指定为 1×d 数值向量或 n×d 数值矩阵，其中 n 是正整数标量，d 是一个多元正态分布的维度。X 的行对应于观测值（或点），列对应于变量（或坐标）。

如果 X 是向量，则 mvnpdf 复制它以匹配 mu 的头部维度或 Sigma 的尾部维度。

数据类型: single | double

`mu` — 多元正态分布的均值
零向量 (默认) | 数值向量 | 数值矩阵

多元正态分布的均值，指定为 1×d 数值向量或 n×d 数值矩阵。

如果 mu 是向量，则 mvnpdf 复制该向量以匹配 Sigma 的尾部维度。
如果 mu 是矩阵，则 mu 的每行均为单个多元正态分布的均值向量。

数据类型: single | double

`Sigma` — 多元正态分布的协方差
单位矩阵 (默认) | 对称正定矩阵 | 数值数组

多元正态分布的协方差，指定为 d×d 对称正定矩阵或 d×d×n 数值数组。

如果 Sigma 是矩阵，则 mvnpdf 复制该矩阵以匹配 mu 中的行数。
如果 Sigma 是数组，则 Sigma 的每页 Sigma(:,:,i) 均为单个多元正态分布的协方差矩阵，因此它是对称正定矩阵。

如果这些协方差矩阵是对角矩阵，即对角线上为方差且对角线外为零协方差，您也可以将 Sigma 指定为 1×d 的向量或只包含对角线元素的 1×d×n 的数组。

数据类型: single | double

输出参量

全部折叠

`y` — pdf 值
数值向量

pdf 值，以 n×1 数值向量形式返回，其中 n 是以下值之一：

如果 X 是矩阵，则为 X 中的行数
如果 X 是向量，则为复制 X 的次数

如果 X 是矩阵、mu 是矩阵，而 Sigma 是数组，则 mvnpdf 使用 X(i,:)、mu(i,:) 和 Sigma(:,:,i) 来计算 y(i)。

详细信息

全部折叠

多元正态分布

多元正态分布是一元正态分布的双变量或多变量泛化。它有两个参数，即均值向量 μ 和协方差矩阵 Σ，它们类似于一元正态分布的均值和方差参数。Σ 的对角线元素包含每个变量的方差，而 Σ 的非对角线元素包含变量之间的协方差。

d 维多元正态分布的概率密度函数 (pdf) 是

$y = f (x, μ, Σ) = \frac{1}{\sqrt{| Σ | {(2 π)}^{d}}} \exp (- \frac{1}{2} (x - μ) Σ^{-1} (x - μ)')$

其中 x 和 μ 是 1×d 向量，而 Σ 是 d×d 对称正定矩阵。只有 mvnrnd 允许半正定 Σ 矩阵，它们可以是奇异矩阵。当 Σ 是奇异矩阵时，pdf 不能有相同的形式。

在 x 处计算的多元正态累积分布函数 (cdf) 是随机向量 v（以多元正态形式分布）位于上限由 x 定义的半无限矩形内的概率：

$\Pr {v (1) \leq x (1), v (2) \leq x (2), ..., v (d) \leq x (d)} .$

尽管多元正态 cdf 没有封闭形式，但 mvncdf 能够以数值方式计算 cdf 值。

提示

在一维情况下，Sigma 是方差，而不是标准差。例如，mvnpdf(1,0,4) 与 normpdf(1,0,2) 相同，其中 4 是方差，2 是标准差。

参考

[1] Kotz, S., N. Balakrishnan, and N. L. Johnson. Continuous Multivariate Distributions: Volume 1: Models and Applications. 2nd ed. New York: John Wiley & Sons, Inc., 2000.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

此函数完全支持 GPU 数组。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

另请参阅

mvncdf | mvnrnd | normpdf

主题

多元正态分布

mvnpdf

语法

说明

示例

标准多元正态 pdf

在不同点处计算的多元正态 pdf

多元正态 pdf

在同一点处计算的多元正态 pdf

输入参数

X — 计算点 数值向量 | 数值矩阵

mu — 多元正态分布的均值 零向量 (默认) | 数值向量 | 数值矩阵

Sigma — 多元正态分布的协方差 单位矩阵 (默认) | 对称正定矩阵 | 数值数组

输出参量

y — pdf 值 数值向量

详细信息

多元正态分布

提示

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

版本历史记录

另请参阅

主题

`X` — 计算点
数值向量 | 数值矩阵

`mu` — 多元正态分布的均值
零向量 (默认) | 数值向量 | 数值矩阵

`Sigma` — 多元正态分布的协方差
单位矩阵 (默认) | 对称正定矩阵 | 数值数组

`y` — pdf 值
数值向量

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。