Main Content

泊松分布

概述

泊松分布是单参数曲线族，它对随机事件的发生次数进行建模。此分布适用于涉及计算在给定的时间段、距离、面积等范围内发生随机事件的次数的应用情形。应用泊松分布的例子包括盖革计数器每秒咔嗒的次数、每小时走入商店的人数，以及网络上每分钟的丢包数。

Statistics and Machine Learning Toolbox™ 提供了几种处理泊松分布的方法。

  • 可通过对样本数据进行概率分布拟合或通过指定参数值来创建概率分布对象 PoissonDistribution。然后使用对象函数来计算分布、生成随机数等。

  • 使用分布拟合器以交互方式处理泊松分布。您可以从该 App 中导出对象并使用对象函数。

  • 将分布特定的函数（poisscdf、poisspdf、poissinv、poisstat、poissfit、poissrnd）与指定的分布参数结合使用。分布特定的函数可以接受多个泊松分布的参数。

  • 将一般分布函数（cdf、icdf、pdf、random）与指定的分布名称 ('Poisson') 和参数结合使用。

参数

泊松分布使用以下参数。

参数描述支持
lambda (λ)均值λ≥0

参数 λ 也等于泊松分布的方差。

参数为 λ1 和 λ2 的两个泊松随机变量之和是一个参数为 λ = λ1 + λ2 的泊松随机变量。

概率密度函数

泊松分布的概率密度函数 (pdf) 是

f(x|λ)=λxx!e−λ ; x=0,1,2,…,∞ .

结果是随机事件发生的概率正好是 x。对于离散分布，pdf 也称为概率质量函数 (pmf)。

有关示例，请参阅计算泊松分布 pdf。

累积分布函数

泊松分布的累积分布函数 (cdf) 为

p=F(x|λ)=e−λ∑i=0floor(x)λii!.

结果是随机事件发生的概率最多为 x。

有关示例，请参阅计算泊松分布 cdf。

示例

计算泊松分布 pdf

打开实时脚本

计算参数 lambda = 4 的泊松分布的 pdf。 

x = 0:15;
y = poisspdf(x,4);

用宽度为 1 的条形绘制 pdf。

figure
bar(x,y,1)
xlabel('Observation')
ylabel('Probability')

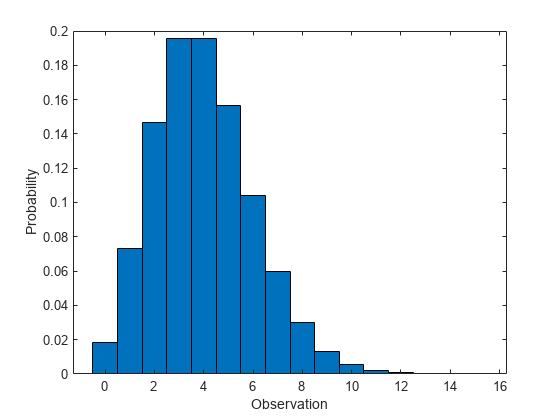
Figure contains an axes object. The axes object with xlabel Observation, ylabel Probability contains an object of type bar.

计算泊松分布 cdf

打开实时脚本

计算参数 lambda = 4 的泊松分布的 cdf。 

x = 0:15;
y = poisscdf(x,4);

绘制 cdf。 

figure
stairs(x,y)
xlabel('Observation')
ylabel('Cumulative Probability')

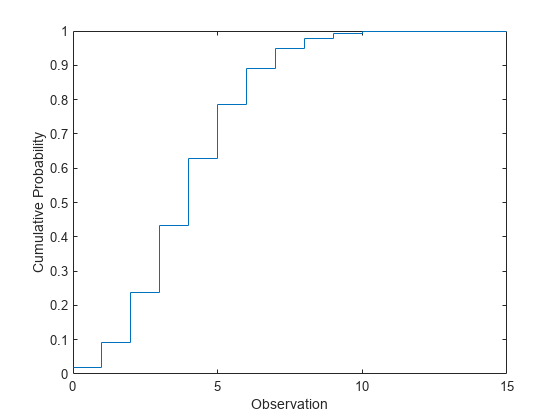
Figure contains an axes object. The axes object with xlabel Observation, ylabel Cumulative Probability contains an object of type stair.

比较泊松分布和正态分布的 pdf

打开实时脚本

当 lambda 较大时，泊松分布可以用均值为 lambda 和方差为 lambda 的正态分布来逼近。

计算参数 lambda = 50 的泊松分布的 pdf。

lambda = 50;
x1 = 0:100;
y1 = poisspdf(x1,lambda);

计算对应正态分布的 pdf。

mu = lambda;
sigma = sqrt(lambda);
x2 = 0:0.1:100;
y2 = normpdf(x2,mu,sigma);

在同一个轴上绘制这些 pdf。

figure
bar(x1,y1,1)
hold on
plot(x2,y2,'LineWidth',2)
xlabel('Observation')
ylabel('Probability')
title('Poisson and Normal pdfs')
legend('Poisson Distribution','Normal Distribution','location','northwest')
hold off

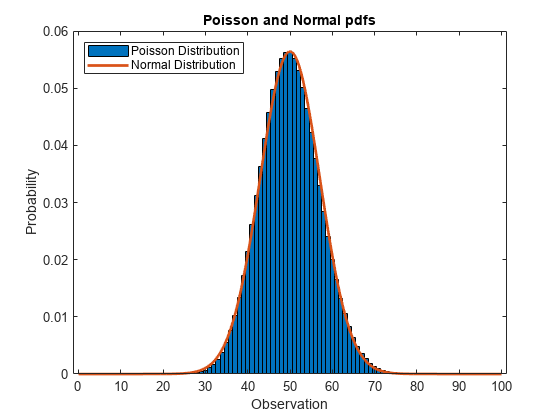
Figure contains an axes object. The axes object with title Poisson and Normal pdfs, xlabel Observation, ylabel Probability contains 2 objects of type bar, line. These objects represent Poisson Distribution, Normal Distribution.

正态分布的 pdf 高度逼近泊松分布的 pdf。

相关分布

  • Binomial Distribution - 二项分布是双参数离散分布，它对 N 次独立试验的成功次数进行计数，成功概率为 p。泊松分布是二项分布的极限情况，其中 N 趋向无穷，p 趋向零，而 Np = λ。请参阅Compare Binomial and Poisson Distribution pdfs。

  • Exponential Distribution - 指数分布是具有参数 μ（均值）的单参数连续分布。泊松分布对随机事件在给定时间内发生的次数计数进行建模。在这种模型中，事件的时间间隔服从均值为 1λ 的指数分布。

  • 正态分布 - 正态分布是双参数连续分布，具有参数 μ（均值）和 σ（标准差）。当 λ 较大时，泊松分布可以用具有 μ = λ 和 σ2 = λ 的正态分布来逼近。请参阅比较泊松分布和正态分布的 pdf。

参考

[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.

[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8

[3] Evans, Merran, Nicholas Hastings, and Brian Peacock. Statistical Distributions. 2nd ed. New York: J. Wiley, 1993.

[4] Loader, Catherine. Fast and Accurate Computation of Binomial Probabilities. July 9, 2000.

另请参阅

| | | | | |

相关主题