基于问题的优化实时编辑器任务快速入门

此示例脚本帮助您使用基于问题的优化实时编辑器任务进行优化或方程求解。请根据您自己的具体问题修改脚本。

该脚本求解具有非线性约束的非线性优化问题：

最小化 $r o s e n b r o c k (x, y, a) = \log (1 + a (y - x^{2})^{2} + (1 - x)^{2})$ 且需满足约束 $x^{2} + y^{2} \leq 1$ ，其中 $a = 100$ ，且初始点 $x 0$ 为 $x = - 2, y = 2$ 。另外，施加边界 $- 3 \leq x \leq 3$ 、 $- 2 \leq y \leq 9$ 。

目标函数的代码在此脚本的末尾。

包括参数或数据

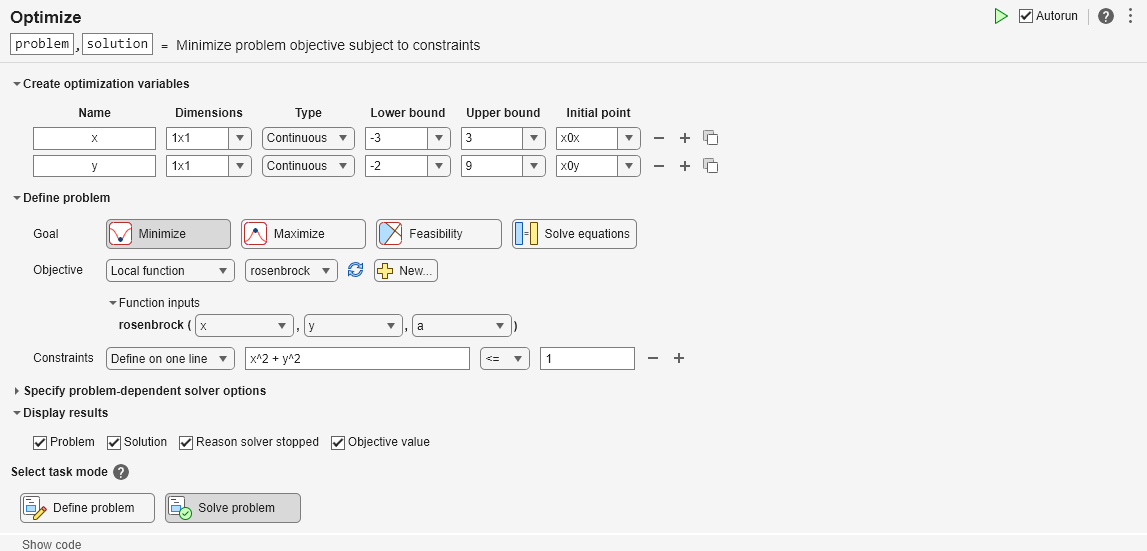
通常，您有数据或值要传递给求解器。将这些值放入输入节（其中显示 x0x 和 x0y），并通过选择节 > 运行节或按 Control+Enter 来运行该节。

设置优化的初始点分量 x0x 和 x0y 以及缩放系数 a。

x0x = -2;
x0y = 2;
a = 100;

在继续之前，通过运行此节，将这些值和其他的问题数据放入工作区中。

优化实时编辑器任务

通常，您可以通过在实时编辑器选项卡中选择任务 > 优化，或在插入选项卡中选择任务 > 优化，将优化实时编辑器任务放入脚本中。然后您将看到以下选择项（这只是图示，并非真实任务）：

要获取基于问题的任务，请点击基于问题(推荐)。

以下基于问题的任务已填充了变量、目标和约束。请针对您的问题修改它，或按原样运行它，看看任务如何执行。要修改问题，请点击任务底部的定义问题按钮。要运行该任务，请点击任务底部的求解问题按钮。

  OptimizationProblem : 

	Solve for:
       x, y

	minimize :
       log(((1 + (100 .* (y - x.^2).^2)) + (1 - x).^2))


	subject to :
       (x.^2 + y.^2) <= 1

	variable bounds:
       -3 <= x <= 3

       -2 <= y <= 9

Solving problem using fmincon.

Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

<stopping criteria details>

solution = struct with fields:
    x: 0.7864
    y: 0.6177

reasonSolverStopped = 
    OptimalSolution

objectiveValue = 
0.0447

解释结果

该任务调用 solve，后者调用 fmincon 来求解问题。任务顶部显示解以 solution 结构体形式返回。给出的解 x = 0.7864 和 y = 0.6177 满足约束 $x^{2} + y^{2} \leq 1$ ，如以下计算所示。

solution.x^2 + solution.y^2

ans = 
1.0000

求解器在停止时报告退出条件 OptimalSolution。要解释此条件，请查看 fmincon 求解器的 exitflag 输出参量。该描述说明“一阶最优性测度小于 options.OptimalityTolerance，最大约束违反值小于 options.ConstraintTolerance”。换句话说，解是可行的局部最小值。

在解处的目标函数值是 0.0457。这是可行点中最小的目标函数值。

辅助函数

以下代码会创建 rosenbrock 辅助函数。

function objective = rosenbrock(x,y,a)
% This function should return a scalar representing an optimization objective.

% Example: Concession stand profit
% revenue = 3*soda + 5*popcorn + 2*candy;
% cost = 1*soda + 2*popcorn + 0.75*candy;
% objective = revenue - cost; % profit

% Edit the lines below with your calculations.
objective = log(1 + a*(y - x^2)^2 + (1 - x)^2);
end

另请参阅

优化