在 GPU 上对 A\b 进行基准测试
这个示例研究如何在 GPU 上对线性系统的求解进行基准测试。用于解决 x 中的 A*x = b 的 MATLAB® 代码非常简单。最常见的是,我们使用矩阵左除法(也称为 mldivide 或反斜杠运算符 (\) 来计算 x(即 x = A\b)。
相关示例:
基准测试 A\ b 使用分布式数组。
本示例中显示的代码可以在以下函数中找到:
function results = paralleldemo_gpu_backslash(maxMemory)
选择适合计算的矩阵大小非常重要。我们可以通过指定 CPU 和 GPU 可用的系统内存量(以 GB 为单位)来实现这一点。默认值仅基于 GPU 上可用的内存量,您可以指定适合您系统的值。
if nargin == 0 g = gpuDevice; maxMemory = 0.4*g.AvailableMemory/1024^3; end
基准测试函数
我们希望对矩阵左除法 (\) 进行基准测试,而不是对 CPU 和 GPU 之间传输数据的成本、创建矩阵所需的时间或其他参数进行基准测试。因此,我们将数据生成与线性系统的求解分开,只测量后者所需的时间。
function [A, b] = getData(n, clz) fprintf('Creating a matrix of size %d-by-%d.\n', n, n); A = rand(n, n, clz) + 100*eye(n, n, clz); b = rand(n, 1, clz); end function time = timeSolve(A, b, waitFcn) tic; x = A\b; %#ok<NASGU> We don't need the value of x. waitFcn(); % Wait for operation to complete. time = toc; end
选择问题大小
与许多其他并行算法一样,并行求解线性系统的性能很大程度上取决于矩阵大小。如在其他示例中所见,例如基准测试 A\ b,我们比较了不同矩阵大小的算法的性能。
% Declare the matrix sizes to be a multiple of 1024. maxSizeSingle = floor(sqrt(maxMemory*1024^3/4)); maxSizeDouble = floor(sqrt(maxMemory*1024^3/8)); step = 1024; if maxSizeDouble/step >= 10 step = step*floor(maxSizeDouble/(5*step)); end sizeSingle = 1024:step:maxSizeSingle; sizeDouble = 1024:step:maxSizeDouble;
比较性能:Gigaflops
我们使用每秒浮点运算次数作为性能衡量标准,因为这使我们能够比较不同矩阵大小的算法的性能。
给定一个矩阵大小,基准测试函数会创建矩阵 A 和右侧 b 一次,然后求解 A\b 几次以准确测量所需时间。我们使用 HPC Challenge 的浮点运算计数,因此对于 n×n 矩阵,我们将浮点运算计为 2/3*n^3 + 3/2*n^2。
该函数通过句柄传递给“等待”函数。在 CPU 上,此函数不执行任何操作。在 GPU 上,此函数等待所有待处理的操作完成。以这种方式等待可确保准确的时间。
function gflops = benchFcn(A, b, waitFcn) numReps = 3; time = inf; % We solve the linear system a few times and calculate the Gigaflops % based on the best time. for itr = 1:numReps tcurr = timeSolve(A, b, waitFcn); time = min(tcurr, time); end % Measure the overhead introduced by calling the wait function. tover = inf; for itr = 1:numReps tic; waitFcn(); tcurr = toc; tover = min(tcurr, tover); end % Remove the overhead from the measured time. Don't allow the time to % become negative. time = max(time - tover, 0); n = size(A, 1); flop = 2/3*n^3 + 3/2*n^2; gflops = flop/time/1e9; end % The CPU doesn't need to wait: this function handle is a placeholder. function waitForCpu() end % On the GPU, to ensure accurate timing, we need to wait for the device % to finish all pending operations. function waitForGpu(theDevice) wait(theDevice); end
执行基准测试
完成所有设置后,执行基准测试就很简单了。然而,计算可能需要很长时间才能完成,因此我们在完成每个矩阵大小的基准测试时打印一些中间状态信息。我们还将遍历所有矩阵大小的循环封装在一个函数中,以对单精度和双精度计算进行基准测试。
function [gflopsCPU, gflopsGPU] = executeBenchmarks(clz, sizes) fprintf(['Starting benchmarks with %d different %s-precision ' ... 'matrices of sizes\nranging from %d-by-%d to %d-by-%d.\n'], ... length(sizes), clz, sizes(1), sizes(1), sizes(end), ... sizes(end)); gflopsGPU = zeros(size(sizes)); gflopsCPU = zeros(size(sizes)); gd = gpuDevice; for i = 1:length(sizes) n = sizes(i); [A, b] = getData(n, clz); gflopsCPU(i) = benchFcn(A, b, @waitForCpu); fprintf('Gigaflops on CPU: %f\n', gflopsCPU(i)); A = gpuArray(A); b = gpuArray(b); gflopsGPU(i) = benchFcn(A, b, @() waitForGpu(gd)); fprintf('Gigaflops on GPU: %f\n', gflopsGPU(i)); end end
然后我们以单精度和双精度执行基准测试。
[cpu, gpu] = executeBenchmarks('single', sizeSingle); results.sizeSingle = sizeSingle; results.gflopsSingleCPU = cpu; results.gflopsSingleGPU = gpu; [cpu, gpu] = executeBenchmarks('double', sizeDouble); results.sizeDouble = sizeDouble; results.gflopsDoubleCPU = cpu; results.gflopsDoubleGPU = gpu;
Starting benchmarks with 7 different single-precision matrices of sizes ranging from 1024-by-1024 to 19456-by-19456. Creating a matrix of size 1024-by-1024. Gigaflops on CPU: 43.805496 Gigaflops on GPU: 78.474002 Creating a matrix of size 4096-by-4096. Gigaflops on CPU: 96.459635 Gigaflops on GPU: 573.278854 Creating a matrix of size 7168-by-7168. Gigaflops on CPU: 184.997657 Gigaflops on GPU: 862.755636 Creating a matrix of size 10240-by-10240. Gigaflops on CPU: 204.404384 Gigaflops on GPU: 978.362901 Creating a matrix of size 13312-by-13312. Gigaflops on CPU: 218.773070 Gigaflops on GPU: 1107.983667 Creating a matrix of size 16384-by-16384. Gigaflops on CPU: 233.529176 Gigaflops on GPU: 1186.423754 Creating a matrix of size 19456-by-19456. Gigaflops on CPU: 241.482550 Gigaflops on GPU: 1199.151846 Starting benchmarks with 5 different double-precision matrices of sizes ranging from 1024-by-1024 to 13312-by-13312. Creating a matrix of size 1024-by-1024. Gigaflops on CPU: 34.902918 Gigaflops on GPU: 72.191488 Creating a matrix of size 4096-by-4096. Gigaflops on CPU: 74.458136 Gigaflops on GPU: 365.339897 Creating a matrix of size 7168-by-7168. Gigaflops on CPU: 93.313782 Gigaflops on GPU: 522.514165 Creating a matrix of size 10240-by-10240. Gigaflops on CPU: 104.219804 Gigaflops on GPU: 628.301313 Creating a matrix of size 13312-by-13312. Gigaflops on CPU: 108.826886 Gigaflops on GPU: 681.881032
绘制性能图
我们现在可以绘制结果,并比较 CPU 和 GPU 上的单精度和双精度性能。
首先,我们看一下单精度反斜杠运算符的性能。
fig = figure; ax = axes('parent', fig); plot(ax, results.sizeSingle, results.gflopsSingleGPU, '-x', ... results.sizeSingle, results.gflopsSingleCPU, '-o') grid on; legend('GPU', 'CPU', 'Location', 'NorthWest'); title(ax, 'Single-precision performance') ylabel(ax, 'Gigaflops'); xlabel(ax, 'Matrix size'); drawnow;
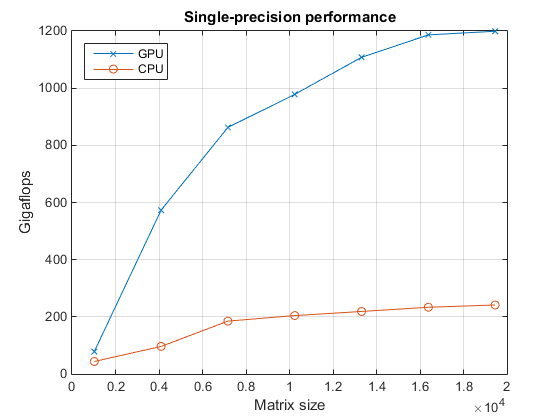
现在,我们来看看双精度反斜杠运算符的性能。
fig = figure; ax = axes('parent', fig); plot(ax, results.sizeDouble, results.gflopsDoubleGPU, '-x', ... results.sizeDouble, results.gflopsDoubleCPU, '-o') legend('GPU', 'CPU', 'Location', 'NorthWest'); grid on; title(ax, 'Double-precision performance') ylabel(ax, 'Gigaflops'); xlabel(ax, 'Matrix size'); drawnow;
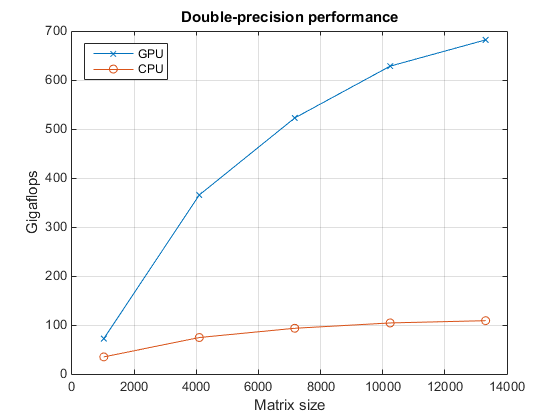
最后,我们来比较一下 GPU 与 CPU 之间反斜杠运算符的加速情况。
speedupDouble = results.gflopsDoubleGPU./results.gflopsDoubleCPU; speedupSingle = results.gflopsSingleGPU./results.gflopsSingleCPU; fig = figure; ax = axes('parent', fig); plot(ax, results.sizeSingle, speedupSingle, '-v', ... results.sizeDouble, speedupDouble, '-*') grid on; legend('Single-precision', 'Double-precision', 'Location', 'SouthEast'); title(ax, 'Speedup of computations on GPU compared to CPU'); ylabel(ax, 'Speedup'); xlabel(ax, 'Matrix size'); drawnow;

end
ans =
sizeSingle: [1024 4096 7168 10240 13312 16384 19456]
gflopsSingleCPU: [1x7 double]
gflopsSingleGPU: [1x7 double]
sizeDouble: [1024 4096 7168 10240 13312]
gflopsDoubleCPU: [34.9029 74.4581 93.3138 104.2198 108.8269]
gflopsDoubleGPU: [72.1915 365.3399 522.5142 628.3013 681.8810]
另请参阅
gpuArray | gpuDevice | mldivide