基准测试 A`\` b

打开脚本

此示例说明如何对集群上的线性系统求解进行基准测试。用于解决 x 中的 A*x = b 的 MATLAB® 代码非常简单。最常见的是，使用矩阵左除法（也称为 mldivide 或反斜杠运算符 (\) 来计算 x（即 x = A\b）。然而，对集群上矩阵左除法的性能进行基准测试并不是那么简单。

基准测试最具挑战性的方面之一是避免陷入寻找代表系统整体性能的单一数字的陷阱。我们将查看性能曲线，这可能有助于您识别集群上的性能瓶颈，甚至可能帮助您了解如何对代码进行基准测试并从结果中得出有意义的结论。

避免开销

为了准确衡量我们解决线性系统的能力，我们需要消除任何可能的开销来源。这包括获取当前并行池并暂时禁用死锁检测功能。

p = gcp;
if isempty(p)
    error('pctexample:backslashbench:poolClosed', ...
        ['This example requires a parallel pool. ' ...
         'Manually start a pool using the parpool command or set ' ...
         'your parallel settings to automatically start a pool.']);
end
poolSize = p.NumWorkers;
pctRunOnAll 'mpiSettings(''DeadlockDetection'', ''off'');'

Starting parallel pool (parpool) using the 'bigMJS' profile ... connected to 12 workers.

基准测试函数

我们希望对矩阵左除法 (\) 进行基准测试，而不是进入 spmd 代码块的成本、创建矩阵所需的时间或其他参数。因此，我们将数据生成与线性系统的求解分开，只测量后者所需的时间。我们使用二维块循环协同分布器生成输入数据，因为这是解决线性系统的最有效的分配方案。我们的基准测试包括测量所有工作单元完成解决线性系统 A*x = b 所需的时间。再次，我们尝试消除任何可能的开销来源。

function [A, b] = getData(n)
    fprintf('Creating a matrix of size %d-by-%d.\n', n, n);
    spmd
        % Use the codistributor that usually gives the best performance
        % for solving linear systems.
        codistr = codistributor2dbc(codistributor2dbc.defaultLabGrid, ...
                                    codistributor2dbc.defaultBlockSize, ...
                                    'col');
        A = codistributed.rand(n, n, codistr);
        b = codistributed.rand(n, 1, codistr);
    end
end

function time = timeSolve(A, b)
    spmd
        tic;
        x = A\b; %#ok<NASGU> We don't need the value of x.
        time = gop(@max, toc); % Time for all to complete.
    end
    time = time{1};
end

选择问题大小

与大量其他并行算法一样，并行求解线性系统的性能很大程度上取决于矩阵大小。因此，我们的先验预期是，计算结果如下：

对于小矩阵来说效率有点低
对于大型矩阵来说非常有效
如果矩阵太大，无法放入系统内存，并且操作系统开始将内存交换到磁盘，则效率低下

因此，对多个不同矩阵大小的计算进行计时很重要，以便了解在这种情况下“小”、“大”和“太大”的含义。根据之前的试验，我们预计：

矩阵“太小”，大小不能达到 1000×1000
“大型”矩阵占用每个工作单元可用内存的略少于 45%
“过大”矩阵占用了每个工作单元可用的系统内存的 50% 或更多

这些都是启发式方法，并且精确的值可能会在版本之间发生变化。因此，我们使用涵盖整个范围的矩阵大小并验证预期性能非常重要。

请注意，通过根据工作单元数量改变问题规模，我们采用了弱扩展。其他基准测试示例，例如使用二十一点对 PARFOR 进行简单基准测试和对集群上的独立作业进行基准测试，也采用了弱扩展。由于这些示例对并行计算任务进行了基准测试，因此它们的弱扩展性包括使迭代次数与工作单元数量成比例。然而，这个示例是对数据并行计算的基准测试，所以我们将矩阵的上限与工作单元数量联系起来。

% Declare the matrix sizes ranging from 1000-by-1000 up to 45% of system
% memory available to each worker.
maxMemUsagePerWorker = 0.45*memoryPerWorker*1024^3; % In bytes.
maxMatSize = round(sqrt(maxMemUsagePerWorker*poolSize/8));
matSize = round(linspace(1000, maxMatSize, 5));

比较性能：Gigaflops

我们使用每秒浮点运算次数作为性能衡量标准，因为这使我们能够比较不同矩阵大小和不同工作单元数量的算法的性能。如果我们成功测试了足够广泛的矩阵大小范围内的矩阵左除法的性能，我们预计性能图将类似于以下内容：

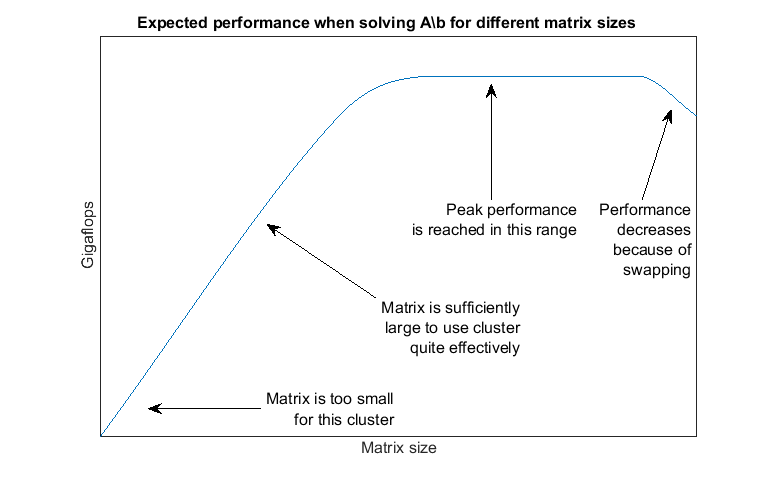
通过生成这样的图，我们可以回答以下问题：

最小矩阵是否太小以致于性能较差？
当矩阵太大以至于占据系统总内存的 45％时，性能是否下降？
对于给定数量的工作单元，我们可能实现的最佳绩效是什么？
对于哪种规模的矩阵，16 个工作单元的表现会比 8 个工作单元更好？
系统内存是否限制了峰值性能？

给定一个矩阵大小，基准测试函数会创建矩阵 A 和右侧 b 一次，然后多次求解 A\b 以准确测量所需时间。我们使用 HPC Challenge 的浮点运算计数，因此对于 n×n 矩阵，我们将浮点运算计为 2/3*n^3 + 3/2*n^2。

function gflops = benchFcn(n)
    numReps = 3;
    [A, b] = getData(n);
    time = inf;
    % We solve the linear system a few times and calculate the Gigaflops
    % based on the best time.
    for itr = 1:numReps
        tcurr = timeSolve(A, b);
        if itr == 1
            fprintf('Execution times: %f', tcurr);
        else
            fprintf(', %f', tcurr);
        end
        time = min(tcurr, time);
    end
    fprintf('\n');
    flop = 2/3*n^3 + 3/2*n^2;
    gflops = flop/time/1e9;
end

执行基准测试

完成所有设置后，执行基准测试就很简单了。然而，计算可能需要很长时间才能完成，因此我们在完成每个矩阵大小的基准测试时打印一些中间状态信息。

fprintf(['Starting benchmarks with %d different matrix sizes ranging\n' ...
         'from %d-by-%d to %d-by-%d.\n'], ...
        length(matSize), matSize(1), matSize(1), matSize(end), ...
        matSize(end));
gflops = zeros(size(matSize));
for i = 1:length(matSize)
    gflops(i) = benchFcn(matSize(i));
    fprintf('Gigaflops: %f\n\n', gflops(i));
end
results.matSize = matSize;
results.gflops = gflops;

Starting benchmarks with 5 different matrix sizes ranging
from 1000-by-1000 to 76146-by-76146.
Creating a matrix of size 1000-by-1000.
Analyzing and transferring files to the workers ...done.
Execution times: 1.038931, 0.592114, 0.575135
Gigaflops: 1.161756

Creating a matrix of size 19787-by-19787.
Execution times: 119.402579, 118.087116, 119.323904
Gigaflops: 43.741681

Creating a matrix of size 38573-by-38573.
Execution times: 552.256063, 549.088060, 555.753578
Gigaflops: 69.685485

Creating a matrix of size 57360-by-57360.
Execution times: 3580.232186, 3726.588242, 3113.261810
Gigaflops: 40.414533

Creating a matrix of size 76146-by-76146.
Execution times: 9261.720799, 9099.777287, 7968.750495
Gigaflops: 36.937936

绘制性能图

我们现在可以绘制结果，并与上面显示的预期图进行比较。

fig = figure;
ax = axes('parent', fig);
plot(ax, matSize/1000, gflops);
lines = ax.Children;
lines.Marker = '+';
ylabel(ax, 'Gigaflops')
xlabel(ax, 'Matrix size in thousands')
titleStr = sprintf(['Solving A\\b for different matrix sizes on ' ...
                    '%d workers'], poolSize);
title(ax, titleStr, 'Interpreter', 'none');

如果基准测试结果不如您预期的那样好，请考虑以下几点：

底层实现使用了 ScaLAPACK，其有着高性能的声誉。因此，算法或库不太可能导致效率低下，而是使用方式导致的，如下所述。
如果矩阵对于您的集群来说太小或太大，那么最终的性能就会很差。
如果网络通信速度慢，性能将受到严重影响。
如果 CPU 和网络通信都非常快，但内存量有限，则您可能无法使用足够大的矩阵进行基准测试以充分利用可用的 CPU 和网络带宽。
为了获得最佳性能，重要的是使用适合您的网络设置的 MPI 版本，并让工作单元以尽可能多的通信通过共享内存进行的方式运行。然而，解释如何识别和解决这些类型的问题超出了本示例的范围。

比较不同数量的工作单元

现在，我们通过查看使用不同数量的工作单元运行此示例所获得的数据来了解如何比较不同数量的工作单元。该数据是在与上述不同的集群上获得的。

其他示例，如对集群上的独立作业进行基准测试已经解释过，在对不同数量的工作单元进行并行测试并行算法时，通常采用弱扩展。也就是说，随着工作单元数量的增加，问题规模也会相应增加。对于矩阵左除法，我们必须格外小心，因为除法的性能很大程度上取决于矩阵的大小。以下代码针对我们测试过的所有矩阵大小和所有不同数量的工作单元创建了以 Gigaflops 为单位的性能图，因为它为我们提供了此特定集群上矩阵左除法的性能特征的最详细图像。

s = load('pctdemo_data_backslash.mat', 'workers4', 'workers8', ...
         'workers16', 'workers32', 'workers64');
fig = figure;
ax = axes('parent', fig);
plot(ax, s.workers4.matSize./1000, s.workers4.gflops, ...
     s.workers8.matSize./1000, s.workers8.gflops, ...
     s.workers16.matSize./1000, s.workers16.gflops, ...
     s.workers32.matSize./1000, s.workers32.gflops, ...
     s.workers64.matSize./1000, s.workers64.gflops);
lines = ax.Children;
set(lines, {'Marker'}, {'+'; 'o'; 'v'; '.'; '*'});
ylabel(ax, 'Gigaflops')
xlabel(ax, 'Matrix size in thousands')
title(ax, ...
      'Comparison data for solving A\\b on different numbers of workers');
legend('4 workers', '8 workers', '16 workers', '32 workers',  ...
       '64 workers', 'location', 'NorthWest');

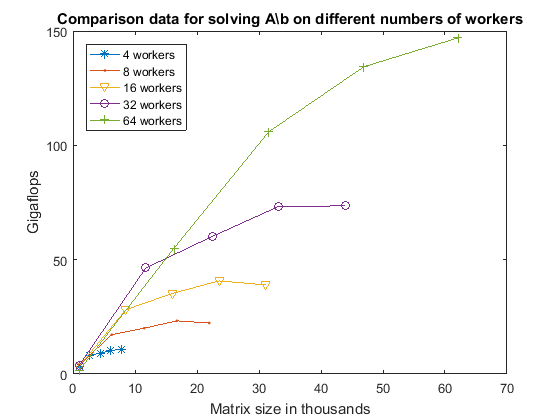
当我们查看上面的图时，我们首先注意到的是，与仅使用 4 个工作单元相比，64 个工作单元使我们能够解决更大的线性方程组。此外，我们可以看到，即使可以使用 4 个工作单元来处理大小为 60,000×60,000 的矩阵，我们也只能获得大约 10 Gigaflops 的性能。因此，即使 4 个工作单元拥有足够的内存来解决如此大的问题，64 个工作单元的表现仍将远远优于它们。

观察 4 个工作单元的曲线斜率，我们可以看到，三个最大矩阵规模之间的性能仅有适度提升。将其与之前不同矩阵大小下 A\b 的预期性能图进行比较，我们得出结论，对于 4 个工作单元来说，我们非常接近实现矩阵大小为 7772×7772 的峰值性能。

查看 8 个和 16 个工作单元的曲线，我们可以看到，随着矩阵规模的增大，性能会下降，这表明我们接近或已经耗尽了可用的系统内存。然而，我们发现第二大和第三大矩阵大小之间的性能提升非常适中，表明了某种稳定性。因此，我们推测，当使用 8 个或 16 个工作单元时，如果我们增加系统内存并使用更大的矩阵大小进行测试，我们很可能不会看到 Gigaflops 的显著增加。

查看 32 和 64 个工作单元的曲线，我们发现第二大和第三大矩阵规模之间的性能有显著的提升。对于 64 个工作单元来说，两个最大矩阵规模之间的性能也有显著的提升。因此，我们推测，在达到峰值性能之前，32 和 64 个工作单元的系统内存就会耗尽。如果这是正确的，那么给计算机增加更多的内存既可以让我们解决更大的问题，又可以在更大的矩阵规模下获得更好的性能。

加速

测量反斜杠等线性代数算法获得的加速比的传统方法是比较峰值性能。因此，我们计算出每个工作单元所能达到的最大 Gigaflops 数量。

peakPerf = [max(s.workers4.gflops), max(s.workers8.gflops), ...
            max(s.workers16.gflops), max(s.workers32.gflops), ...
            max(s.workers64.gflops)];
disp('Peak performance in Gigaflops for 4-64 workers:')
disp(peakPerf)

disp('Speedup when going from 4 workers to 8, 16, 32 and 64 workers:')
disp(peakPerf(2:end)/peakPerf(1))

Peak performance in Gigaflops for 4-64 workers:
   10.9319   23.2508   40.7157   73.5109  147.0693

Speedup when going from 4 workers to 8, 16, 32 and 64 workers:
    2.1269    3.7245    6.7244   13.4532

因此，我们得出结论，当工作单元数量增加 16 倍（从 4 个工作单元增加到 64 个工作单元）时，速度将提高约 13.5 倍。正如我们上面提到的，性能图表明，通过增加集群计算机上的系统内存，我们可能能够提高 64 个工作单元的性能（从而进一步提高加速）。

使用的集群

这些数据是使用 16 台双处理器、八核计算机生成的，每台计算机配备 64 GB 内存，并通过千兆以太网连接。当使用 4 个工作单元时，它们都在一台计算机上。我们为 8 个工作单元配备 2 台计算机，为 16 个工作单元配备 4 台计算机，等等。

重新启用死锁检测

现在我们已经完成了基准测试，我们可以安全地重新启用当前并行池中的死锁检测。

pctRunOnAll 'mpiSettings(''DeadlockDetection'', ''on'');'

end

ans = 

  struct with fields:

    matSize: [1000 19787 38573 57360 76146]
     gflops: [1.1618 43.7417 69.6855 40.4145 36.9379]

基准测试 A\ b