任务并行问题中的资源争用
这个示例说明了为什么很难对“我的并行代码在我的多核计算机或集群上的表现如何?”这个问题给出一个具体的答案。
最常见的答案是“这取决于您的代码和硬件”,这个示例将尝试解释为什么无需更多信息就能说出这些。
此示例使用在同一多核 CPU 上的工作单元上运行的并行代码,并强调了内存访问争用的问题。为了简化问题,此示例对您的计算机执行不涉及磁盘 IO 的任务并行问题的能力进行了基准测试。这使您可以忽略可能影响并行代码执行的几个因素,例如:
进程间通信量
进程间通信的网络带宽和延迟
进程启动和关闭时间
将请求分发到进程的时间
磁盘 IO 性能
只剩下:
执行任务并行代码所花费的时间
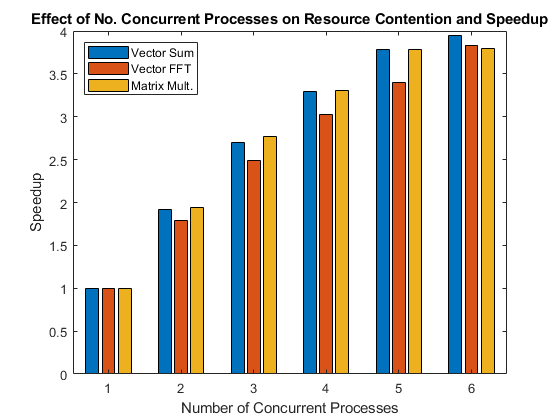
该图显示了在多个并发进程中并行执行操作时实现的加速。
资源竞争与效率的类比
要理解为什么值得执行这样一个简单的基准测试,请考虑以下示例:如果一个人可以在一分钟内装满一桶水,将它扛到一段距离,然后倒空,再带回来再装满水,那么两个人每人带着一个桶走同样的往返路程需要多长时间?这个简单的类比密切反映了本示例中的任务并行基准。乍一看,两个人同时做同一件事相对于一个人做而言效率会有所降低,这似乎很荒谬。
争夺一根水管:资源争用
如果我们之前的示例中的所有事情都很完美,那么两个人在一分钟内各自用一桶水完成一圈。每个人快速地装满一个桶,把桶带到目的地,然后清空桶并走回来,并且确保彼此之间不会互相干扰或打扰。
然而,想象一下他们必须用一根小水管来往水桶里注水。如果他们同时到达水管,则必须等待。这是共享资源争用的一个示例。也许两个人不需要同时使用水管,因此水管可以满足他们的需要;但如果有 10 个人每人运送一个水桶,有些人可能总是需要等待。
类比中,水管对应于计算机硬件,特别是内存。如果多个程序在每个 CPU 核心上同时运行,并且它们都需要访问存储在计算机内存中的数据,则由于内存带宽有限,某些程序可能需要等待。
相同软管,不同距离,不同结果
想象一下,当两个人每人提着一个桶时,在水管处发生争抢,但随后任务发生了变化,人们必须将水抬到离水管更远的地方。在执行这项修改后的任务时,两个人花费更多的时间来做工作(即带着水桶走路),而花费更少的时间来争夺共享资源(水管)。因此它们不太可能同时需要水管,所以这个修改后的任务比原来的任务具有更高的并行效率。
就此示例中的基准测试而言,一方面这对应于运行需要大量访问计算机内存的程序,但是它们对获取的数据执行的操作却很少。另一方面,如果程序对数据执行大量计算,那么获取数据所花费的时间就变得无关紧要,计算时间将超过等待访问内存的时间。
算法的内存访问的可预测性也会影响内存访问的竞争程度。如果以有规律的、可预测的方式访问内存,则争用将比以不规则的方式访问内存时少。下面可以进一步看到这一点,例如,奇异值分解计算比矩阵乘法导致更多的争用。
启动并行池
关闭所有现有的并行池并使用 parpool 启动基于进程的并行池。使用默认设置,parpool 在本地计算机上启动一个池,每个物理 CPU 核心一个工作单元,最多不超过 Processes' 配置文件中设置的限制。
delete(gcp("nocreate")); % Close any existing parallel pools p = parpool("Processes");
Starting parallel pool (parpool) using the 'Processes' profile ... Connected to the parallel pool (number of workers: 6).
poolSize = p.NumWorkers;
计时函数
本示例末尾提供了一个计时函数 timingFcn。计时函数在 spmd 语句内执行五次函数,并保留给定并发级别观察到的最短执行时间。
如上所述,此示例对任务并行问题进行了基准测试,仅测量实际运行时间。这意味着该示例不会对 MATLAB®、Parallel Computing Toolbox™ 或 spmd 语言构造的性能进行基准测试。相反,该示例对操作系统和硬件同时运行程序的多个副本的能力进行了基准测试。
建立基准测试问题
创建一个足够大的输入矩阵,以便每次处理时都需要将其从计算机内存转移到 CPU 上。也就是说,使其足够大以引起资源争用。
sz = 2048; m = rand(sz*sz,1);
求和运算
本示例末尾提供了对单个数组 sumOp 执行重复求和的函数。由于求和运算在计算上是轻量的,因此在使用大型输入数组同时运行此函数的多个副本时,您可能会看到资源争用。因此,您应该预计,在同时执行多个此类评估时,评估求和函数所需的时间将比在空闲 CPU 上执行单个此类评估所需的时间更长。
快速傅里叶变换运算
本示例末尾提供了对向量 fftOp 执行重复快速傅里叶变换 (FFT) 的函数。FFT 运算比求和运算的计算量更大,因此,在同时评估对 FFT 函数的多个调用时,您应该不会看到与对求和函数的调用相同的性能下降。
矩阵乘法运算
本示例末尾提供了执行矩阵乘法的函数 multOp。矩阵乘法中的内存访问非常有规律,因此该运算有可能在多核计算机上非常高效并行执行。
调查资源争用
测量对 N 个工作单元同时评估 N 个求和函数需要多长时间,N 的值从 1 到并行池的大小。
tsum = timingFcn(@() sumOp(m), 1:poolSize);
Execution times: 0.279930, 0.292188, 0.311675, 0.339938, 0.370064, 0.425983
测量在 N 个工作单元上同时评估 N 个 FFT 函数需要多长时间,其中 N 的值从 1 到并行池的大小。
tfft = timingFcn(@() fftOp(m),1:poolSize);
Execution times: 0.818498, 0.915932, 0.987967, 1.083160, 1.205024, 1.280371
测量在 N 个工作单元上同时评估 N 个矩阵乘法函数需要多长时间,其中 N 的值从 1 到并行池的大小。
m = reshape(m,sz,sz); tmtimes = timingFcn(@() multOp(m),1:poolSize);
Execution times: 0.219166, 0.225956, 0.237215, 0.264970, 0.289410, 0.346732
clear m将计时结果合并到一个数组中,并计算通过同时运行多个函数调用所实现的加速。
allTimes = [tsum(:), tfft(:), tmtimes(:)]; speedup = (allTimes(1,:)./allTimes).*((1:poolSize)');
将结果绘制在条形图中。该图显示了所谓的弱扩展带来的加速。弱扩展是指进程/处理器的数量会发生变化,而每个进程/处理器上的问题规模是固定的。随着进程/处理器数量的增加,这会导致总体问题规模也随之增加。另一方面,强扩展是指问题规模固定,而进程/处理器的数量变化。其结果是,随着进程/处理器数量的增加,每个进程/处理器所做的工作就会减少。
bar(speedup) legend('Vector Sum', 'Vector FFT', 'Matrix Mult.', ... 'Location', 'NorthWest') xlabel('Number of Concurrent Processes'); ylabel('Speedup') title(['Effect of No. Concurrent Processes on ', ... 'Resource Contention and Speedup']);

对实际应用的影响
查看上面的图,您会发现问题在同一台计算机上可能会出现不同的扩展。考虑到其他问题和计算机可能表现出非常不同的行为,应该清楚为什么不可能对“我的(并行)应用程序在我的多核计算机或集群上的表现如何?”这个问题给出一个一般性的答案。这个问题的答案确实取决于相关的应用程序和硬件。
衡量数据大小对资源争用的影响
资源争用不仅取决于正在执行的函数,还取决于正在处理的数据的大小。为了说明这一点,您将测量具有不同大小的输入数据的各种函数的执行时间。与之前一样,您正在测试硬件同时执行这些计算的能力,而非 MATLAB 或其算法。将考虑比以前更多的函数,以便您可以研究不同内存访问模式的影响以及不同数据大小的影响。
定义数据大小并指定测试中使用的操作。
szs = [128, 256, 512, 1024, 2048];
operations = {'Vector Sum', 'Vector FFT', 'Matrix Mult.', 'Matrix LU', ...
'Matrix SVD', 'Matrix EIG'};循环遍历不同的数据大小和函数,并测量并行池中所有工作单元的连续执行时间和并发执行所需的时间。
speedup = zeros(length(szs), length(operations)); % Loop over the data sizes for i = 1:length(szs) sz = szs(i); fprintf('Using matrices of size %d-by-%d.\n', sz, sz); j = 1; % Loop over the different operations for f = [{@sumOp; sz^2; 1}, {@fftOp; sz^2; 1}, {@multOp; sz; sz}, ... {@lu; sz; sz}, {@svd; sz; sz}, {@eig; sz; sz}] op = f{1}; nrows = f{2}; ncols = f{3}; m = rand(nrows, ncols); % Compare sequential execution to execution on all workers tcurr = timingFcn(@() op(m), [1, poolSize]); speedup(i, j) = tcurr(1)/tcurr(2)*poolSize; j = j + 1; end end
Using matrices of size 128-by-128.
Execution times: 0.000496, 0.000681 Execution times: 0.001933, 0.003149 Execution times: 0.000057, 0.000129 Execution times: 0.000125, 0.000315 Execution times: 0.000885, 0.001373 Execution times: 0.004683, 0.007004
Using matrices of size 256-by-256.
Execution times: 0.001754, 0.002374 Execution times: 0.012112, 0.022556 Execution times: 0.000406, 0.001121 Execution times: 0.000483, 0.001011 Execution times: 0.004097, 0.005329 Execution times: 0.023690, 0.033705
Using matrices of size 512-by-512.
Execution times: 0.008338, 0.018826 Execution times: 0.046627, 0.089895 Execution times: 0.003986, 0.007924 Execution times: 0.003566, 0.007190 Execution times: 0.040086, 0.081230 Execution times: 0.185437, 0.261263
Using matrices of size 1024-by-1024.
Execution times: 0.052518, 0.096353 Execution times: 0.235325, 0.339011 Execution times: 0.030236, 0.039486 Execution times: 0.022886, 0.048219 Execution times: 0.341354, 0.792010 Execution times: 0.714309, 1.146659
Using matrices of size 2048-by-2048.
Execution times: 0.290942, 0.407355 Execution times: 0.855275, 1.266367 Execution times: 0.213512, 0.354477 Execution times: 0.149325, 0.223728 Execution times: 3.922412, 7.140040 Execution times: 4.684580, 7.150495
绘制在池中的所有工作单元上针对每个数据大小同时运行时每个操作的加速情况,显示理想的加速情况。
figure
ax = axes;
plot(speedup)
set(ax.Children, {'Marker'}, {'+', 'o', '*', 'x', 's', 'd'}')
hold on
plot([1 length(szs)],[poolSize poolSize], '--')
xticks(1:length(szs));
xticklabels(szs + "^2")
xlabel('Number of Elements per Process')
ylim([0 poolSize+0.5])
ylabel('Speedup')
legend([operations, {'Ideal Speedup'}], 'Location', 'SouthWest')
title('Effect of Data Size on Resource Contention and Speedup')
hold off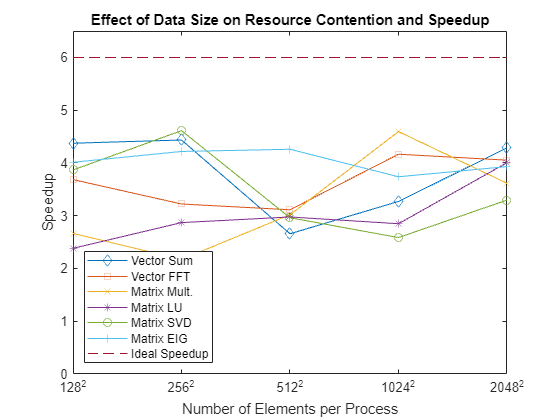
查看结果时,请记住函数如何与 CPU 上的缓存交互。对于小数据量,您总是使用 CPU 缓存来执行所有这些函数。在这种情况下,您可以期待看到良好的加速。当输入数据太大而无法放入 CPU 缓存时,您会开始看到因内存访问争用而导致的性能下降。
支持函数
计时函数
timingFcn 函数接受一个函数句柄和多个并发进程。对于并发进程数 N,该函数测量在 spmd 代码块内使用 N 个并行工作单元执行 N 次函数句柄所代表的函数时的执行时间。
function time = timingFcn(fcn, numConcurrent) time = zeros(1,length(numConcurrent)); numTests = 5; % Record the execution time on 1 to numConcurrent workers for ind = 1:length(numConcurrent) n = numConcurrent(ind); spmd(n) tconcurrent = inf; % Time the function numTests times, and record the minimum time for itr = 1:numTests % Measure only task parallel runtime spmdBarrier; tic; fcn(); % Record the time for all to complete tAllDone = spmdReduce(@max, toc); tconcurrent = min(tconcurrent, tAllDone); end end time(ind) = tconcurrent{1}; clear tconcurrent itr tAllDone if ind == 1 fprintf('Execution times: %f', time(ind)); else fprintf(', %f', time(ind)); end end fprintf('\n'); end
求和函数
函数 sumOp 对输入矩阵执行 100 次求和运算并累积结果。为了获得准确的时间,进行了 100 次求和运算。
function sumOp(m) s = 0; for itr = 1:100 s = s + sum(m); end end
FFT 函数
函数 fftOp 对输入数组执行 10 次 FFT 运算。为了获得准确的时间,进行了 10 次 FFT 运算。
function fftOp(m) for itr = 1:10 fft(m); end end
矩阵乘法函数
函数 multOp 将输入矩阵与其自身相乘。
function multOp(m) m*m; end
另请参阅
parpool | spmd | spmdBarrier | spmdReduce