尝试并行计算方法

自 R2025a 起

此示例展示了如何使用并行计算来加速您的 MATLAB® 代码。尝试示例，了解如何在 MATLAB 中开始使用并行计算。

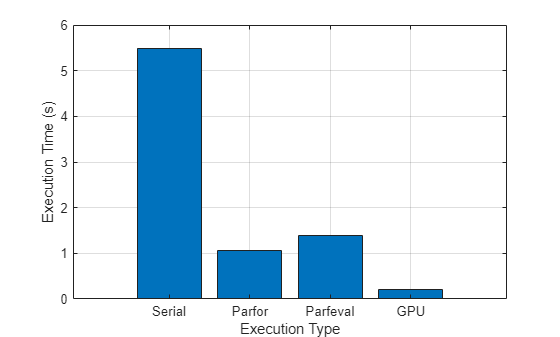
该图表显示了在运行本示例所用算法时，三种并行计算方法与串行计算相比的执行时间。您的结果将取决于您的硬件配置。

Bar graph showing the execution times for three parallel computing methods compared to serial computing when running the algorithm used in this example.

开发算法

首先，对算法进行原型设计。在此示例中，您使用 computePi 函数运行蒙特卡罗算法来估计 $π$ 的值。

该算法执行以下步骤：

随机生成 $m$ 个包含 $x$ - 和 $y$ - 坐标的集合，坐标范围为 [0,1]。
判断给定的坐标是否描述了一个位于单位正方形内圆上的点。
重复步骤 1 和 2， $n$ 次。
使用圆中的点数和点总数来计算 $π$ 的估计值。

有关使用蒙特卡罗算法估算 $π$ 的更多详细信息，请参阅简单蒙特卡罗面积方法部分。

创建蒙特卡罗算法。

function piEst = computePi(m,n)
pointsInCircle = 0;

for i = 1:n
    % Generate random points.
    x = rand(m,1);
    y = rand(m,1);

    % Determine whether the points lie inside the unit circle.
    r = x.^2 + y.^2;
    pointsInCircle = pointsInCircle + sum(r<=1);
end

piEst = 4/(m*n) * pointsInCircle;
end

检查算法是否计算出一个合理的估计值。

m  = 3e5;
n  = 1e3;

piEst = computePi(m,n)

piEst = 
3.1415

使用 timeit 函数来测量运行 computePi 函数所需的时间。

timeSerial = timeit(@() computePi(m,n))

timeSerial = 
5.4936

尝试并行处理方法

您可以使用并行处理来加速此算法。在本节中，您将对代码进行微小的更改，使其使用三种并行计算方法运行。然后，您评估哪种并行处理方法最适合加速算法。

Parfor 方法

如果算法中包含 for 循环，且迭代顺序无关紧要，则将 for 循环转换为 parfor 循环通常是并行化代码的最简单方法。

定义一个新函数 computePiParfor，该函数使用 parfor 循环代替 for 循环来估计 $π$ 。

function piEst = computePiParfor(m,n)
pontsInCircle = 0;

parfor i = 1:n
    % Generate random points.
    x = rand(m,1);
    y = rand(m,1);

    % Determine whether the points lie inside the unit circle.
    r = x.^2 + y.^2;
    pontsInCircle = pontsInCircle + sum(r<=1);
end

piEst = 4/(m*n) * pontsInCircle;
end

启动基于线程的并行池。默认情况下，MATLAB 在本地计算机上以每个物理内核一个工作单元的方式启动一个池。

pool = parpool("Threads");

Starting parallel pool (parpool) using the 'Threads' profile ...
Connected to parallel pool with 6 workers.

测量运行 computePiParfor 函数所需的时间。

timeParfor = timeit(@() computePiParfor(m,n))

timeParfor = 
1.0548

使用 parfor 循环可以显著加快算法运行速度，且对代码的修改极少。

Parfeval 方法

您可以使用 parfeval 在并行工作单元上运行一个函数。

定义一个函数 calculatePoints，该函数生成 $m$ 个随机点，并判断这些点是否位于单位圆内。此函数对应于原始 computePi 函数中的 for 循环的单次迭代。

function pointsInCircle = calculatePoints(m)
% Generate random points.
x = rand(m,1);
y = rand(m,1);

% Determine whether the points lie inside the unit circle.
r = x.^2 + y.^2;
pointsInCircle = sum(r<=1);
end

定义一个函数 computePiParfeval，用于根据 parfeval 估计 $π$ 。此函数在 for 循环中调用 parfeval，在并行池中的工作单元上执行 calculatePoints 函数 $n$ 次。该函数随后使用这些结果来生成 $π$ 的估计值。每个工作单元都有一个独立的随机数流，因此对 rand 的调用会在每个工作单元上产生一组唯一的随机数序列。有关在工作单元中控制随机数生成的详细信息，请参阅控制工作单元上的随机数流。

function piEst = computePiParfeval(m,n)

for i = 1:n
    f(i) = parfeval(@calculatePoints,1,m);
end

output  = fetchOutputs(f);
piEst = 4/(m*n) * sum(output);
end

测量运行 computePiParfeval 函数所需的时间。

timeParfeval = timeit(@() computePiParfeval(m,n))

timeParfeval = 
1.3845

从时间安排可以看出，parfeval 不适合当前的问题，因为 calculatePoints 函数运行太快，导致通信和调度开销过大。然而，parfeval 特别适合解决那些已知预期结果但未知需要多少次迭代才能达到该结果的问题。例如，如果您想迭代优化一个估计值 $π$ ，直到解决方案不再改进，您可以使用 parfeval 来排队 10,000 次迭代，当目标达到时，您可以取消所有剩余的迭代。一个改进的函数，用于计算 $π$ ，使用 parfeval 和 computePiParfevalImproved，已作为支持文件附加到此示例中。打开此示例作为实时脚本以访问支持文件。

GPU 方法

如果您拥有支持的 GPU，您可以通过在 GPU 上运行代码来加速您的程序。有关支持的 GPU 的更多信息，请参阅 GPU 计算要求。

gpu = gpuDevice;
disp(gpu.Name + " GPU selected.")

NVIDIA RTX A5000 GPU selected.

定义一个新函数 computePiGPU，用于在 GPU 上估计 $π$ 。如果您提供 gpuArray 数据参量，MATLAB 和其他工具箱中的许多函数都会在 GPU 上自动运行。computePiGPU 函数生成随机点并以 gpuArray 数据格式输出，随后相关计算将自动在 GPU 上执行。

function piEst = computePiGPU(m,n)
c = zeros(1,"gpuArray");

for i = 1:n
    % Generate random points on the GPU.
    x = rand(m,1,"gpuArray");
    y = rand(m,1,"gpuArray");

    % Determine whether the points lie inside the unit circle.
    r = x.^2 + y.^2;
    c = c + sum(r<=1);
end

piEst = 4/(m*n) * c;
end

使用 gputimeit 函数来测量运行 computePiGPU 函数所需的时间。对于使用 GPU 的函数，gputimeit 函数优于 timeit，因为它确保在记录时间之前所有 GPU 操作已完成，并补偿了额外开销。

timeGPU = gputimeit(@() computePiGPU(m,n))

timeGPU = 
0.2079

您可以通过将 for 循环向量化，进一步在 GPU 上加速此代码。向量化是将基于循环的代码修改为使用矩阵和向量运算的过程。向量化代码在运行于 GPU 的加速代码中特别有效，因为 GPU 在执行大量操作时通常更高效。一个改进的函数，使用向量化代码在 GPU 上计算 $π$ ，即 computePiGPUVectorized，已作为支持文件附在此示例中。打开此示例作为实时脚本以访问支持文件。

比较执行时间

比较并行方法与串行执行的执行时间。

figure
bar([timeSerial timeParfor timeParfeval timeGPU])
xlabel("Execution Type")
xticklabels(["Serial" "Parfor" "Parfeval" "GPU"])
ylabel("Execution Time (s)")
grid on

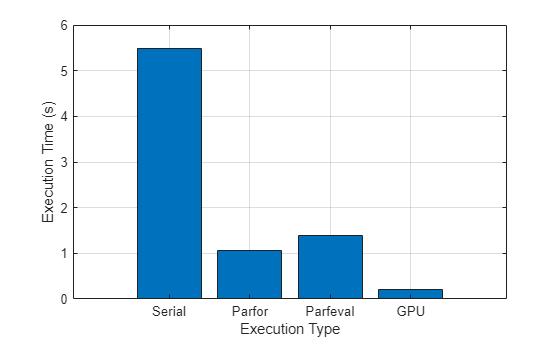
在运行本示例中的算法时，三种并行计算方法的执行时间明显快于串行计算。您的结果将取决于您的硬件配置。

简单蒙特卡罗面积方法

给定一个半径为 $r$ 的圆内切于一个边长为 $2 r$ 的正方形，该圆的面积与正方形的面积之比为 $π$ 。该图很能说明问题。

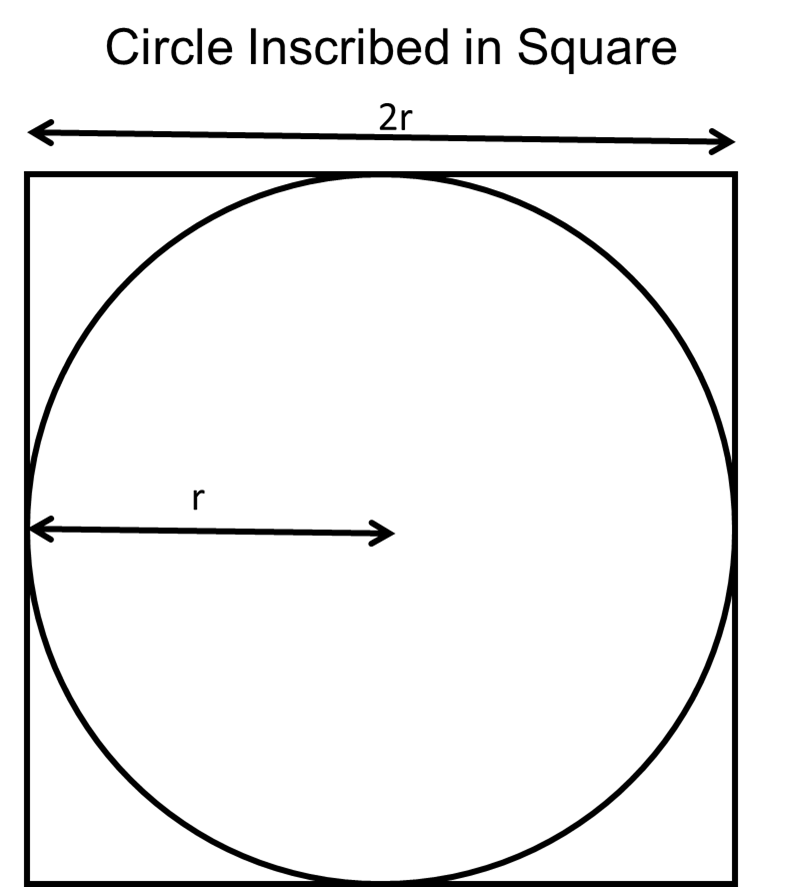
您可以通过圆的面积与正方形的面积之比推导出 $π$ ：

$\frac{area of circle}{area of square} =$

$\frac{π r^{2}}{{(2 r)}^{2}} = \frac{π}{4}$

要估算圆的面积而不直接使用 $π$ ，可以随机生成一个均匀分布在正方形内部的点样本，然后统计其中有多少个点位于圆内。在圆中找到一个点的概率是圆的面积除以正方形的面积之比。

要确定一个点是否在圆内，随机生成该点的 $x$ - 和 $y$ - 坐标的两个值，并计算该点与圆原点的距离。从原点到生成点的距离 $d$ 由以下方程给出：

$d = \sqrt{x^{2} + y^{2}}$

如果 $d$ 小于圆的半径 $r$ ，则该点位于圆内。生成大量点样本并计算圆内有多少个点。使用此数据来获取圆内的点与生成的总点数的比例。这个比率相当于圆的面积与正方形的面积之比。然后，您可以使用以下方法估算 $π$ ：

$\frac{points in circle}{total number of points} \approx \frac{π}{4}$

$π \approx 4 \times \frac{points in circle}{total number of points}$

另请参阅

parfor | parfeval | gpuArray