assempde

Partial Differential Equation Toolbox™ solves equations of the form

When the m and d coefficients are 0, this reduces to

which the documentation calls an elliptic equation, whether or not the equation is elliptic in the mathematical sense. The equation holds in Ω, where Ω is a bounded domain in two or three dimensions. c, a, f, and the unknown solution u are complex functions defined on Ω. c can also be a 2-by-2 matrix function on Ω. The boundary conditions specify a combination of u and its normal derivative on the boundary:

$$\overrightarrow{n}$$ is the outward unit normal. g, q, h, and r are functions defined on ∂Ω.

Our nomenclature deviates slightly from the tradition for potential theory, where a Neumann condition usually refers to the case q = 0 and our Neumann would be called a mixed condition. In some contexts, the generalized Neumann boundary conditions is also referred to as the Robin boundary conditions. In variational calculus, Dirichlet conditions are also called essential boundary conditions and restrict the trial space. Neumann conditions are also called natural conditions and arise as necessary conditions for a solution. The variational form of the Partial Differential Equation Toolbox equation with Neumann conditions is given below.

The approximate solution to the elliptic PDE is found in three steps:

More elaborate applications make use of the Finite Element Method (FEM) specific information returned by the different functions of the software. Therefore we quickly summarize the theory and technique of FEM solvers to enable advanced applications to make full use of the computed quantities.

FEM can be summarized in the following sentence: Project the weak form of the differential equation onto a finite-dimensional function space. The rest of this section deals with explaining the preceding statement.

We start with the weak form of the differential equation. Without restricting the generality, we assume generalized Neumann conditions on the whole boundary, since Dirichlet conditions can be approximated by generalized Neumann conditions. In the simple case of a unit matrix h, setting g = qr and then letting q → ∞ yields the Dirichlet condition because division with a very large q cancels the normal derivative terms. The actual implementation is different, since the preceding procedure may create conditioning problems. The mixed boundary condition of the system case requires a more complicated treatment, described in Systems of PDEs.

Assume that u is a solution of the differential equation. Multiply the equation with an arbitrary test function v and integrate on Ω:

Integrate by parts (i.e., use Green's formula) to obtain

The boundary integral can be replaced by the boundary condition:

Replace the original problem with Find u such that

This equation is called the variational, or weak, form of the differential equation. Obviously, any solution of the differential equation is also a solution of the variational problem. The reverse is true under some restrictions on the domain and on the coefficient functions. The solution of the variational problem is also called the weak solution of the differential equation.

The solution u and the test functions v belong to some function space V. The next step is to choose an Np-dimensional subspace $$V_{N_p}\subset V$$. Project the weak form of the differential equation onto a finite-dimensional function space simply means requesting u and v to lie in $$V_{N_p}$$ rather than V. The solution of the finite dimensional problem turns out to be the element of $$V_{N_p}$$ that lies closest to the weak solution when measured in the energy norm. Convergence is guaranteed if the space $$V_{N_p}$$ tends to V as N_p→∞. Since the differential operator is linear, we demand that the variational equation is satisfied for N_p test-functions Φ_i ∊$$V_{N_p}$$ that form a basis, i.e.,

Expand u in the same basis of $$V_{N_p}$$ elements

and obtain the system of equations

Use the following notations:

and rewrite the system in the form

K, M, and Q are N_p-by-N_p matrices, and F and G are N_p-vectors. K, M, and F are produced by assema, while Q, G are produced by assemb. When it is not necessary to distinguish K, M, and Q or F and G, we collapse the notations to KU = F, which form the output of assempde.

When the problem is self-adjoint and elliptic in the usual mathematical sense, the matrix K + M + Q becomes symmetric and positive definite. Many common problems have these characteristics, most notably those that can also be formulated as minimization problems. For the case of a scalar equation, K, M, and Q are obviously symmetric. If c(x) ≥ δ > 0, a(x) ≥ 0 and q(x) ≥ 0 with q(x) > 0 on some part of ∂Ω, then, if U ≠ 0.

U^T(K + M + Q)U is the energy norm. There are many choices of the test-function spaces. The software uses continuous functions that are linear on each element of a 2-D mesh, and are linear or quadratic on elements of a 3-D mesh. Piecewise linearity guarantees that the integrals defining the stiffness matrix K exist. Projection onto $$V_{N_p}$$ is nothing more than linear interpolation, and the evaluation of the solution inside an element is done just in terms of the nodal values. If the mesh is uniformly refined, $$V_{N_p}$$ approximates the set of smooth functions on Ω.

A suitable basis for $$V_{N_p}$$ in 2-D is the set of “tent” or “hat” functions ϕ_i. These are linear on each element and take the value 0 at all nodes x_j except for x_i. For the definition of basis functions for 3-D geometry, see Finite Element Basis for 3-D. Requesting ϕ_i(x_i) = 1 yields the very pleasant property

That is, by solving the FEM system we obtain the nodal values of the approximate solution. The basis function ϕ_i vanishes on all the elements that do not contain the node x_i. The immediate consequence is that the integrals appearing in K_i,j, M_i,j, Q_i,j, F_i and G_i only need to be computed on the elements that contain the node x_i. Secondly, it means that K_i,j andM_i,j are zero unless x_i and x_j are vertices of the same element and thus K and M are very sparse matrices. Their sparse structure depends on the ordering of the indices of the mesh points.

The integrals in the FEM matrices are computed by adding the contributions from each element to the corresponding entries (i.e., only if the corresponding mesh point is a vertex of the element). This process is commonly called assembling, hence the name of the function assempde.

The assembling routines scan the elements of the mesh. For each element they compute the so-called local matrices and add their components to the correct positions in the sparse matrices or vectors.

The discussion now specializes to triangular meshes in 2-D. The local 3-by-3 matrices contain the integrals evaluated only on the current triangle. The coefficients are assumed constant on the triangle and they are evaluated only in the triangle barycenter. The integrals are computed using the midpoint rule. This approximation is optimal since it has the same order of accuracy as the piecewise linear interpolation.

Consider a triangle given by the nodes P₁, P₂, and P₃ as in the following figure.

The simplest computations are for the local mass matrix m:

where P_c is the center of mass of Δ P₁P₂P₃, i.e.,

The contribution to the right side F is just

For the local stiffness matrix we have to evaluate the gradients of the basis functions that do not vanish on P₁P₂P₃. Since the basis functions are linear on the triangle P₁P₂P₃, the gradients are constants. Denote the basis functions ϕ₁, ϕ₂, and ϕ₃ such that ϕ(P_i) = 1. If P₂ – P₃ = [x₁,y₁]^T then we have that

and after integration (taking c as a constant matrix on the triangle)

If two vertices of the triangle lie on the boundary ∂Ω, they contribute to the line integrals associated to the boundary conditions. If the two boundary points are P₁ and P₂, then we have

and

where P_b is the midpoint of P₁P₂.

For each triangle the vertices P_m of the local triangle correspond to the indices i_m of the mesh points. The contributions of the individual triangle are added to the matrices such that, e.g.,

This is done by the function assempde. The gradients and the areas of the triangles are computed by the function pdetrg.

The Dirichlet boundary conditions are treated in a slightly different manner. They are eliminated from the linear system by a procedure that yields a symmetric, reduced system. The function assempde can return matrices K, F, B, and ud such that the solution is u = Bv + ud where Kv = F. u is an N_p-vector, and if the rank of the Dirichlet conditions is rD, then v has N_p – rD components.

To summarize, assempde performs the following steps to obtain a solution u to an elliptic PDE:

assempde uses one of two algorithms for assembling a problem into combined finite element matrix form. A reduced linear system form leads to immediate solution via linear algebra. You choose the algorithm by the number of outputs. For the reduced linear system form, request four outputs:

For the stiff-spring approximation, request two outputs:

For details, see Reduced Linear System and Stiff-Spring Approximation.

Partial Differential Equation Toolbox software can also handle systems of N partial differential equations over the domain Ω. We have the elliptic system

the parabolic system

the hyperbolic system

and the eigenvalue system

where c is an N-by-N-by-D-by-D tensor, and D is the geometry dimensions, 2 or 3.

For 2-D systems, the notation $$\nabla \cdot (c\otimes \nabla u)$$ represents an N-by-1 matrix with an (i,1)-component

For 3-D systems, the notation $$\nabla \cdot (c\otimes \nabla u)$$ represents an N-by-1 matrix with an (i,1)-component

The symbols a and d denote N-by-N matrices, and f denotes a column vector of length N.

The elements c_ijkl, a_ij, d_ij, and f_i of c, a, d, and f are stored row-wise in the MATLAB matrices c, a, d, and f. The case of identity, diagonal, and symmetric matrices are handled as special cases. For the tensor c_ijkl this applies both to the indices i and j, and to the indices k and l.

Partial Differential Equation Toolbox software does not check the ellipticity of the problem, and it is quite possible to define a system that is not elliptic in the mathematical sense. The preceding procedure that describes the scalar case is applied to each component of the system, yielding a symmetric positive definite system of equations whenever the differential system possesses these characteristics.

The boundary conditions now in general are mixed, i.e., for each point on the boundary a combination of Dirichlet and generalized Neumann conditions,

For 2-D systems, the notation $$n·\left(c\otimes \nabla u\right)$$ represents an N-by-1 matrix with (i,1)-component

where the outward normal vector of the boundary is $$n=\left(\cos (\alpha ),\sin (\alpha )\right)$$.

For 3-D systems, the notation $$n·\left(c\otimes \nabla u\right)$$ represents an N-by-1 matrix with (i,1)-component

where the outward normal to the boundary is

There are M Dirichlet conditions and the h-matrix is M-by-N, M ≥ 0. The generalized Neumann condition contains a source $$h^{\prime }\mu$$, where the Lagrange multipliers μ are computed such that the Dirichlet conditions become satisfied. In a structural mechanics problem, this term is exactly the reaction force necessary to satisfy the kinematic constraints described by the Dirichlet conditions.

The rest of this section details the treatment of the Dirichlet conditions and may be skipped on a first reading.

Partial Differential Equation Toolbox software supports two implementations of Dirichlet conditions. The simplest is the “Stiff Spring” model, so named for its interpretation in solid mechanics. See Elliptic Equations for the scalar case, which is equivalent to a diagonal h-matrix. For the general case, Dirichlet conditions

are approximated by adding a term

to the equations KU = F, where L is a large number such as 10⁴ times a representative size of the elements of K.

When this number is increased, hu = r will be more accurately satisfied, but the potential ill-conditioning of the modified equations will become more serious.

The second method is also applicable to general mixed conditions with nondiagonal h, and is free of the ill-conditioning, but is more involved computationally. Assume that there are N_p nodes in the mesh. Then the number of unknowns is N_pN = N_u. When Dirichlet boundary conditions fix some of the unknowns, the linear system can be correspondingly reduced. This is easily done by removing rows and columns when u values are given, but here we must treat the case when some linear combinations of the components of u are given, hu = r. These are collected into HU = R where H is an M-by-N_u matrix and R is an M-vector.

With the reaction force term the system becomes

The constraints can be solved for M of the U-variables, the remaining called V, an N_u – M vector. The null space of H is spanned by the columns of B, and U = BV + u_d makes U satisfy the Dirichlet conditions. A permutation to block-diagonal form exploits the sparsity of H to speed up the following computation to find B in a numerically stable way. µ can be eliminated by pre-multiplying by B´ since, by the construction, HB = 0 or B´H´ = 0. The reduced system becomes

which is symmetric and positive definite if K is.

The finite element method for 3-D geometry is similar to the 2-D method described in Elliptic Equations. The main difference is that the elements in 3-D geometry are tetrahedra, which means that the basis functions are different from those in 2-D geometry.

It is convenient to map a tetrahedron to a canonical tetrahedron with a local coordinate system (r,s,t).

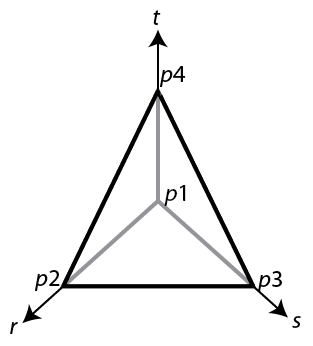
In local coordinates, the point p1 is at (0,0,0), p2 is at (1,0,0), p3 is at (0,1,0), and p4 is at (0,0,1).

For a linear tetrahedron, the basis functions are

For a quadratic tetrahedron, there are additional nodes at the edge midpoints.

The corresponding basis functions are

As in the 2-D case, a 3-D basis function ϕ_i takes the value 0 at all nodes j, except for node i, where it takes the value 1.

assempde is not recommended. Use solvepde instead. There are no plans to remove assempde.